Abstract
Filtered backprojection (FBP) algorithms reduce image noise by smoothing the image. Iterative algorithms reduce image noise by noise weighting and regularization. It is believed that iterative algorithms are able to reduce noise without sacrificing image resolution, and thus iterative algorithms, especially maximum-likelihood expectation maximization (MLEM), are used in nuclear medicine to replace FBP algorithms. Methods: This short paper uses counter examples to show that this belief is not true. We compare image noise variance for FBP and MLEM reconstructions having the same spatial resolution. Results: The truth is that although MLEM suppresses image noise, it does so by sacrificing image resolution as well; the performance of windowed FBP may be better than that of MLEM in our case study. Conclusion: The myth of the superiority of iterative algorithms is caused by comparing them with conventional FBP instead of with windowed FBP. However, we do not intend to generalize the comparison results to imply which algorithm is more favorable.
- tomography
- image reconstruction
- iterative image reconstruction
- emission tomography
- analytic image reconstruction
Iterative algorithms are widely used in emission and transmission image reconstruction. A clear reason to choose an iterative algorithm over the filtered backprojection (FBP) algorithm is the superior noise reduction performance of the former over the latter (1–3). FBP reduces image noise by applying a low-pass filter, which causes some spatial resolution loss. On the other hand, iterative algorithms do not, in general, use a low-pass filter to suppress noise. Instead, they use the weighting factors according to the noise variance and regularization to control noise.
Many research groups have compared FBP with iterative algorithms in nuclear medicine image reconstruction (4–7). Both types of algorithm have advantages and disadvantages. Because there is no embedded low-pass filter in iterative algorithms, they are expected to reduce image noise without sacrificing image resolution. If compared with FBP, for a given image resolution, iterative algorithms are expected to produce an image that is less noisy.
Research on FBP has been relatively quiet in recent years. In contrast, research on iterative algorithms has been active—for example, research on generating a more accurate system matrix, developing more computationally efficient methods, and producing more stable solutions (8–12).
By applying maximum-likelihood expectation maximization (MLEM) as an example of the iterative algorithm, this paper uses counter examples to show that the advantages of MLEM over FBP are a myth and that MLEM suppresses image noise, but only by sacrificing image resolution as well. If we compare the results of MLEM with those of windowed FBP, these 2 algorithms can be seen to perform similarly in terms of noise and resolution. MLEM may not have clear advantages. However, we do not intend to generalize the comparison results to imply which algorithm is more favorable.
MATERIALS AND METHODS
In this paper, MLEM and windowed FBP are used to demonstrate noise performance at different image resolutions. These 2 algorithms control noise using 2 different methods. MLEM uses different numbers of iterations to regulate noise. FBP uses different low-pass filters to filter out noise. It will be shown that image resolution is affected regardless of the method used to reduce noise.
MLEM
The MLEM considered in this paper has the following form (13,14):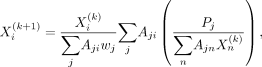
Eq. 1
where 
is the ith image pixel at the kth iteration, 
is the jth line-integral (ray-sum) measurement value, and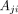 
is the contribution of the ith image pixel to the jth measurement. The summation over the index n is the projector, and the summation over the index j is the backprojector.
FBP
Noise-weighted FBP (also known as windowed FBP) was developed to model and suppress noise (15,16). This algorithm emulates the gradient descent algorithm and contains a control index k, which is similar to the iteration number in MLEM. This windowed FBP is almost the same as conventional FBP, except for the ramp filter. In conventional FBP, the ramp filter is |ω|, where ω is the frequency discretely sampled from −0.5 to 0.5. In windowed FBP, the ramp filter is modified by a window function and is expressed as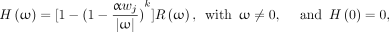
Eq. 2
where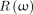 
is a ramp filter and α is a positive constant to prevent the algorithm from divergence. In this paper, α is set to 0.0001. Equation 2 can be factored as a ramp filter 
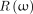and a window function 
. In practice, there are many versions of ramp filter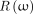 
associated with various fixed window functions, such as a rectangular function (also known as the Ram–Lak filter), a sinc function (also known as the Shepp–Logan filter), a raised cosine function, a Hamming function, a Hann function, and so on. In addition to the variable window function 
, we use the raised cosine function as a fixed window for the ramp filter. Precisely, the version of the ramp filter used in this paper is expressed as
Eq. 3
The implementation of Equation 2 is in the Fourier domain of the sinogram. The weighting factors wj in Equation 2 for all projection bins are quantized into 11 discrete values, and each of these 11 quantized weighting factors produces a filtered sinogram. A combined sinogram from these filtered sinograms is formed point-by-point according to the variance of the original sinogram. The details of the implementation have been previously published (9).
We use the notation α in Equation 2 to represent the step size. The effect of step size α in Equation 2 can be clearly understood from the published derivation (9). The notation k in Equation 2 represents the iteration number. The effect of iteration number k in Equation 2 can be seen from the published derivation (9) as well. When MLEM reaches a certain image contrast, it stops at iteration k. However, for windowed FBP, the image contrast is controlled by the product of αk. To prevent divergence, the parameter α must be very small. This parameter α can be fixed. Once α is fixed, the image contrast is determined only by the parameter k.
Computer Simulations
A computer-generated National Electrical Manufacturers Association NU 4-2008 image-quality phantom (17) was used for the simulation studies. The phantom is circular and contains 5 hot lesions of different sizes. The lesions are used for spatial resolution evaluation. The details of the phantom are given in Table 1 using the MATLAB (The MathWorks, Inc.) phantom format, where the units for the first 4 columns are the relative dimension with respect to the array size, and the unit for the last column is the photon counts. Noiseless projections are calculated analytically without using pixel discretization. The projection noise is incorporated after the noiseless line-integrals are generated.
Parameters (Fractions of Image Size) for National Electrical Manufacturers Association NU 4-2008 Phantom
This paper considers a 2-dimensional parallel-beam imaging system with a flat 1-dimensional detector. The detector has 180 detection channels (i.e., detection bins), and the projections are simulated at 180 views over 360°. The image is reconstructed in a 180 × 180 array. The noise for each projection ray is Poisson-distributed, as in an emission imaging system. In this model, the noise-weighting factor is the reciprocal of the measurement and the weighting factor is incorporated in windowed FBP. The Poisson noise is naturally modeled in MLEM.
The simulation studies are in 2 steps. In the first step, the noiseless projections are used to reconstruct the image with 5, 10, 15, 20, 25, 30, 35, 40, and 45 iterations with MLEM. By comparing the line profiles horizontally across the center of each lesion, the matching parameter, k, as defined in Equation 2 is found for windowed FBP. The parameters k in Equation 2 that correspond to iterations 5, 10, 15, 20, 25, 30, 35, 40, and 45 in MLEM are 3,800, 8,200, 12,000, 17,000, 22,000, 28,000, 33,000, 38,000, and 43,000, respectively.
In the second step, the noisy projections are used, and the images are reconstructed in pairs. The uniform nonzero background region within the phantom is used to calculate image noise.
RESULTS
The noiseless reconstruction pairs are shown in Figure 1, where pairs of windowed FBP reconstructions and MLEM reconstructions are matched in terms of spatial resolution. The reconstructed image pairs using noisy data are shown in Figures 1–2. The line profiles shown are drawn from the corresponding reconstructions with noiseless data. The 5 line-profiles drawn horizontally across the center of the 5 lesions are pieced together and displayed in a single box. The noise in a nonzero uniform background region within a rectangular shape is calculated as SD divided by the mean value (i.e., the normalized SD). These normalized SDs are summarized in Table 2.
Left image is reconstructed with 5 iterations of MLEM. Middle image is reconstructed with windowed FBP with k = 3,800. Right image is same as middle image except outside object image values are set to zero. Line profiles are for 5 lesions. Solid lines are from windowed FBP images; dashed lines are from MLEM images.
Left image in each panel is reconstructed with various iterations of MLEM. Middle image is reconstructed with windowed FBP with various value of k. Right image is same as middle image except outside object image values are set to zero. Line profiles are for 5 lesions. Solid lines are from windowed FBP images; dashed lines are from MLEM images. (A) Left: 10 iterations; middle: k = 8,200. (B) Left: 15 iterations; middle: k = 12,000. (C) Left: 20 iterations; middle: k = 17,000. (D) Left: 25 iterations; middle: k = 22,000. (E) Left: 30 iterations; middle: k = 28,000. (F) Left: 35 iterations; middle: k = 33,000. (G) Left: 40 iterations; middle: k = 38,000. (H) Left: 45 iterations; middle: k = 43,000.
Noise Comparison for Reconstructions with MLEM and Windowed FBP, When Images Are at Same Lesion Contrast
Because the uniform regions in the image are not uniform at lower iterations, the image reconstructed with noisy data is normalized by the image reconstructed with noiseless data with the same parameters, such as the iteration number.
The images reconstructed with windowed FBP are displayed twice. In one display, the images are displayed at full scale, from the image global minimum to maximum. In the second display, the near-zero image values outside the object are set to zero. MLEM does not allow negative image values, whereas FBP does. The second display shows greater comparability between the images reconstructed using the 2 algorithms.
For the same spatial resolution, MLEM images are slightly noisier than windowed FBP images for the chosen window functions. However, if some other window functions are used, the MLEM images can be less noisy than the windowed FBP images (not shown). We do not generalize our results to claim which algorithm is better, because the results vary with different window functions, object shapes, and noise levels. This paper presents only a counter example.
DISCUSSION
When the iteration number is small, only lower-frequency components are included in the reconstructed image. As the iteration number increases, higher-frequency components are included in the image. Thus, image resolution is directly related to the iteration number.
MLEM is a nonlinear algorithm, whereas windowed FBP is linear. They behave differently. Equation 2 shows that the role of the noise-weighting factor wj is to modify the step size α in windowed FBP. A larger step size α is equivalent to more iterations. A smaller step size α is equivalent to fewer iterations. Since the iteration number is directly related to the spatial resolution, the step size is also directly related to the spatial resolution. A smaller step size corresponds to a lower resolution.
After the weighting factors wj are introduced to FBP, the effective step size is αwj. As a consequence, a smaller weighting factor wj corresponds to a lower resolution. In other words, applying a small weighting factor wj to a projection ray pj is equivalent to applying a low-pass filter to pj. For the noisier projections, smaller weighting factors are assigned—equivalent to smoothing these projections with a low-pass filter.
It is safe to state that MLEM suppresses noise by smoothing, which degrades image resolution. Therefore, it is an unfounded myth that MLEM can reduce noise without sacrificing image resolution whereas FBP gives poorer resolution if noise is to be suppressed. The myth is caused by comparison of MLEM with conventional FBP instead of with windowed FBP. If we compare the MLEM results with the windowed FBP results, these 2 algorithms perform similarly in terms of noise and resolution. MLEM may not have clear advantages.
The performance of both MLEM and windowed FBP can be further improved by incorporating some a priori information, which is sometimes referred to as Bayesian reconstruction (a topic that is beyond the scope of this paper).
In noiseless data simulation studies, images reconstructed by many iterative algorithms show high-frequency noise when the iteration number is extremely high. This image noise is caused by pixelization of the image array, in which the image is represented by flat, square pixels. The pixilated-image projection cannot exactly match the analytically generated projection. This discrepancy causes the high-frequency noise in the image. Interestingly, this noise is not observed in FBP reconstruction.
CONCLUSION
This paper has presented some counter examples to show that MLEM and windowed FBP have similar noise-versus-resolution trade-offs. For image reconstruction in modern-day nuclear medicine practice, the use of MLEM and its accelerated versions has almost replaced the use of FBP for 2 reasons: the general belief that iterative algorithms can handle noise better than FBP, and the ability of an iterative algorithm to perform nonuniform attenuation correction, especially in SPECT. Our paper can positively affect the first aspect. Windowed FBP handles noise equally as well as MLEM. The significant advantage of windowed FBP is its fast reconstruction time, which is clinically important especially for PET, with its large datasets and lengthy reconstructions using iterative algorithms.
Windowed FBP currently cannot correct for nonuniform attenuation in SPECT. In PET, attenuation can be corrected in the sinogram domain, and windowed FBP can thus be used for reconstruction. We believe that time-of-flight and detector response modeling can be handled by a noniterative algorithm, but this issue is beyond our present scope and would require future development. This work focuses mainly on image noise issues in nuclear medicine imaging.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Footnotes
Published online Feb. 2, 2018.
REFERENCES
- Received for publication May 22, 2017.
- Accepted for publication December 20, 2017.
Jump to section
Related Articles
Cited By...
- No citing articles found.