Research ArticleImaging

A Monte Carlo Study of the Dependence of Early Frame Sampling on Uncertainty and Bias in Pharmacokinetic Parameters from Dynamic PET

Ida Häggström, Jan Axelsson, Charles Ross Schmidtlein, Mikael Karlsson, Anders Garpebring, Lennart Johansson, Jens Sörensen and Anne Larsson
Journal of Nuclear Medicine Technology March 2015, 43 (1) 53-60; DOI: https://doi.org/10.2967/jnmt.114.141754

Abstract

Compartmental modeling of dynamic PET data enables quantification of tracer kinetics in vivo, through the calculated model parameters. In this study, we aimed to investigate the effect of early frame sampling and reconstruction method on pharmacokinetic parameters obtained from a 2-tissue model, in terms of bias and uncertainty (SD). Methods: The GATE Monte Carlo software was used to simulate 2 × 15 dynamic 3′-deoxy-3′-18F-fluorothymidine (18F-FLT) brain PET studies, typical in terms of noise level and kinetic parameters. The data were reconstructed by both 3-dimensional (3D) filtered backprojection with reprojection (3DRP) and 3D ordered-subset expectation maximization (OSEM) into 6 dynamic image sets with different early frame durations of 1, 2, 4, 6, 10, and 15 s. Bias and SD were evaluated for fitted parameter estimates, calculated from regions of interest. Results: The 2-tissue-model parameter estimates K1, k2, and fraction of arterial blood in tissue depended on early frame sampling, and a sampling of 6–15 s generally minimized bias and SD. The shortest sampling of 1 s yielded a 25% and 42% larger bias than the other schemes, for 3DRP and OSEM, respectively, and a parameter uncertainty that was 10%–70% higher. The schemes from 4 to 15 s were generally not significantly different in regards to bias and SD. Typically, the reconstruction method 3DRP yielded less frame-sampling dependence and less uncertain results, compared with OSEM, but was on average more biased. Conclusion: Of the 6 sampling schemes investigated in this study, an early frame duration of 6–15 s generally kept both bias and uncertainty to a minimum, for both 3DRP and OSEM reconstructions. Very-short frames of 1 s should be avoided because they typically resulted in the largest parameter bias and uncertainty. Furthermore, 3DRP may be preferred over OSEM for short frames with poor statistics.

PET is a widely used and powerful tool for the quantitative in vivo study of radiolabeled molecules (tracers). In quantitative PET imaging, it is important to understand and quantify random (uncertainty) and systematic (bias) errors that will affect the quantitative information within an image set. Although there have been many studies focused on the bias and uncertainty of model parameter estimates (1,2), the effect of the early frame duration on these quantities is less understood.

Many early studies regarding optimal frame-sampling schedules are mainly focused on the blood assay sampling for input function determination or reducing the computational time and storage space of dynamic image sets (3–6). Raylman et al. (7) studied protocols for dynamic cardiac imaging with different early frame samplings from 60 down to 5 s and concluded that the first 100 s of the acquisition have to be sampled at 5 or 10 s for an acceptable bias in K1 and k2 for the 1-tissue-compartment model. Jovkar et al. (8) investigated schemes with the first 3 min sampled at combinations of 10, 30, and 60 s and found that parameter SD decreased with decreased frame sampling (down to 10 s).

These studies included only frame-sampling intervals down to 10 s, or occasionally 5 s, however. Moreover, the studies used calculated time–activity curves (TACs) and either used the theoretic TACs directly or, to resemble real clinical data, added noise according to a Poisson or gaussian distribution. Although the noise in projection data (sinograms) is Poisson distributed, the distribution is usually much more complex after the reconstruction process, especially for nonlinear iterative reconstruction algorithms (9,10). To avoid making assumptions and simplifications regarding the camera system blurring effect and noise distribution on the PET image level, a more sophisticated simulation method is needed. By using Monte Carlo (MC) techniques, one can obtain images with realistic noise distributions and proper camera system effects.

The 18F-labeled molecule FDG (18F-FDG) is the most commonly used PET tracer in general and for tumor imaging in particular (11). Other tracers, however, such as 3′-deoxy-3′-18F-fluorothymidine (18F-FLT), have proven successful alternatives to 18F-FDG for brain tumor studies (11–14). This work focused on the tracer 18F-FLT, which can be used to image tumor proliferation (11–14).

In dynamic PET, the tracer distribution over time is observed. The collected projection data are sorted into frames from which the kinetics of the tracer in a tissue or organ of interest can be quantified. Commonly, the dynamic data are analyzed using a tracer-specific compartment model, yielding a set of model-determined parameters representing the tracer kinetics. For dynamic PET imaging, list-mode data can be collected and binned to arbitrary frame durations. When reconstructing the data into a dynamic image set, the user is faced with the choice of using longer frames with better counting statistics but poor temporal resolution or shorter frames with poor counting statistics but better temporal resolution.

Short frames may be of interest during the first minutes of the dynamic PET study to better capture the fast variations in the tracer uptake and clearance, which are usually largest for early frames, and for a better definition of the early blood peak (6). This is especially true for image-derived TACs of the blood, because they are sharper than the TACs of the tissue and thus require higher sampling rates (7). Clinical PET frames are often sampled at intervals ranging from 10 to 300 s, although frames shorter than 5 s exist but are rare. Although short frames are often desired in dynamic PET imaging, they are seldom used because of the poor statistics associated with short frames and poor quality and bias of image reconstructions of such frames (6).

The aim of this study was to investigate the effects different sampling schemes (frame durations) for early frames have on pharmacokinetic parameter estimates in regards to bias and SD for typical dynamic 18F-FLT brain studies with typical dose administrations (noise level). The aim was also to investigate the effect of the reconstruction method used for the dynamic PET data by comparing the results for analytic 3-dimensional (3D) filtered backprojection with reprojection (3DRP) and 3D ordered-subset expectation maximization (OSEM). In order to obtain data, the MC software GATE was used to simulate 2 × 15 separate dynamic PET studies with a digital head phantom with added tumors, representing 18F-FLT with realistic kinetic parameter values.

MATERIALS AND METHODS

Compartment Model

The 2-tissue-compartment model seen in Figure 1 is commonly used to describe 18F-FLT (15). The TAC describing the activity concentration in arterial blood plasma is known as the input function Cp, and the 2 TACs describing the tissue concentrations, CF + NS and CS, represent free-plus-nonspecific (nondisplaceable) and specifically bound tracer in tissue, respectively. The model parameters that govern the tracer exchange are the uptake rate from blood to nondisplaceable tracer in tissue K1 (mL cm−3 min−1), the clearance rate from nondisplaceable tracer in tissue k2 (min−1), and the rates between the nondisplaceable and specifically bound tracer tissue compartments k3 (min−1) and k4 (min−1), respectively. Va (mL cm−3) is the fraction of arterial blood in tissue. The influx rate constant Ki (mL cm−3 min−1) is commonly used when evaluating dynamic data and is defined as (8,12,15):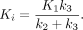Embedded ImageEq. 1

FIGURE 1.
FIGURE 1.

2-tissue-compartment model consisting of compartments of arterial blood plasma (Cp), free-plus-nonspecific (nondisplaceable) and specifically bound tracer in tissue (CF + NS and CS), 4 rate constants (K1, k2, k3, k4), and tissue blood fraction (Va). CPET is the apparent concentration in a PET image VOI or voxel.

The activity measured by the PET camera is the sum of CF + NS and CS, plus an added blood component to account for signal contamination from blood vessels within the voxel or a volume of interest (VOI) (8,16,17).

Monte Carlo Simulation

GATE (18) was used to perform MC simulations of 3D dynamic PET 18F-FLT brain scans. The camera simulated was a previously validated Discovery LS PET scanner (GE Healthcare) (19), consisting of 18 detection rings with 672 bismuth germanate crystals of approximately 4 × 8 × 30 mm each. The transaxial field of view was 550 mm, and the axial field of view 152 mm.

The phantom used in the simulations was the voxelized digital BrainWeb head phantom (20). The phantom was simulated and described in a previous study (21) and is briefly described here. The phantom consisted of 7 main materials, with 7 uniform spheric tumors (diameters, 3, 6, 9, 12, 18, 24, and 30 mm) distributed in each hemisphere (14 inserted tumors). Finally, a 25-mm spheric blood region was placed centrally in the brain. The constructed phantom had an isotropic voxel size of 1 × 1 × 1 mm and is depicted in Figure 2. The size, shape, and location of the blood region was designed to be practical for extraction of an image-derived input function of small variance and little influence of partial-volume effects, rather than to be realistic. Furthermore, the inclusion of a blood region within the phantom eliminated the need for additional simulations (e.g., the heart) for input-function derivation.

FIGURE 2.
FIGURE 2.

Voxelized BrainWeb head phantom, with inserted spheric blood and tumor regions, labeled with their diameter in mm. All tissues were attributed realistic TACs, and the blood region was assigned the input function (Cp) and all 14 tumor regions the same TTAC (CPET).

Realistic pharmacokinetics were assigned to all normal phantom tissues, and fitted TACs from 2 clinical dynamic brain 18F-FLT scans performed at Umeå University Hospital were used for those regions. The same input function Cp was assigned to the blood region in both setups, denoted FLT1 and FLT2. Cp was generated using Matlab (version 8.1.0; The MathWorks Inc.) and had a typical input function appearance (22), with a realistic peak amplitude of around 50 kBq/mL3 (measured at Umeå University Hospital). For each of the 2 setups, Matlab was used to generate the corresponding tissue TAC (TTAC) CPET, according to the 2-tissue model with the realistic 18F-FLT parameter values for gliomas, seen in Table 1 (12,13). For both FLT1 and FLT2, all 14 tumor regions were assigned the same TTAC CPET. The simulated blood and tumor TACs are seen in Figure 3. The source particles simulated were 18F positrons with an electron range production cut of 2 mm, a δ-ray production cut of 10 keV, and an x-ray production cut of 10 keV (19,23). Physical decay of the sources was applied with a half-life of 6,586.2 s. The activities in the tissue and blood regions of the phantom were read from the generated TACs and updated every second of the simulation. For practical reasons, the detector dead time was not included in the simulation. The total GATE acquisition time was set to 60 min, and simulated data were stored in list-mode. Thirty MC simulations were performed: 15 of the setup with FLT1 and 15 with FLT2, to improve the statistics for the kinetic parameter analyses. Although simulated, the random coincidences were not included in the study. The effect of random coincidences was considered small because the random fraction for the 2 setups was merely 2%.

View this table:
TABLE 1

2 Sets of Simulated 18F-FLT Parameter Values: FLT1 (12) and FLT2 (13)

FIGURE 3.
FIGURE 3.

Common input function Cp and CPET for the two 18F-FLT parameter sets, showing the activity concentration for the blood and tumor regions, respectively.

As previously described by Häggström et al. (21), data from 1 normalization and 1 calibration simulation were also used for the image reconstruction normalization and quantitative calibration.

All simulations were performed using the computer cluster Akka (Intel Xeon quad-core L5420 central processing units) at the HPC2N collaboration, Umeå University. Each of the 30 dynamic simulations required about 3,300 central-processing unit hours.

Image Reconstruction

The list-mode true plus scattered coincidences were binned into 3D sinograms (19) and reconstructed using 2 methods: analytic 3DRP (24) and OSEM (25) iterative reconstruction. The reconstructions were performed using the software STIR (26). A Colsher filter (cutoff frequency, 0.5 pixel−1) was applied for 3DRP, and the OSEM settings were chosen so that the tumor VOI values had reached convergence at 60 subiterations and 12 subsets (5 iterations). Both methods had normalization, decay, attenuation, and scatter corrections applied.

For the attenuation correction, a linear attenuation coefficient data map (μ-map) relevant for 511-keV photons for the respective phantom materials was generated from the BrainWeb phantom. The normalization simulation data were binned into a sinogram to create the normalization sinogram (27). A scatter sinogram estimate was created from the single scatter simulation algorithm implemented in STIR (28,29) and used as additive sinograms in the OSEM loop. Attenuation and normalization data were also included in the loop, whereas all 3 corrections were used as precorrections for 3DRP.

In accordance with clinical settings of the Discovery LS (GE Healthcare), all reconstructed images were postfiltered with a gaussian transverse filter of 6.0 mm in full width at half maximum and a 3-point smoothing filter [1 2 1]/4 in the axial direction. Reconstructed image sizes were 165 × 165 × 35 voxels, with a voxel size of 2 × 2 × 4.25 mm.

Finally, a scale factor to calibrate all images from counts to Bq/mL was created from a 3DRP reconstruction of the true coincidences from the calibration simulation.

The dynamic PET data were reconstructed into 6 dynamic image sets, with the first 2 min (covering the early blood peak) sampled at 120 × 1, 60 × 2, 30 × 4, 20 × 6, 12 × 10, or 8 × 15 s. The PET data between 2 and 60 min were all sampled at 2 × 30, 2 × 60, 2 × 150, and 10 × 300 s.

Model Fitting and Parameter Analysis

The input function was image-derived from a spheric VOI covering the complete blood region (25-mm diameter, 488 voxels, 8.3 mL), and 2 tumor TTACs from each simulation were derived from complete VOIs of the largest left and right tumors, respectively (30-mm diameter, 843 voxels, 14.3 mL). In this study, only the 2 largest 30-mm tumors were used to minimize partial-volume effects (the additional 12 tumor spheres are intended for another study). The data used for analysis thus comprised 15 input functions and 2 TTACs per input function, making a total of 30 tumor TTACs for each of FLT1 and FLT2, for which the TAC values were calculated as the mean value of the VOI at each frame.

Kinetic parameter estimates were obtained by nonlinear least-squares (NLS) fitting of each of the TTACs with the input function considered a noiseless model input. The NLS fitting is commonly weighted, and each TTAC value should be weighted according to its inverse variance. Because the true variance is typically unknown, it is usually approximated by considering radioactive decay, frame duration, and often also frame count. However, weighting according to noisy counts can degrade the parameter estimation severely (30,31). Furthermore, in order not to force a fit only to the last few TTAC values with long frame durations and in essence ignore the short early frames, a uniform weight was used for all frames in this study. The Matlab function lsqnonlin was used for the fitting, and the true values were used as start values to avoid any effects from the choice of initial parameter guesses. The mid time of each frame was used as the time point, and the influx rate parameter Ki was calculated according to Equation 1 for each VOI.

The 30 sets of kinetic parameters were finally averaged into 1 single set of estimated [K1, k2, k3, k4, Va, Ki] for each of the 6 sampling schemes, for both FLT1 and FLT2. The relative bias of all 6 pharmacokinetic parameter estimates P was calculated as:Embedded ImageEq. 2where Embedded Image is the true parameter value. The accompanying relative SE in the bias wasEmbedded ImageEq. 3where Embedded Image is the SD of parameter estimate P. The relative SD in the parameter estimates was calculated according toEmbedded ImageEq. 4

The theoretic, noiseless input functions and TTACs, resampled to match the 6 different frame-sampling schemes, were also NLS-fitted and compared with the results from the image-derived TACs.

The obtained biases were analyzed with 1- and 2-way ANOVA tests, followed by post hoc Bonferroni pairwise tests to make out individual differences between reconstruction methods and sampling schemes. Results with a p-value of less than 0.05 were considered significant.

All data fitting and analyses were performed in Matlab.

RESULTS

On average, the total registered and kept coincidences from the 15 simulations was 119 × 106 and 137 × 106, for FLT1 and FLT2, respectively. The total kcounts per frame for the early frames (first 120 s) of the different sampling schemes are seen in Table 2.

View this table:
TABLE 2

Total Number of kcounts in the Early Frames (First 120 Seconds of Acquisition) for the Different Sampling Schemes

Examples of the reconstructed images are seen in Figure 4, and representative TTACs from 1 of the 30 FLT1 tumor VOIs, with corresponding NLS fit, are seen in Figure 5. As can be seen in both figures, the noise level of the images and subsequent TACs decrease as the frame duration increases. The calculated bias and SD of the parameter estimates from the NLS fits of the image-derived input function and TTAC are seen in Figure 6, and the results for the resampled theoretic (noiseless) TAC (nonclinical case used merely for comparison) are seen in Figure 7.

FIGURE 4.
FIGURE 4.

Example images from the FLT1 study, for the different early frame-sampling schemes plus true phantom image. The frame around 120 s is presented, and the early frame durations are indicated in the columns of figure.

FIGURE 5.
FIGURE 5.

Representative example from first 20 min of FLT1 study, showing OSEM. TTACs and corresponding NLS fits for 6 different early frame-sampling schemes are shown.

FIGURE 6.
FIGURE 6.

Relative error (bias) (A) and uncertainty (SD) (B) in all parameter estimates for 6 different early frame-sampling schemes. Error bars in bias represent SE. y-axes are scaled differently for better visibility.

FIGURE 7.
FIGURE 7.

Relative bias for all model parameters for the 6 different early frame-sampling schemes, using the resampled theoretic (noiseless) input function and TTAC for the NLS fit.

The shortest early sampling of 1 s generally produced the most biased parameter estimates, and more so for OSEM, compared with 3DRP reconstructions. On average, the 1-s parameter bias magnitudes were 25% and 43% larger than the other sampling schemes, for 3DRP and OSEM, respectively. Because of parameter uncertainties, however, the results were only significant for parameters K1, k2, and Va with OSEM (both FLT setups), K1 and k2 for FLT2 with 3DRP, and Va for both FLT setups with 3DRP. The 2-s scheme also yielded significantly larger biases than the longer schemes for parameters K1 and k2 with OSEM. In general, the sampling schemes of 4, 6, 10, and 15 s did not differ significantly, with the exception of Va with 3DRP, for which most schemes differed from one another. From Figure 7 (theoretic, noiseless TACs), it is apparent that Va is the parameter most dependent on frame sampling.

On average, parameter k3 was the least biased estimate at 4% on average for all schemes and 3% when excluding the 1-s scheme. Its bias from 2- to 15-s sampling was in fact not significantly different from the theoretic case at around 2%.

The minimum bias magnitude was found between 6- and 15-s early frame sampling for both FLT setups for all 6 parameters and both reconstruction methods. The minimum typically occurred at a shorter sampling of 6 s for 3DRP and about 15 s for OSEM. However, the schemes of 4, 6, 10, and 15 s were generally not significantly different.

Parameter estimate uncertainties (SDs) were generally stable for an early frame sampling of 2–15 s but increased by 10%–70% when shortening it to 1 s. The uncertainty was smallest for parameter K1, with an average of 4%, and largest for k4 at 25%.

When the significant results of the 2 reconstruction methods were compared, 3DRP produced more biased estimates of K1, k2, and Va than OSEM, by 44%, 92%, and 314%, respectively, and a less biased k4 by 8%. Uncertainties, however, were larger for OSEM reconstructions by on average 15%.

DISCUSSION

In this study, we investigated the effect of early frame duration on bias and SD in pharmacokinetic parameter estimates obtained from the 2-tissue-compartment model for typical 18F-FLT brain studies.

Two sets of kinetic parameter value sets were chosen, representing the tracer 18F-FLT, but because the simulations themselves were parameter-specific, not tracer-specific, the results are likely valid for any tracer suited for the 2-tissue-compartment model with similar pharmacokinetic parameter values and noise level (dose administration). Two image reconstruction methods were also studied, 3DRP and OSEM.

Of the statistically significant results, the bias was generally smallest for early frame durations of 6–15 s. A frame-sampling dependence was generally found for K1, k2,Va, and more so for OSEM than 3DRP. The closer statistical analysis revealed that it was the 1-s, and occasionally also the 2-s, scheme that stood out from the rest. With 3DRP, it was only for the faster kinetics described by FLT2 that a frame-sampling dependence was found for K1 and k2. The slower kinetics in FLT1 did not show a significant sampling dependence. These results are not surprising because faster kinetics should intuitively be more prone to undersampling than slower kinetics for which the TACs do not vary as quickly from frame to frame. Parameter K1 mainly governs the amplitude of the TTAC, whereas k2, k3, and k4 together contribute to the shape of the TTAC. This makes predictions regarding individual parameter responses to changes in the TTAC shape difficult. Apart from the highest bias, the SDs were also highest for the shortest frames of 1 s, which is expected because the signal-to-noise ratio of the frames is roughly proportional to the square root of the number of counts.

The bias for OSEM appeared to have a frame duration dependence, which was more pronounced than for 3DRP, for parameters K1 and k2. It is known that iterative reconstruction (OSEM) of low-count images may result in (positively) biased images whereas analytic reconstruction methods (3DRP) do not (32,33). The bias introduced due to low count reconstruction may explain the larger bias for short frames and hence more prominent frame duration dependence for OSEM, compared with 3DRP. The parameter K1, which mainly controls the peak amplitude of the TTAC, would thus be most affected by a biased ROI value. Compared with OSEM, 3DRP images have a high background noise and streak artifacts (Fig. 4). However, the lowest-count OSEM images (1- and 2-s frames) appear to have artifacts in the form of high uptake spots. The effect of the low count bias for short framed OSEM images and how it transfers to the parameter biases and SDs is hard to include properly in studies in which the TACs are simulated directly with added noise profiles. This effect is more realistically depicted using full MC simulations with complete image reconstructions.

Furthermore, according to typical practice, the same setting (here 60 subiterations, 12 subsets) was used for all frame-sampling schemes and for all frames of each scheme. However, because of the difference in statistics between the different frames, they should ideally (despite practicality issues) have the OSEM reconstruction settings optimized individually. Furthermore, OSEM images have noisier hot regions than 3DRP, and vice versa for cold regions, as known from literature (9,34). Cerebellum VOI (cold) SDs and tumor VOI (hot) SDs were on average 71% higher and 28% lower, respectively, when 3DRP was compared with OSEM. This fact, together with the low count bias, may explain the 15% larger parameter uncertainties obtained for OSEM than 3DRP images. However, the noise level in OSEM images is heavily dependent on the number of iterations, and other reconstruction settings could yield slightly different results.

It is apparent that Va is dependent on the frame duration. Even the theoretic TACs (Fig. 7) resulted in large biases for the longer sampling intervals. Because Va is determined by the early blood peak seen in the TTAC, a long frame duration will effectively lower the peak due to smearing and cause an underestimated Va. An input function with a wider peak would most likely decrease the frame-sampling dependence and yield less bias in Va. On the other hand, a more narrow blood peak would likely cause Va to be more underestimated.

Both k3 and Ki were found independent of early frame sampling. Even though Figure 6 shows a larger bias for the shortest 1-s frame sampling, the results were not significant. These 2 parameters have been shown to be of potentially larger clinical value (13,14), so a small dependence on frame-sampling scheme is desired. Because Ki is a macroparameter calculated from 3 other parameters, it is likely to be more stable than single parameters (6). The image-derived k3 was not different from the theoretic noiseless case. Thus, the effects of, for example, the camera system blurring and reconstruction process did not add additional bias to the estimate, making k3 reliable and strengthening its role as a clinically relevant parameter.

The bias and SD of parameter k4 were large. A longer scan time (>60 min) would likely improve the k4 estimation (15), but as this parameter is rarely considered clinically important because of large uncertainties, we chose not to take this into further consideration. Jovkar et al. (8) found that keeping k4 fixed in the fitting procedure resulted in more stable estimates of all other parameters.

According to our findings, noise and bias in the image-derived TACs can affect the parameter uncertainty and bias to a large extent. Because the input function is derived from only 1 ROI and assumed true for the fitting procedure, any bias in it will affect all parameter estimates. If the chosen blood ROI is not representative, the calculated bias and SD in the parameter estimates may be largely affected. To minimize uncertainty and bias, the use of a population-based input function might be helpful (22,35). However, the population-based input function is subject to interpatient variability and may be biased in itself.

The parameter bias was found larger for 3DRP than OSEM and the uncertainty smaller on average. As shown by Thiele et al. (31) and Yaqub et al. (30), the choice of weight factors for weighted NLS can affect the results to a relatively large extent. In addition to uniform weighting, the fitting and subsequent parameter analyses were also done with 2 standard weight estimations (31) (data not shown). For the ith frame in each set, the 2 weights wi were calculated as: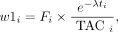Embedded ImageEq. 5andEmbedded ImageEq. 6where Fi is the frame duration, ti the frame mid time, λ the decay constant, and TACi the TAC value of the ith frame. The results when including either of the weights were on average worse than with uniform weighting. We therefore chose not to present these results. However, although we found OSEM to produce less biased parameter estimates when using uniform weighting, when either w1 or w2 was used, 3DRP yielded considerably better estimates than OSEM. The bias for OSEM reconstructions benefited from uniform weighting, whereas 3DRP showed minimum bias for w1.

The size of the tumor ROIs were set to 14.3 mL in this study, which is a realistic volume for a brain tumor ROI. The ROI size and the image noise level (activity) will affect the results because a larger ROI or higher activity yields better statistics. In this study, the focus was to evaluate a typical 18F-FLT study and administered dose (noise level), and kinetic parameter values were chosen accordingly. For a more general understanding of the parameter biases and uncertainties in relation to noise level and pharmacokinetics, a full range of different dose administrations and parameter value sets could be simulated and analyzed.

Finally, when FLT1 and FLT2 are compared, it is clear that the magnitudes of both bias and SD are often different, reflecting the difference in parameter reliability on the individual patient level as there is a wide range of clinically possible kinetic parameter values.

CONCLUSION

In general for this study, an early frame sampling of 6–15 s was found to minimize the overall bias in pharmacokinetic parameters for both 3DRP and OSEM reconstructions. Parameters K1, k2, and Va showed a statistically significant frame-sampling dependence, with the largest bias for the shortest frames of 1 s and more so for OSEM, compared with 3DRP. The parameter uncertainties were generally stable for frames of 2–15 s but higher for the short 1-s sampling.

The estimation of k3 was most reliable (bias < 5% in general), and the parameter Va was overall most dependent on frame duration.

Despite the visually more appealing OSEM images, the analytic image reconstruction method 3DRP showed less dependence on early frame sampling, compared with the iterative technique OSEM. Moreover, OSEM reconstructions of the shortest early frames (1 and 2 s) had artifacts in the form of high uptake spots, not seen in the 3DRP images.

DISCLOSURE

The costs of publication of this article were defrayed in part by the payment of page charges. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734. This work was supported in part by the Swedish Cancer Society and the Cancer Research Foundation at Umeå University. No other potential conflict of interest relevant to this article was reported.

Acknowledgments

We thank Prof. Jun Yu from the Department of Mathematics and Mathematical Statistics at Umeå University for his support on statistical calculations.

Footnotes

  • Published online Jan. 22, 2015.

REFERENCES

  1. 1.↵
    1. Doot RK,
    2. Scheuermann JS,
    3. Christian PE,
    4. Karp JS,
    5. Kinahan PE
    . Instrumentation factors affecting variance and bias of quantifying tracer uptake with PET/CT. Med Phys. 2010;37:6035–6046.
    OpenUrlCrossRefPubMed
  2. 2.↵
    1. Kamasak ME
    . Computation of variance in compartment model parameter estimates from dynamic PET data. Med Phys. 2012;39:2638–2648.
    OpenUrlCrossRefPubMed
  3. 3.↵
    1. Li X,
    2. Feng D
    . Optimal design of scan intervals for glucose kinetic modeling using dynamic imaging data from PET. IEEE Eng Med Biol. 1994;1:634–5.
  4. 4.
    1. Cai W,
    2. Feng D,
    3. Fulton R
    . A fast algorithm for estimating FDG model parameters in dynamic PET with an optimised image sampling schedule and corrections for cerebral blood volume and partial volume. IEEE Eng Med Biol Soc. 1998;20:767–770.
    OpenUrl
  5. 5.
    1. D’Argenio DZ
    . Optimal sampling times for pharmacokinetic experiments. J Pharmacokinet Biopharm. 1981;9:739–756.
    OpenUrlCrossRefPubMed
  6. 6.↵
    1. Li X,
    2. Feng D,
    3. Chen K
    . Optimal image sampling schedule for both image-derived input and output functions in PET cardiac studies. IEEE Trans Med Imaging. 2000;19:233–242.
    OpenUrlCrossRefPubMed
  7. 7.↵
    1. Raylman RR,
    2. Caraher JM,
    3. Hutchins GD
    . Sampling requirements for dynamic cardiac PET studies using image-derived input functions. J Nucl Med. 1993;34:440–447.
    OpenUrlAbstract/FREE Full Text
  8. 8.↵
    1. Jovkar S,
    2. Evans AC,
    3. Diksic M,
    4. Nakai H,
    5. Yamamoto YL
    . Minimisation of parameter estimation errors in dynamic PET: choice of scanning schedules. Phys Med Biol. 1989;34:895–908.
    OpenUrlCrossRefPubMed
  9. 9.↵
    1. Barrett HH,
    2. Wilson DW,
    3. Tsui BMW
    . Noise properties of the EM algorithm: I. theory. Phys Med Biol. 1994;39:833–846.
    OpenUrlCrossRefPubMed
  10. 10.↵
    1. Razifar P,
    2. Sandström M,
    3. Schneider H,
    4. et al
    . Noise correlation in PET, CT, SPECT and PET/CT data evaluated using autocorrelation function: a phantom study on data, reconstructed using FBP and OSEM. BMC Med Imaging. 2005;5:5–23.
    OpenUrlCrossRefPubMed
  11. 11.↵
    1. Gulyás B,
    2. Halldin C
    . New PET radiopharmaceuticals beyond FDG for brain tumor imaging. Q J Nucl Med Mol Imaging. 2012;56:173–190.
    OpenUrlPubMed
  12. 12.↵
    1. Schiepers C,
    2. Dahlbom M,
    3. Chen W,
    4. et al
    . Kinetics of 3′-deoxy-3′-18F-fluorothymidine during treatment monitoring of recurrent high-grade glioma. J Nucl Med. 2010;51:720–727.
    OpenUrlAbstract/FREE Full Text
  13. 13.↵
    1. Schiepers C,
    2. Chen W,
    3. Dahlbom M,
    4. et al
    . 18F-fluorothymidine kinetics of malignant brain tumors. Eur J Nucl Med Mol Imaging. 2007;34:1003–1011.
    OpenUrlCrossRefPubMed
  14. 14.↵
    1. Spence AM,
    2. Muzi M,
    3. Link JM,
    4. et al
    . NCI-sponsored trial for the evaluation of safety and preliminary efficacy of 3′-deoxy-3′-[18F]fluorothymidine (FLT) as a marker of proliferation in patients with recurrent gliomas: preliminary efficacy studies. Mol Imaging Biol. 2009;11:343–355.
    OpenUrlCrossRefPubMed
  15. 15.↵
    1. Muzi M,
    2. Mankoff DA,
    3. Grierson JR,
    4. et al
    . Kinetic modeling of 3′-deoxy-3′-fluorothymidine in somatic tumors: mathematical studies. J Nucl Med. 2005;46:371–380.
    OpenUrlAbstract/FREE Full Text
  16. 16.↵
    1. Ikoma Y,
    2. Watabe H,
    3. Shidahara M,
    4. Naganawa M,
    5. Kimura Y
    . PET kinetic analysis: error consideration of quantitative analysis in dynamic studies. Ann Nucl Med. 2008;22:1–11.
    OpenUrlCrossRefPubMed
  17. 17.↵
    1. Lodge MA,
    2. Carson RE,
    3. Carrasquillo JA,
    4. et al
    . Parametric images of blood flow in oncology PET studies using [15O]water. J Nucl Med. 2000;41:1784–1792.
    OpenUrlAbstract/FREE Full Text
  18. 18.↵
    1. Jan S,
    2. Santin G,
    3. Strul D,
    4. et al
    . GATE: a simulation toolkit for PET and SPECT. Phys Med Biol. 2004;49:4543–4561.
    OpenUrlCrossRefPubMed
  19. 19.↵
    1. Schmidtlein CR,
    2. Kirov AS,
    3. Nehmeh SA,
    4. et al
    . Validation of GATE Monte Carlo simulations of the GE Advance/Discovery LS PET scanners. Med Phys. 2006;33:198–208.
    OpenUrlCrossRefPubMed
  20. 20.↵
    1. Collins DL,
    2. Zijdenbos AP,
    3. Kollokian V,
    4. et al
    . Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998;17:463–468.
    OpenUrlCrossRefPubMed
  21. 21.↵
    1. Häggström I,
    2. Schmidtlein CR,
    3. Karlsson M,
    4. Larsson A
    . Compartment modeling of dynamic brain PET: the impact of scatter corrections on parameter errors. Med Phys. 2014;41:111907–111909.
    OpenUrlCrossRefPubMed
  22. 22.↵
    1. Contractor KB,
    2. Kenny LM,
    3. Coombes CR,
    4. et al
    . Evaluation of limited blood sampling population input approaches for kinetic quantification of [18F]fluorothymidine PET data. Eur J Nucl Med Mol Imaging. 2012;2:1–11.
  23. 23.↵
    1. Mitev K,
    2. Gerganov G,
    3. Kirov AS,
    4. et al
    . Influence of photon energy cuts on PET Monte Carlo simulation results. Med Phys. 2012;39:4175–4186.
    OpenUrlCrossRefPubMed
  24. 24.↵
    1. Kinahan PE,
    2. Rogers JG
    . Analytic 3D image reconstruction using all detected events. IEEE Trans Nucl Sci. 1989;36:964–968.
    OpenUrlCrossRef
  25. 25.↵
    1. Hudson HM,
    2. Larkin RS
    . Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans Med Imaging. 1994;13:601–609.
    OpenUrlCrossRefPubMed
  26. 26.↵
    1. Thielemans K,
    2. Tsoumpas C,
    3. Mustafovic S,
    4. et al
    . STIR: software for tomographic image reconstruction release 2. Phys Med Biol. 2012;57:867–883.
    OpenUrlCrossRefPubMed
  27. 27.↵
    1. Schmidtlein CR,
    2. Turner A,
    3. Nehmeh SA,
    4. et al
    . SU-FF-I-54: A Monte Carlo model of the Discovery ST PET scanner [abstract]. Med Phys. 2006;33:2009.
    OpenUrl
  28. 28.↵
    1. Thielemans K,
    2. Sauge D,
    3. Labbé C,
    4. et al
    . Software for Tomographic Image Reconstruction User’s Guide: Version 3.0. Source Forge website. http://stir.sourceforge.net/documentation/STIR-UsersGuide.pdf. Accessed February 5, 2015.
  29. 29.↵
    1. Tsoumpas C,
    2. Aguiar P,
    3. Nikita KS,
    4. Ros D,
    5. Thielemans K
    . Evaluation of the single scatter simulation algorithm implemented in the STIR library. IEEE Nucl Sci Symp Conf Rec. 2004;6:3361–3365.
  30. 30.↵
    1. Yaqub M,
    2. Boellaard R,
    3. Kropholler MA,
    4. Lammertsma AA
    . Optimization algorithms and weighting factors for analysis of dynamic PET studies. Phys Med Biol. 2006;51:4217–4232.
    OpenUrlCrossRefPubMed
  31. 31.↵
    1. Thiele F,
    2. Buchert R
    . Evaluation of non-uniform weighting in non-linear regression for pharmacokinetic neuroreceptor modelling. Nucl Med Commun. 2008;29:179–188.
    OpenUrlCrossRefPubMed
  32. 32.↵
    1. Reilhac A,
    2. Tomeï S,
    3. Buvat I,
    4. et al
    . Simulation-based evaluation of OSEM iterative reconstruction methods in dynamic brain PET studies. Neuroimage. 2008;39:359–368.
    OpenUrlCrossRefPubMed
  33. 33.↵
    1. Walker MD,
    2. Julyan PJ,
    3. Talbot PS,
    4. Jones T,
    5. Matthews JC
    . Bias in iterative reconstruction of low-statistics PET data: benefits of a resolution model. IEEE Nucl Sci Symp Conf Rec. 2009;2857–2863.
  34. 34.↵
    1. Boellaard R,
    2. van Lingen A,
    3. Lammertsma AA
    . Experimental and clinical evaluation of iterative reconstruction (OSEM) in dynamic PET: quantitative characteristics and effects on kinetic modeling. J Nucl Med. 2001;42:808–817.
    OpenUrlAbstract/FREE Full Text
  35. 35.↵
    1. de Geus-Oei LF,
    2. Visser EP,
    3. Krabbe PFM,
    4. et al
    . Comparison of image-derived and arterial input functions for estimating the rate of glucose metabolism in therapy-monitoring 18F-FDG PET studies. J Nucl Med. 2006;47:945–949.
    OpenUrlAbstract/FREE Full Text
  • Received for publication April 15, 2014.
  • Accepted for publication November 19, 2014.
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Keywords