Abstract
The aim of this study was to optimize the number of iterations in bone SPECT imaging using a novel thoracic spine phantom (ISMM phantom). Methods: The quality and quantitative accuracy of bone SPECT images were evaluated by changing the number of iterations and the size of the hot spot in the phantom. True SUVs in the vertebra, tumor, and background parts were 9.8, 52.2, and 1.0, respectively. The phantom image was reconstructed using the ordered-subset expectation-maximization algorithm with CT-based attenuation correction, scatter correction, and resolution recovery; the number of ordered-subset expectation-maximization subsets was fixed at 10, with iterations ranging from 1 to 40. Full width at half maximum, percentage coefficient of variation, contrast ratio for the sphere and background (contrast), and recovery coefficient were evaluated as a function of the number of iterations for a given number of subsets (10) using the reconstructed images. In addition, SUVmax, SUVpeak, and SUVmean were calculated with various numbers of iterations for each sphere (13, 17, 22, and 28 mm) simulating a tumor. Results: Full width at half maximum decreased as the number of iterations was increased, and full width at half maximum converged uniformly when the number of iterations exceeded 10. The percentage coefficient of variation increased as the number of iterations was increased. Recovery coefficient decreased with decreasing sphere size. Contrast and all SUVs increased as the number of iterations was increased, and contrast and all SUVs converged uniformly when the number of iterations exceeded 5 and 10, respectively, for all sphere sizes. When the SUV was defined as the converged value for 10 iterations in the 28-mm sphere, the converged values of SUVmax, SUVpeak, and SUVmean were 75.1, 66.5, and 55.6, respectively. The relative error in the converged values for SUVmax, SUVpeak, and SUVmean were 43.8%, 27.3%, and 7.2% of the true value (52.2); all SUVs were overestimated. Conclusion: Using a thoracic spine phantom to evaluate the optimal reconstruction parameters in bone SPECT imaging, we determined the optimal number of iterations for 10 subsets to be 10.
Quantitative analysis using SUVs from PET has been performed in the clinical setting to decide treatment strategies and predict recurrence after treatment (1,2). With the recent development of attenuation correction, scatter correction, and resolution recovery, quantitative analysis has also been performed in SPECT in nuclear medicine imaging (3). In particular, SUVs calculated from bone SPECT imaging can be used to make more accurate diagnoses (4–6).
SUVs are quantitative measures of normalized radioactivity concentration in reconstructed images. Calculating the SUV requires the reconstructed SPECT count within the volume of interest (VOI), injected activity, patient body size, and a cross-calibration factor. Therefore, for quantitative accuracy, it is necessary to obtain an accurate SPECT count from reconstructed images. However, the measured SPECT counts are strongly affected by reconstruction parameters, especially the number of iterations and subsets (7). SPECT image quality is also affected by the number of iterations and subsets. Therefore, the optimal number of iterations for bone SPECT imaging should be determined to improve quantitative accuracy and image quality.
A commercially available phantom (National Electrical Manufacturers Association/International Electrotechnical Commission body phantom; Data Spectrum) has been used in several previous studies (8–10). Using this phantom, Myint et al. reported that SUVs were affected by the number of iterations (9). The body phantom was developed to optimize the acquisition of tumors and related reconstruction parameters in PET imaging (11). Although the body phantom is simple and easy to use, the structure of the trunk and bone is not simulated. Thus, a novel thoracic spine phantom (ISMM phantom; Kyoto Kagaku Co., Ltd.) has been developed that comprises a trunk, a vertebral body, tumors, and transverse and spinous processes and contains a K2HPO4 solution with a density equivalent to that of bone, thereby more accurately reproducing parameters to use for optimization.
The aim of this study was to use the ISMM thoracic spine phantom to optimize iteration and subset reconstruction parameters in bone SPECT imaging. The quality and quantification accuracy of bone SPECT images were evaluated by changing the number of iterations and the size of the hot spot when the number of subsets was fixed at 10 in the phantom. Then, we determined the most appropriate number of iterations with 10 subsets for bone SPECT reconstruction using attenuation correction, scatter correction, and resolution recovery.
MATERIALS AND METHODS
ISMM Phantom
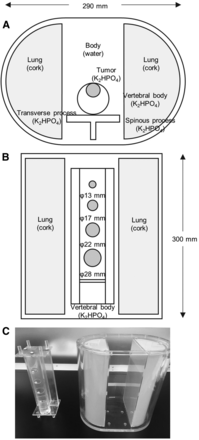
Photos and diagrams of the ISMM phantom are shown in Figure 1. The phantom simulates part of the spine, making it possible to evaluate the specific radioactivity distribution and linear photon attenuation coefficient in bone SPECT imaging. The phantom consists of 4 parts: a trunk (background), a cylinder (vertebra), 4 spheres of different sizes (tumors), and a T-shaped container (transverse and spinous processes). The axis and height of the trunk were 290 and 300 mm, respectively. The diameters of the spheres simulating tumors were 13, 17, 22, and 28 mm. The vertebra and tumor parts were respectively filled with 63.6 and 339.0 kBq/mL of 99mTc in a K2HPO4 bone-equivalent solution. K2HPO4 is known to have a photon coefficient similar to that of bone. The concentration of the K2HPO4 solution was suggested by de Dreuille et al. (12). The K2HPO4 solution was made by dissolving 100 g of K2HPO4 in 67 g of distilled water. The background part was filled with a 6.5 kBq/mL solution of 99mTc. The radioactive concentrations in the vertebra and tumor parts were based on the radioactive concentrations of healthy vertebral cancellous bone and the SUV of bone metastases (13,14). The true SUVs of the vertebra, tumors, and background parts were 9.8, 52.2, and 1.0, respectively.
(A) Axial diagram of ISMM phantom. (B) Coronal diagram of ISMM phantom. (C) Photograph of thoracic spine ISMM phantom; vertebra and tumors are shown on left, and torso and lungs are shown on right.
SPECT/CT Scanner and Acquisition
All SPECT data were acquired with a dual-head SPECT/CT camera (Infinia8 Hawkeye 4; GE Healthcare) with a low-energy, high-resolution collimator. The camera was equipped with a 2.54-cm (1-in)-thick detector crystal having a lattice slit and 95 photomultiplier tubes, giving it a sensitivity approximately 8% higher than that of a camera equipped with a 0.9525-cm (3/8-in) detector crystal (15). The CT component was a low-dose multislice CT system. The SPECT projection data were obtained in continuous mode, 1 min/rotation for 15 repetitions with a 128 × 128 matrix and a viewing angle of 3°. The energy windows and the scatter window were set at 140.0 keV ± 10% and 120.0 keV ± 5%, respectively. The distance from collimator to phantom was set to 230 mm. The CT scan parameters were as follows: slice thickness, 6.1 mm; slice spacing, 4.42 mm; matrix, 512 × 512; voltage, 140 kV; current, 2.5 mA; helical pitch, 1.9.
Image Reconstruction
The phantom image was reconstructed using the ordered-subset expectation-maximization algorithm with CT-based attenuation correction, scatter correction, and resolution recovery, using the software Evolution (GE Healthcare). The number of ordered-subset expectation-maximization subsets was fixed at 10, and the number of iterations was varied from 1 to 40. A Butterworth filter (order, 10; cutoff frequency, 0.40 cycles/cm) was used for postprocessing.
Data Analysis
Full width at half maximum (FWHM), percentage coefficient of variation (%CV), sphere-to-background contrast ratio (contrast), and recovery coefficient (RC) were evaluated as a function of the spatial resolution, uniformity, detectability, and quantitative accuracy, respectively. Linear profiles were plotted on the spinous process in the reconstructed images, and the FWHM was calculated. A background region of interest with an area of 13 mm3 was placed on the trunk of the phantom. The %CV, contrast, and RC were calculated as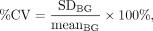


where meansphere is the mean counts per pixel in each sphere region of interest, meanBG is the mean counts per pixel in the background region of interest, and SDBG is the SD of the counts per pixel in the background region of interest. A and a are the true activity concentration and the measured activity concentration, respectively, for each sphere. The linear profiles and the region of interest were set in 5 slices, and each calculated value was averaged.
SUVmax, SUVpeak, and SUVmean were calculated as
where C is the SPECT count within a VOI (cps), CCF is a cross-calibration factor (Bq/cps), a BG is the background radioactivity (Bq), and w is the background weight of the phantom (g). VOI was defined for the tumor, vertebra, and background parts using the software GI-BONE (AZE Co., Ltd.) (Fig. 2) . For each number of iterations, the cross-calibration factor was obtained automatically from the relationship between radioactivity and counts per second of a cylinder phantom using GI-BONE. The diameter of the VOI in the tumor part was set to 90% of the size of each sphere; the vertebra part was used as a reference. The radioactivity concentration was measured within the VOIs. The maximum and average radioactivity concentrations were used for SUVmax and SUVmean, respectively. SUVpeak was defined as the average SUV in a 10-mm sphere for the highest uptake region within the VOI. The relative error was found in the measured SUV compared with the true SUV. Reconstructed images with various numbers of iterations were compared visually in sagittal images. Bone SPECT image quality was visually assessed by 10 radiology technologists and 10 specialists in nuclear medicine from different hospitals. The degree of quality for bone SPECT was classified into 4 grades: 1 (poor), not suitable; 2 (average), neutral; 3 (good), suitable; and 4 (excellent), most suitable. The average score was calculated for each number of iterations, and statistical analysis was performed using the Friedman test, with a P value of less than 0.05 considered statistically significant.
Axial (A) and coronal (B) diagrams of VOIs. VOIs 1, 2, and 3 were defined as background, tumor (28 mm), and vertebra, respectively. VOIs of other tumor sizes were defined similarly to 28-mm tumor.
RESULTS
FWHM, %CV, Contrast, and RC
The FWHM, %CV, and contrast plotted versus the number of iterations and the RC plotted versus the size of the sphere are shown in Figures 3 and 4, respectively. The FWHM decreased as the number of iterations was increased, and FWHM converged uniformly when the number of iterations exceeded 10. Defined as when the number of iterations was 10, the converged FWHM value was 18.4 mm. The %CV increased as the number of iterations was increased. Contrast increased as the number of iterations was increased, and contrast converged uniformly when the number iterations exceeded 5. Defined as when the number of iterations exceeded 5, the converged contrast was 46.8, 19.4, 9.6, and 6.6 for spheres with diameters of 28, 22, 17, and 13 mm, respectively. The RC decreased when the diameters and the number of iterations decreased. The RC was approximately 1.00 for the sphere with a diameter of 28 mm when the number of iterations was from 2–40, but the RC was underestimated by 54% or more for spheres with diameters of 22, 17, and 13 mm.
Comparison of FWHM (A), %CV (B), and contrast (C) according to number of iterations. Number of subsets was fixed at 10, and number of iterations was varied from 1 to 40. FWHM decreased as number of iterations was increased, and FWHM converged uniformly when number of iterations exceeded 10. %CV increased as number of iterations was increased. Contrast increased as number of iterations was increased, and contrast converged uniformly when number of iterations exceeded 5.
Comparison of RC by size of sphere. Number of subsets was fixed at 10, and number of iterations was varied from 1 to 40. RC decreased with decreasing sphere size.
SUV
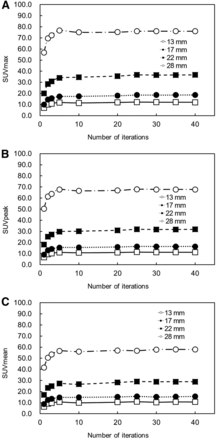
For each sphere, SUVmax, SUVpeak, and SUVmean plotted versus the number of iterations are shown in Figure 5. All SUVs increased as the number of iterations was increased, and all SUVs converged uniformly when the number of iterations exceeded 10 in spheres of all sizes. The converged value increased as the size of the spheres increased and was largest for the 28-mm sphere. The SUVmean when the number of iterations was 10 was 55.9, 27.2, 14.7, and 9.9 for spheres with diameters of 28, 22, 17, and 13 mm, respectively. The SUVmean of the 28-mm sphere was approximately 5 times that of the 13-mm sphere. Defined as when the number of iterations was 10 in the 28-mm sphere, the converged values of SUVmax, SUVpeak, and SUVmean were 75.1, 66.5, and 55.6, respectively. The relative error in the converged values of SUVmax, SUVpeak, and SUVmean were 43.8%, 27.3%, and 7.2% of the true value, respectively (52.2). All SUVs were overestimated.
Comparison of SUVmax (A), SUVpeak (B), and SUVmean (C) according to number of iterations. Number of subsets was fixed at 10, and number of iterations was varied from 1 to 40. As number of iterations was increased, all SUVs increased and converged uniformly.
Visual Assessment
SPECT images and the results of visual assessment for varying numbers of iterations are shown in Figure 6 and Table 1, respectively. The average assessment score tended to be higher with 10 iterations or more than with fewer than 10 iterations. The highest average score was obtained with 10 and 35 iterations. However, there was no significant difference according to the number of iterations. There was a significant difference between the observers.
SPECT images of thoracic spine with various numbers of iterations. Number of subsets was fixed at 10, and number of iterations was 1, 2, 3, 5, 10, 20, 25, 30, 35, and 40.
Visual Assessment Results Varied According to Numbers of Iterations
DISCUSSION
In this study, the quality and quantitative accuracy of bone SPECT images were evaluated by changing the number of iterations and the size of the hot spot in the phantom to optimize the reconstruction parameters using a novel thoracic spine phantom. The results showed that the number of iterations influenced spatial resolution, image uniformity, and detectability. Furthermore, all SUVs for all sphere sizes increased as the number of iterations was increased, and all SUVs converged uniformly when the number of iterations was 10. Using the optimal parameter, the relative error between the measurement value at 10 iterations and the true value was 43.8% for SUVmax, 27.3% for SUVpeak, and 7.2% for SUVmean in the 28-mm sphere.
A novel thoracic spine phantom called the ISMM phantom was used in this study. A K2HPO4 bone-equivalent solution was used in the phantom to realize more accurate bone assessment. Iida et al. used the same solution in a 3-dimensional brain phantom and found attenuation μ-values similar to results obtained in real people (16). An accurate attenuation correction map might not be generated without the use of bone-equivalent solution. Therefore, using the phantom enables accurate attenuation correction to be performed and appropriate reconstruction parameters to be determined.
The FWHM decreased as the number of iterations was increased, and the FWHM converged uniformly when the number of iterations was 10. The %CV increased as the number of iterations was increased. The contrast increased as the number of iterations was increased, and the contrast converged uniformly when the number iterations exceeded 5. Miyaji et al. reported that the FWHM at the spinous process was 15 mm using xSPECT Quant (17). Although these results are nearly identical to the present results, the FWHM in our study was slightly larger because of the thickness of the detector crystals. The uniformity decreased as the number of iterations was increased because the statistical noise increased as well. Sakai et al. reported that %CV increased as the number of iterations was increased using ordered-subset expectation maximization. The method statistically estimates the source distribution, thus emphasizing the statistical noise in the image (18). Contrast is one of the most important parameters to evaluate because detection of hot spots is used for diagnosis in bone SPECT (19). However, there was a trade-off between FWHM, contrast, and %CV; therefore, these values should be balanced to determine the optimal reconstruction parameters.
In the visual assessment, images with 10 iterations or more that had a high contrast also had a high score. Detectability rather than uniformity was emphasized in the bone SPECT (19). However, there was no significant difference between the numbers of iterations according to visual assessment. In contrast, there was a significant difference between the observers. Peters et al. reported the importance of harmonizing differences in absolute quantitative SPECT among multiple facilities because the influence of several reconstruction parameters was decreased by harmonization (10). In this study, an ISMM phantom image was visually assessed by observers from different hospitals. However, there were significant differences in the results among these observers. It is possible that the best quality for the bone SPECT image differed according to the hospital. Therefore, further study is required to harmonize the criteria for image quality among facilities.
All SUVs increased as the number of iterations was increased, and all SUVs converged uniformly when the number of iterations was 10 for all sphere sizes. Therefore, the optimal number of iterations was determined to be 10, considering the FWHM and %CV. Matsutomo et al. reported that the optimal subset × iteration (update number) was 90 in a dopamine transporter SPECT study (20). In addition, Dickson et al. reported that an ordered-subset expectation maximization using an update number of 100 provided good image quality and quantification accuracy (21). Although our results are not directly comparable to those reports because of the different phantoms and reconstruction algorithms used, the determined update number was considered appropriate for bone SPECT imaging. Recently, the clinical utility of the quantitative approach using SUVs has been reported in bone SPECT imaging (4–6). However, various parameters were used for reconstruction in each study. Suh et al. evaluated the efficiency of the SUV for temporomandibular joint disorder using 2 iterations and 10 subsets (22), and Beck et al. evaluated the efficiency of the SUV for bone metabolism using 8 iterations and 4 subsets (23). Had the optimized reconstruction parameters been used to calculate the SUV, different results might have been obtained in these earlier studies. Therefore, standardized reconstruction parameters determined using anthropomorphic phantoms composed of clinical structures, including the Hoffman 3D Brain Phantom (Data Spectrum Corp.) and myocardial phantom, are needed for quantitative SPECT imaging.
The SUVs of spheres with diameters of 13, 17, and 22 mm were found to be less than the true values, and RC decreased with decreasing sphere size. These results were caused by a partial-volume effect that occurred whenever the sphere size was less than 3 times the FWHM (24). Furthermore, a partial-volume effect might occur even when the sphere size is more than 3 times the spatial resolution (25). Quantitative accuracy is expected to be improved by applying the partial-volume-effect correction method (26); however, this was beyond the scope of the present study. For the 28-mm sphere, SUVmax and SUVpeak were clearly higher than the true values. There are 2 reasons for these results. First, the measurement accuracy of SUV is affected by image noise (8). Second, we used a resolution-recovery algorithm in this study. Onishi et al. reported that the count variation at a diameter of 16–28.8 mm was caused by Gibbs oscillation when using resolution recovery (27). An edge artifact was not observed visually for the ISMM phantom image in this study. However, there is the possibility that the Gibbs oscillation occurred as a result of using the resolution-recovery algorithm. Image noise and Gibbs oscillation might have been present in our results, and thus attention is needed to interpret the quantitative parameters.
There were some limitations to this study. First, although the SUV was influenced by the reconstruction parameters and reconstruction algorithm, only one reconstruction algorithm (Evolution) was used for this evaluation. Nakahara et al. reported that the SUV was influenced by differences among several SPECT/CT systems (8). Therefore, the reconstruction parameters when using another algorithm should be determined in a future study. Second, the reconstruction parameters were determined using only the phantom because this was a basic study. Accordingly, the effect of reconstruction parameters should be investigated in clinical patients in future studies. Third, the phantom did not mimic soft tissue. Therefore, the quantitative accuracy might have been affected by the difference in photon attenuation coefficient between water and soft tissue.
CONCLUSION
The optimal number of iterations was evaluated as a reconstruction parameter in bone SPECT imaging using a thoracic spine phantom. The SUV was influenced by the reconstruction parameters. The optimal number of iterations for the 10 subsets was determined to be approximately 10 considering image quality and quantitative accuracy.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Footnotes
Published online Dec. 24, 2020.
REFERENCES
- Received for publication July 13, 2020.
- Accepted for publication December 10, 2020.