Abstract
A dedicated stationary cardiac single-photon emission computed tomography (SPECT) system with a novel segmented slant-hole collimator has been developed. The goal of this paper is to calibrate this new imaging geometry with a point source. Methods: Unlike the commercially available dedicated cardiac SPECT systems, which are specialized and can be used only to image the heart, our proposed cardiac system is based on a conventional SPECT system but with a segmented slant-hole collimator replacing the collimator. For a dual-head SPECT system, 2 segmented collimators, each with 7 sections, are arranged in an L-shaped configuration such that they can produce a complete cardiac SPECT image with only one gantry position. A calibration method was developed to estimate the geometric parameters of each collimator section as well as the detector rotation radius, under the assumption that the point source location is calculated using the central-section data. With a point source located off the rotation axis, geometric parameters for each collimator section can be estimated independently. The parameters estimated individually are further improved by a joint objective function that uses all collimator sections simultaneously and incorporates the collimator symmetry information. Results: Estimation results and images reconstructed from estimated parameters are presented for both simulated and real data acquired from a prototype collimator. The calibration accuracy was validated by computer simulations with an error of about 0.1° for the slant angles and about 1 mm for the rotation radius. Reconstructions of a heart-insert phantom did not show any image artifacts of inaccurate geometric parameters. Conclusion: Compared with the detector’s intrinsic resolution, the estimation error is small and can be ignored. Therefore, the accuracy of the calibration is sufficient for cardiac SPECT imaging.
Dedicated cardiac SPECT systems based on state-of-the-art detector technologies and specific acquisition geometries offer ultrafast scans with high image quality for the detection of coronary artery disease. Very short acquisition times can be achieved mainly through the use of multidetectors or multicollimators (e.g., pinhole or slant hole) that are oriented from different directions and image the heart simultaneously (1–5). Adding detectors also adds more parameters to be calibrated. As compared with the conventional parallel-hole system, the cardiac SPECT system with sophisticated collimators is more difficult to calibrate. Knowledge of the precise geometric parameters is essential for accurate image reconstruction.
The optimal method for calibration depends on the scanner geometry. Many geometric calibration methods have been proposed since the early 1980s (6–10). For parallel and slant geometry, Busemann-Sokole presented a calibration procedure that entailed measuring a plate containing 16 point sources at 2 different positions (6). For fanbeam geometry, a method of minimizing the distance between the experimental measurement and the analytic locations of one point source was proposed by Gullberg et al. (7) and was extended to cone beam geometry (8). A good approximation of initial values was required to avoid unrealistic solutions. More recently, multiple point sources with known relative distances were applied in calibration to eliminate correlation of scanner parameters (9–12). Although this method needs only coarse initial values, the design of the calibration object requires high precision.
The aim of this paper is to develop a geometric calibration procedure for a prototype dedicated stationary cardiac SPECT system with segmented slant-hole collimators. This stationary cardiac SPECT system is realized by simply mounting the segmented slant-hole collimators on the widely used 2-head conventional SPECT system. Each collimator includes 7 subcollimators slanted toward a common volume at the rotation center. With 2 γ-camera detectors 90° apart, 14 views are acquired simultaneously. To obtain a high-quality reconstruction, precise calibration of geometric parameters is necessary.
Even though our system is able to produce a cardiac image without gantry rotation, we rotate the gantry 180° for the system calibration procedure. Our method consists of 2 steps. In the first, the central subsection that has the conventional parallel-hole collimator is used to estimate the location of the point source. When the location of the point source is measured, the parameter estimation problem becomes a minimization problem with a quadratic objective function. The quadratic nature of the objective function enables closed-form estimation. Parameters for each section are estimated independently. In the second, a joint objective function can be set up in the second step, so that all parameters can be estimated simultaneously. The joint objective function can incorporate the collimator symmetry information and makes the estimation more accurate.
This paper is organized as follows. In the first section, we briefly introduce the segmented slant-hole stationary cardiac SPECT system and explain the details of the proposed calibration method. Our method has been verified by Monte Carlo simulations and actual system measurements. In Monte Carlo simulations, the ground truth is known. In real data studies, the projections were acquired with a prototype system with a segmented slant-hole collimator, and then the geometric parameters were estimated. The validation and calibration results are illustrated in the second section. Finally, we discuss the results and summarize the paper.
MATERIALS AND METHODS
Segmented Slant-Hole Collimator
The proposed slant-hole collimator has 7 segments, as shown in Figure 1. Section I is the conventional parallel-hole collimator. Sections II–VII are slant-hole collimators. Within a section, the collimator holes are parallel to each other. The region in front of the collimators, which is “seen” by all sections, is the common volume centered at the rotation center (Fig. 2). The region of interest must be contained in the common volume.
Illustration of proposed 7-segment slant-hole collimator. Projection is elongated at outer sections. Dashed ellipses represent projection on that section of detector when sphere is placed at rotation center.
Cross section of common volume (CV) in x,y-plane.
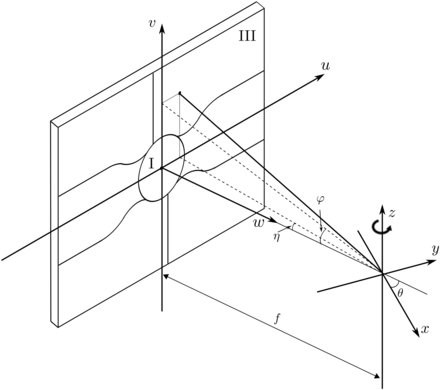
Without loss of generality, we use section III to introduce slant angles as shown in Figure 3. The slant angles of each section must be estimated before image reconstruction can be performed. To describe the geometry of the scanner, we introduce 2 sets of axes: the detector and the object axes. The detector axes is defined by (u, v, w), where the u-axis refers to the horizontal axis, the v-axis refers to the vertical axis that is parallel to the rotation axis of the detector, and the w-axis is normal to the detector and oriented toward the rotation axis.
Definition of slant angles η and φ, detector coordinates, and object coordinates. z-axis is rotation axis of detector.
The object is defined in the (x, y, z) system. In this paper, we define the origin of the object system to be at the intersection of the w-axis and the rotation axis, and the rotation axis is referred to as the z-axis. When the detector rotation angle is θ = 0°, the u-axis is parallel to the y-axis.
The transformation from the (x, y, z) coordinate system to the (u, v, w) coordinate system is equivalent to a clockwise rotation about the z-axis by angle θ plus a shift of rotation radius f in the w direction. The final transformation is given by
 Eq. 1
Eq. 1
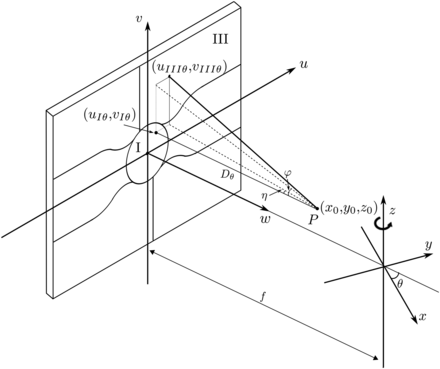
This paper proposes a method to estimate the slant angles η and φ for each section. The definitions of slant angles η and φ are illustrated in Figure 3. The detector rotation radius f will also be estimated. This method uses one point source P at the location (x
0, y
0, z
0) that is away from the rotation axis. Without loss of generality, again, we use section III to show the setup of the point source P relative to the detector, as shown in Figure 4. The location of P can be obtained using 2 or more views from a conventional parallel-hole collimator—for example, section I of our proposed segmented collimator. According to Figure 4, the image of point source P in section I has the coordinates
 Eq. 2
and the distance from the point source P to the detector is
Eq. 2
and the distance from the point source P to the detector is
 Eq. 3
The image of the point source P in section III is related to (
Eq. 3
The image of the point source P in section III is related to (
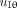 ,
,
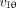 ) as, according to Figure 4,
) as, according to Figure 4,
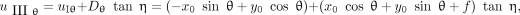 Eq. 4
Eq. 4
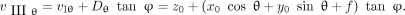 Eq. 5
Eq. 5
Setup of point source P.
In our system, the distance from the rotation axis to the back of the collimator is referred to as the rotation radius of the collimator (Figs. 3 and 4). Because the dual-detector E-CAM Signature Series SPECT system (Siemens Healthcare) on which the segmented slant-hole collimator is mounted is already calibrated, the mechanical shifts in the u- and v-directions are not calibrated in this procedure. Calibration is performed once, after the collimator is fabricated, and is not required for each patient. Here, we define the center of the detector to be the origin of the (u, v) coordinate system, which is also the center of section I. The center coordinates of other outer sections are defined as (f tan η, f tan φ) as shown in Figure 3.
Calibration of Segmented Slant-Hole Collimator
Independent Estimation of the Parameters
In Equations 4 and 5, the measurements are
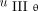 and
and
 . The point source location is also assumed to be known, because it can be estimated by using the projection data from section I. (Appendix A presents the method we used to obtain the parameters.) Thus, the unknowns to be estimated are tan η, tan φ, and f.
. The point source location is also assumed to be known, because it can be estimated by using the projection data from section I. (Appendix A presents the method we used to obtain the parameters.) Thus, the unknowns to be estimated are tan η, tan φ, and f.
On the basis of Equations 4 and 5, the unknowns can be estimated by minimizing the following error functions:
 Eq. 6
Eq. 6
 Eq. 7
These error functions are the usual quadratic objective functions. This becomes obvious if Equation 6 is rewritten as
Eq. 7
These error functions are the usual quadratic objective functions. This becomes obvious if Equation 6 is rewritten as
 Eq. 8
with the unknown variables defined as
Eq. 8
with the unknown variables defined as
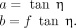 Eq. 9
Taking partial derivatives of E
u with respect to a and b, respectively, and setting the partial derivatives to zero, we have
Eq. 9
Taking partial derivatives of E
u with respect to a and b, respectively, and setting the partial derivatives to zero, we have
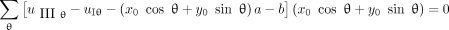 Eq. 10
Eq. 10
 Eq. 11
that is,
Eq. 11
that is,
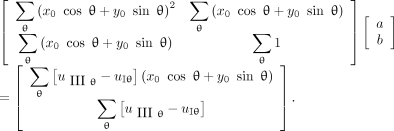 Eq. 12
Therefore, the closed-form solutions for a and b are obtained as
Eq. 12
Therefore, the closed-form solutions for a and b are obtained as
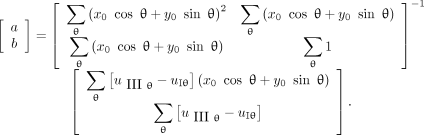 Eq. 13
Note that when x
0 ≠ 0 and y
0 ≠ 0, the solution is unique.
Eq. 13
Note that when x
0 ≠ 0 and y
0 ≠ 0, the solution is unique.
The geometric parameters η and f can be obtained as
 Eq. 14
Eq. 14
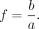 Eq. 15
Similarly, the solution for tan φ can be obtained by minimizing the objective function 7.
Eq. 15
Similarly, the solution for tan φ can be obtained by minimizing the objective function 7.
Joint Estimation of the Parameters
Notice that parameter f is estimated from both Equation 6 and Equation 7, and for all outer collimator sections. The outliers can be discarded, and the average value of these f values can be used. In fact, to further improve the accuracy of the parameters, a joint objective function using all collimator sections can be set up in Equation 18 below. Some extra information can be added to this new joint objective function. For example, the collimator is symmetric. Sections II and VII are mirror symmetric. Sections III and VI are mirror symmetric. Sections IV and V are mirror symmetric. This joint objective function can be further simplified if the point source P can be carefully positioned on the axis of rotation. The mirror symmetry property is able to average and reduce the errors generated in the individual estimation method discussed as in the previous section. Let us consider two special cases.
In the first special case (using 2 orthogonal views), we set 2 detectors at 0° and 90°, respectively, to acquire 2 high-count (i.e., low-noise) projection data of a point source. The location of the point source is given in section I, as x
0 =
 , y
0 =
, y
0 =
 , z
0 =
, z
0 =
 . Thus, (x
0, y
0, z
0) is known. Using 2 projections at 0° and 90°, expressions of f tan η and tan φ can be derived from Equations 4 and 5. Take section III as an example:
. Thus, (x
0, y
0, z
0) is known. Using 2 projections at 0° and 90°, expressions of f tan η and tan φ can be derived from Equations 4 and 5. Take section III as an example:
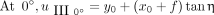 Eq. 16a
Eq. 16a
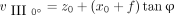 Eq. 17a
Eq. 17a
 Eq. 16b
Eq. 16b
 Eq. 17b
Combining Equations 16a and 16b yields Equation 16 below, and combining Equations 17a and 17b yields Equation 17 below:
Eq. 17b
Combining Equations 16a and 16b yields Equation 16 below, and combining Equations 17a and 17b yields Equation 17 below:
 Eq. 16
Eq. 16
 Eq. 17
Eq. 17
A joint objective function is then readily formed by Equations 16 and 17 by considering all outer sections simultaneously,
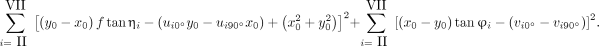 Eq. 18
Here, x
0 ≠ y
0. The collimator is symmetric with respect to the center; we enforce that ηII = −ηVII, ηIII
= −ηIV, ηIV = −ηV. All the unknown parameters—f, ηi, and φι—are iteratively updated to minimize the objective function 18, and the parameters vary in only a small range. Values for the independent-estimation step are used as the initial values.
Eq. 18
Here, x
0 ≠ y
0. The collimator is symmetric with respect to the center; we enforce that ηII = −ηVII, ηIII
= −ηIV, ηIV = −ηV. All the unknown parameters—f, ηi, and φι—are iteratively updated to minimize the objective function 18, and the parameters vary in only a small range. Values for the independent-estimation step are used as the initial values.
In the second special case (using one view with the point source on the axis of rotation), if we are able to carefully position the point source on the rotation axis by using the detector L-shaped configuration, the above formulation can be further simplified: x
0 = y
0 = 0. When the point source is placed on the rotation axis, the sinogram will be a straight line. We thus can use only one view to estimate the slant angles. When x
0 = y
0 = 0, Equations 4 and 5 are independent of rotation angle θ and are reduced to
 Eq. 19
Eq. 19
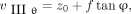 Eq. 20
which depend only on the parameters of the slant-hole geometry. The joint objective function for ηi and φi can readily be set up by Equations 4 and 5 as
Eq. 20
which depend only on the parameters of the slant-hole geometry. The joint objective function for ηi and φi can readily be set up by Equations 4 and 5 as
 Eq. 21
where (u
i, v
i) is the projection location of the point source at the
Eq. 21
where (u
i, v
i) is the projection location of the point source at the
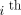 outer collimator section.
outer collimator section.
To summarize the estimation procedure, we first use a point source dataset with the point source off the axis of rotation and 2 projections at 0° and 90° in section I to obtain the point source location (x 0, y 0, z 0). Second, independent estimation of f, ηi, and φι is obtained. Finally, the estimates of f, ηi, and φι are used as the initial values and further refined using an iterative method to minimize the objective function 18 (Appendix A). If the point source happens to be placed on the rotation axis, Equation 21 is applied.
Geometric Point Response Function for Slant-Hole Collimator
To reduce the dead zone of the slant collimators, the collimator hole-length is chosen to be very short, resulting in a low-energy high-sensitivity collimator. Thus, geometric-blurring compensation is necessary. The differences between the point response functions for the conventional parallel-hole system and the slant-hole system are shown in Figure 5. The point response function is symmetric for the conventional parallel-hole collimator. However, for the slant-hole collimator, the point response function is asymmetric (13). The point response function is elongated in the direction of angle β as shown in Figure 6. The tilt angle α and the slant angle β are calculated as
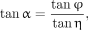 Eq. 22
Eq. 22
 Eq. 23
Eq. 23
Illustration of geometric response for parallel holes and slant holes.
Close-up diagram of footprint of point response function with respect to slant angles α and β.
Experiments
Experiments were performed using simulated and real data acquired from a prototype segmented slant-hole SPECT system. The maximum-likelihood expectation-maximization (ML-EM) algorithm with the blurring compensation method was used for image reconstruction. The calibration method was first validated by computer simulations and then implemented in the prototype system.
Data Generation (Computer Simulation)
To validate the proposed method, we simulated a dual-head SPECT system with the same geometry as that of our prototype system using the GATE (Geant4 Application for Tomographic Emission) Monte Carlo simulation tool (14,15). The Monte Carlo scripts are listed in Appendix B. The parameters of the segmented slant-hole collimator and isotope are given in Table 1. The hole diameter is the diameter of the smallest cross section of the hole, and the septum length is elongated at the outer sections accordingly. The 2 calibration steps, independent estimation and joint estimation, are performed. The goal of independent estimation is to provide initial values for the iterative solution in the joint estimation. For the independent estimation, one point source was placed at (10, 10, 20) (mm) away from the rotation center, the detector was rotated in a circular orbit, and projection data were acquired every 15° over a range of 180° at 37 s per step. The goal of the joint estimation is to further improve calibration accuracy. For the joint estimation, a high-count dataset was obtained using a long acquisition time with 2 detectors placed in a 90° configuration without any rotation. The projection matrix was acquired as 128 × 128 with a 1.25-mm2 pixel size. The image size was 64 × 64 × 64 with a 2.5-mm3 voxel size.
System Parameters
As a comparison, both the calibration results and the true parameters were used in the reconstruction of a 2-point phantom. The distance between 2 point sources is 80.0 mm.
Slant-Hole Collimator Calibration (Real SPECT System)
Our segmented slant-hole collimator was fabricated by Nuclear Fields, which provided us with a rough estimation of some parameters, as seen in Table 2. The new segmented slant-hole collimator is mounted on a dual-detector E-CAM Signature Series SPECT scanner in place of the clinical parallel-hole collimators. The diameter of the collimator hole is 1.9 mm, and the septal thickness is 0.3 mm. A point source made of a tiny drop of 3.7 MBq of 99mTc in a capillary tube was placed at an arbitrary position away from the rotation axis but in the field of view. Projections were acquired every 5° over 180°, with a total time of 21 min for the independent estimation. Just as for the Monte Carlo experiments, a set of high-count data was acquired at 0° and 90° simultaneously while keeping the setup of the system constant for the joint estimation.
Collimator Information Provided by Manufacturer
The estimated parameters were used to reconstruct the image of the point source and a heart insert with 37 MBq of 99mTc in the heart wall. The heart insert had a 2 × 2 × 1 cm cold lesion in the myocardium, and the activity in the lesion was zero. The system setup was kept the same in the whole calibration process. The projection matrix was 256 × 256, with a pixel size of 2.3976 mm.
Estimation Accuracy
The estimation accuracy can be affected by noise, correlations between the geometric parameters, and uncertainties in the estimation of the projection locations. Mean, standard deviation, and estimation error were calculated in order to evaluate the parameter accuracy. The estimation error is defined as
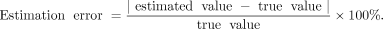 Eq. 24
Eq. 24
RESULTS
Validation (Computer Simulation)
The location of the point source estimated from section I is x 0 = 9.8 mm and y 0 = 9.3 mm. There is good agreement between the estimated location and the actual location. The error of estimation is around 0.7 mm and is well below the intrinsic resolution of the detector. On the basis of the location of the projected point source, the slant angles η and φ were estimated from each outer section and are presented in Table 3. Because of the uncertainties in measuring the center of the projected point source, the value of f varies from 226.2 to 267.0 mm. The largest estimation error of η and φ reaches 6.2% and 16.4%, respectively. A further improvement is necessary to increase the estimation accuracy. Parameters f and η were varied in a range of 10 mm and 1.5° around each mean. The value 226.2 mm, which is far from all other estimated f, was discarded. The minimum of the joint objective function was found at the parameters listed in Table 4. The difference between the estimated and actual values is less than 0.1° for the slant angles and 1 mm for the rotation radius. The estimation error is also reduced to 0.5%.
Independently Estimated Parameters with Point Source off Rotation Axis
Jointly Estimated Parameters, Giving Improved Results
Figure 7 shows the reconstruction results with estimated parameters before and after blurring correction. After blurring correction, the full-width at half-maximum (FWHM) of the reconstructed point source is reduced to 12.0 mm. The shape of the point source is well reconstructed, without any distortion. As a comparison, we also performed the reconstruction with true parameters. The reconstruction results of 2 point sources from estimated parameters and true parameters are displayed in Figure 8. The distance between 2 point sources measured from both reconstructions is 79.5 mm, which is close to the true value, 80.0 mm. In addition, no significant shape difference is observed in these 2 images.
Reconstruction results of point source without (left) and with (right) blurring correction. Five and 50 iterations were used, respectively.
Reconstruction results of 2 point sources at 50 iterations. Left one was reconstructed with true parameters. Right one was reconstructed with estimated parameters. Blurring correction was applied in both images.
Slant-Hole Collimator Calibration (Real SPECT System)
The projection of a point source is illustrated in Figure 9, which shows that the point source is elongated at outer sections along the slant angle. Table 5 lists the calibrated slant-hole parameters for each section. The location of the point source estimated from the central subdetector is at x 0 = −2.2 mm, y 0 = 42.5 mm. Figure 10 compares the image before and after calibration. Severe shape distortion is observed in the image without calibration. After calibration, a clear round shape is reconstructed. The asymmetry in the x- and y-axes is attributed mainly to the cylindric shape of the capillary tube with a 1.0-mm diameter and about a 2.0-mm axis height. The FWHM of the reconstructed point source ranges from 9.6 to 12.0 mm.
rojection of point source at 90°.
Parameters for Segmented Slant-Hole Collimator Obtained from Calibration
Reconstruction results of point source. From left to right: without calibration, with joint estimation calibration but no blurring correction, with joint estimation calibration and blurring correction. Sixty iterations were applied.
The calibrated parameters were further evaluated using the cardiac-insert phantom. Figure 11 shows the projection images of the heart phantom acquired by the stationary segmented slant-hole cardiac SPECT system. In total, 14 projection images were acquired simultaneously. Without calibration, the short-axis cut of the heart is close to a square shape and the heart wall is not uniform. With geometric calibration and resolution compensation, the “U” shape of the heart is well preserved (Fig. 12). The image is rather smooth, because correction was unable to completely remove the blurring effects. Because of the small number of view angles, the ML-EM algorithm does not completely converge to the true values when the iteration number is low. Therefore, some activity is observed in the cavity of the heart. The slice that includes the lesion is displayed in Figure 13. The lesion, which is not seen in the image without calibration, is clearly observed after calibration.
Projection of heart phantom at 0° and 90°.
Reconstruction results of heart phantom without calibration (top), with calibration but no blurring correction(middle), and with calibration and blurring correction (bottom). From left to right: vertical long-axis, short-axis, and horizontal long-axis cuts. All images were reconstructed at 80 iterations.
Slices showing defect before (top) and after (bottom) calibration. VLA cut is on left, SA cut on right. Blurring correction was applied. All images were scaled to [0 255] and were displayed using the same scale. Image contrast was enhanced for better visualization of defect. A color version of this figure is available as a supplemental file at http://tech.snmjournals.org.
DISCUSSION
In this work, we have presented a method to calibrate a stationary cardiac SPECT system that uses segmented slant-hole collimators. The calibration method consists of 2 steps. In the independent-estimation step, a closed-form solution to slant angle and rotation radius is given, and it is unique when (x 0, y 0) ≠ (0, 0). Because each section is estimated independently, a different rotation radius f is obtained for different sections, leading to an inaccurate estimation. As indicated in Table 3, the largest error in the estimation of the slant angle can reach 16.4%, greatly affecting image quality. In the second step, a joint estimation is applied for further improvement. The joint objective function is a nonlinear least-square equation that has to be solved iteratively. The solutions to the parameters in the independent estimation are used as the initial values in the joint estimation so that the proposed estimation method does not require selection of initial values. As a result, the error of estimation is reduced to less than 0.5%. In this calibration method, the point source can be placed at an arbitrary position. Errors in calibration depend on the accuracy of the measured point projection locations, which is limited by data pixel size and noise. For better calibration results, the pixel size is set as small as possible.
CONCLUSION
This paper presents a calibration method for the segmented slant-hole collimator SPECT system. This method was validated by Monte Carlo simulations and applied successfully to a conventional dual-detector SPECT system, by mounting a prototype slant-hole collimator. With the proposed 2-step calibration, the estimated parameters are accurate enough to reconstruct an image without any visible distortion.
APPENDIX A
Calculation of Projection Location and Sample Estimation
In this appendix, we explain how parameters η, φ, and f are calculated when the locations of the projected point source (u
im, v
im), (i = I,…, VII and m = 1,…, M) are known. The measured centroid (u
im, v
im) is determined as
 Eq. 1A
Eq. 1A
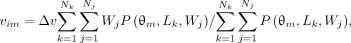 Eq. 2A
where
Eq. 2A
where
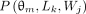 is the intensity in the projection matrix at angle θm. Here, L
k and W
j represent the pixel location in the projection matrix, and Δu and Δv are the pixel size. The location of the point source can be obtained from section I using 2 projections at 0° and 90°. Therefore,
is the intensity in the projection matrix at angle θm. Here, L
k and W
j represent the pixel location in the projection matrix, and Δu and Δv are the pixel size. The location of the point source can be obtained from section I using 2 projections at 0° and 90°. Therefore,
 ,
,
 ,
,
 .
.
Once the point source location is known, the parameters η and f have closed-form solutions given by Equations 13–15. Similarly, φ also has a closed-form solution that minimizes the objective function 7. We use
 ,
,
 , and
, and
 , i = I,…, VII, to denote the estimated parameters in the independent-estimation step.
, i = I,…, VII, to denote the estimated parameters in the independent-estimation step.
Finally, we minimize objective function 18 using an iterative method, such as the Powell method (16), and
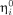 ,
,
 , and
, and
 are used as the initial values.
are used as the initial values.
APPENDIX B
Monte Carlo Simulation Code for Slant Hole
Monte Carlo code for parallel hole:
-
/gate/collimator/daughters/name hole
-
/gate/collimator/daughters/insert hexagon
-
/gate/hole/geometry/setHeight 15. mm
-
/gate/hole/geometry/setRadius .95 mm
-
/gate/hole/placement/setRotationAxis 0 1 0
-
/gate/hole/placement/setRotationAngle 90 deg
The slant hole is constructed by 4 parallelepipeds. For the slant-hole collimator, the above code is replaced by the following part:
-
/gate/collimator/daughters/name hole
-
/gate/collimator/daughters/insert parallelepiped
-
/gate/hole/geometry/setDx 1.097 mm
-
/gate/hole/geometry/setDy 0.95 mm
-
/gate/hole/geometry/setDz 15. mm
-
/gate/hole/geometry/setAlpha 30. deg
-
/gate/hole/geometry/setTheta 35.3102 deg
-
/gate/hole/geometry/setPhi 261.3274 deg
-
/gate/hole/placement/setRotationAxis 0 1 0
-
/gate/hole/placement/setRotationAngle 90. deg
-
/gate/hole/placement/setTranslation 0. 0.475 0.2742 mm
-
/gate/collimator/daughters/name hole2
-
/gate/collimator/daughters/insert parallelepiped
-
/gate/hole2/geometry/setDx 1.097 mm
-
/gate/hole2/geometry/setDy 0.95 mm
-
/gate/hole2/geometry/setDz 15. mm
-
/gate/hole2/geometry/setAlpha −30. deg
-
/gate/hole2/geometry/setTheta 35.3102 deg
-
/gate/hole2/geometry/setPhi 261.3274 deg
-
/gate/hole2/placement/setRotationAxis 0 1 0
-
/gate/hole2/placement/setRotationAngle 90. deg
-
/gate/hole2/placement/setTranslation 0. −0.475 0.2742 mm
-
/gate/collimator/daughters/name hole3
-
/gate/collimator/daughters/insert parallelepiped
-
/gate/hole3/geometry/setDx 1.097 mm
-
/gate/hole3/geometry/setDy 0.95 mm
-
/gate/hole3/geometry/setDz 15. mm
-
/gate/hole3/geometry/setAlpha −30. deg
-
/gate/hole3/geometry/setTheta 35.3102 deg
-
/gate/hole3/geometry/setPhi 261.3274 deg
-
/gate/hole3/placement/setRotationAxis 0 1 0
-
/gate/hole3/placement/setRotationAngle 90. deg
-
/gate/hole3/placement/setTranslation 0. 0.475 −0.2742 mm
-
/gate/collimator/daughters/name hole4
-
/gate/collimator/daughters/insert parallelepiped
-
/gate/hole4/geometry/setDx 1.097 mm
-
/gate/hole4/geometry/setDy 0.95 mm
-
/gate/hole4/geometry/setDz 15. mm
-
/gate/hole4/geometry/setAlpha 30. deg
-
/gate/hole4/geometry/setTheta 35.3102 deg
-
/gate/hole4/geometry/setPhi 261.3274 deg
-
/gate/hole4/placement/setRotationAxis 0 1 0
-
/gate/hole4/placement/setRotationAngle 90. deg
-
/gate/hole4/placement/setTranslation 0. −0.475 −0.2742 mm
DISCLOSURE
This work was supported by NIH grant 1R01HL108350. No other potential conflict of interest relevant to this article was reported.
Acknowledgments
We thank Dr. Roy Rowley for editing the manuscript.
Footnotes
-
Published online May 8, 2015.
REFERENCES
- Received for publication December 30, 2014.
- Accepted for publication April 3, 2015.