Abstract
An improved thresholding method for segmentation of PET volumes is proposed that uses the delineation-averaged activity concentration (AC) within an iterative procedure instead of the enclosed maximum AC. Methods: The average-based iterative thresholding method (avg-ITM) needs the background-corrected relative boundary-reproducing threshold (BRT) curve applied to segment the tumor. On the basis of a previous study, which developed an iterative thresholding method using the maximum AC (max-ITM), the average-based BRT curve was derived from the AC profiles of a sphere model. Numerous phantom scans (using glass spheres, wax spheres, and bihemispheres) under different conditions were obtained to verify and assess the avg-ITM. Clinically, the avg-ITM was tested in 2 patients bearing tumors, and the interobserver and intraobserver variability in the volume segmentation was assessed using 5 tumors analyzed by 5 observers. In the entire study, the max-ITM was also applied to compare the respective results. Results: The phantom measurements verified the average-based BRT curve and demonstrated that spheric tumors down to a diameter equaling the spatial resolution could be delineated. In contrast to the max-ITM, the avg-ITM yielded reliable volumes (within the 95% confidence intervals) for standardized uptake values and signal-to-background ratios larger than 3. The volumes derived using the max-ITM were significantly underestimated for object sizes with diameters considerably larger than the spatial resolution. Phantom measurements using bihemispheres with decreasing AC ratios demonstrated that the avg-ITM was robust down to an AC ratio of 0.5 and, therefore, is less prone to nonuniformity than the max-ITM, which was corroborated by real tumor imaging. The observer-related variability was small (mean absolute relative SD < 4%). Conclusion: Compared with the max-ITM, the avg-ITM improves the segmentation results for large objects and is less sensitive against image noise and nonuniformity. A clinical comparison study is warranted to assess the benefits of the avg-ITM method compared with other segmentation methods.
PET is of paramount importance in tumor management (1). Currently, PET scans are mainly acquired in combination with CT scans. In contrast to CT, volumes derived from PET images require an appropriate PET image segmentation algorithm. Various PET image segmentation methods have been developed, which have been described in detail in a recent survey article (2). A plethora of PET image segmentation algorithms are based on the image thresholding method. The threshold-based methodology requires the application of a relative boundary-reproducing threshold (BRT) curve to delineate the actual tumor boundary from the background. These relative BRT curves are often derived from phantom measurements using spheres of varying sizes at different (imaged) signal-to-background ratios (SBRs) (3,4). Reference (imaged) signals are often the maximum activity concentration (AC).
Phantom-based approaches have 2 main drawbacks. First, the relative BRTs for spheres with cold walls, particularly for low SBR, are considerably lower than for spheres without walls, which results in an overestimate of the volumes (3,5–7). Second, the relative BRT is defined as a percentage ratio of the (absolute) BRT to the (absolute) reference signal, and therefore, its threshold level is a function of the SBR. Thus, a relative BRT curve has to be constructed for each SBR, which requires comprehensive phantom measurements (4). These factors probably make the phantom-based approach unsuitable for the development of an easy-to-use image thresholding method.
A model-based approach was developed by van Dalen et al. (5), who used the maximum AC as a reference signal, and has been intensively used in recent studies (8–11). Only the PET spatial resolution is required to construct the relative BRT curve. Most importantly, the relative BRT is background-corrected, and its value is independent of the SBR. However, van Dalen’s algorithm, hereafter referred to as maximum-based iterative thresholding method (max-ITM), may produce imprecise results for 2 main reasons. Image noise produces a fluctuation of the maximum AC, and the presence of nonuniform uptake may affect the accuracy of the segmentation results. A more appropriate quantity is the delineation-averaged AC of the tumor.
The aim of the present study was to demonstrate that the proposed iterative thresholding method (average-based iterative thresholding method [avg-ITM]), which uses the delineation-averaged AC, improves the segmentation results compared with the max-ITM. The developed avg-ITM was verified and assessed using primarily phantom and clinical data. In the entire study, the max-ITM was also applied to compare the respective results.
MATERIALS AND METHODS
Average-Based Iterative Thresholding Method
Model-based thresholding methods require a BRT (Tbdy) to delineate the actual object boundary. Van Dalen’s methodology used the maximum AC (Imax) as the reference signal and assumed a sphere (of diameter d) surrounded by a uniform background AC (B) to construct the background-corrected relative BRT (maximum-based BRT)—that is, the ratio of (Tbdy – B) to (Imax – B). It has been shown that the maximum-based BRT does not depend on the SBR and is only a function of the ratio of sphere diameter to PET spatial resolution. In the model, the imaged activity distribution was calculated by convoluting a 3-dimensional (3D) gaussian function—its full width at half maximum (FWHM) represents the PET spatial resolution—with the true activity distribution (5,6). Similarly, it can be shown that the background-corrected relative BRT for the delineation-averaged AC (Iavg), that is, the ratio of (Tbdy – B) to (Iavg – B), is also independent of the SBR and is only a function of d/FWHM ratio. This background-corrected relative BRT ratio is denoted by Savg and is referred to as average-based BRT. Figure 1 illustrates the average-based BRT curve (Savg) and, for comparison, the maximum-based BRT curve (Smax) used in the study by van Dalen et al. (5). (Supplemental Table 1 lists selected BRT values for parameterization purposes; supplemental materials are available at http://jnm.snmjournals.org.) The formula for the BRT using the average AC is then given by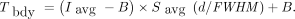 Eq. 1In the application, the avg-ITM requires initial values that are determined in the initial segmentation algorithm and are further used in the subsequent iterative thresholding segmentation algorithm. Both algorithms are described in detail in the supplemental materials. In short, the lower window level is set to zero, whereas the upper window level is sufficiently low for the tumor background to be clearly visible (Supplemental Fig. 1). To estimate the (average) background AC (B), a background volume of interest (VOI) as a 3D shell around the object is defined with sufficient distance, that is, a distance larger than or equal to the spatial resolution from the prospective object boundary to avoid contribution from the tumor signal (Supplemental Fig. 2). After the lower window level to the background AC is set, the object is delineated by drawing a VOI around the apparent object. Note that the resulting VOI is larger than the actual object size and is referred to as initial tumor VOI. The VOI analysis of the initial tumor VOI yields the initial average AC (Iinit,avg) and the corresponding initial tumor volume (Vinit).
Eq. 1In the application, the avg-ITM requires initial values that are determined in the initial segmentation algorithm and are further used in the subsequent iterative thresholding segmentation algorithm. Both algorithms are described in detail in the supplemental materials. In short, the lower window level is set to zero, whereas the upper window level is sufficiently low for the tumor background to be clearly visible (Supplemental Fig. 1). To estimate the (average) background AC (B), a background volume of interest (VOI) as a 3D shell around the object is defined with sufficient distance, that is, a distance larger than or equal to the spatial resolution from the prospective object boundary to avoid contribution from the tumor signal (Supplemental Fig. 2). After the lower window level to the background AC is set, the object is delineated by drawing a VOI around the apparent object. Note that the resulting VOI is larger than the actual object size and is referred to as initial tumor VOI. The VOI analysis of the initial tumor VOI yields the initial average AC (Iinit,avg) and the corresponding initial tumor volume (Vinit).
Theoretic average-based and maximum-based BRT curves (solid lines) and respective measured BRT values (symbols). Values within parentheses are smoothing levels used in image reconstruction.
The flowchart of the iterative thresholding segmentation algorithm is illustrated in Supplemental Figure 3. After the sphere-equivalent diameter d0 = (Vinit 6/π)1/3 is calculated, the d0/FWHM ratio is calculated and used to determine the corresponding average-based BRT value from Figure 1. Equation 1 is used to calculate the resulting threshold T1 from the initial average AC, I0,avg = Iinit,avg, that is, T1 = (I0,avg – B)⋅Savg(d0/FWHM) + B. The subscript 0 on the symbols indicates the zero-iteration step (m = 0). The initial tumor VOI is loaded, and the 3D automatic threshold procedure at T1 is applied, which produces a first-iteration tumor VOI with surface voxel values that are larger than or equal to T1. This first-iteration tumor VOI yields improved estimations for the volume, V1 or d1 = (V1 6/π)1/3, and the average AC, I1,avg. Further iterations follow until one of the following termination criteria is satisfied: the algorithm terminates either if the current volume equals the previous volume or if the segmented tumor volume is less than the minimum volume. As shown in the “Results” section, the minimum volume is an equivalent sphere with a diameter that equals the PET spatial resolution.
Uncertainty Estimation of Volume and Criterion of Acceptance
Distance measurement requires 2 points. The positional error of each point is generally half of the unit of measurement and is therefore half of the voxel length. A cubic voxel with a 1.0-mm side length is used in this study, yielding an uncertainty estimation of ±0.71 mm for the distance measurements using gaussian error propagation. These errors in the distance measurements (in the x, y, and z directions) were applied to estimate the gaussian-type uncertainty of the volume based on the geometric properties of the tumor phantoms. The range of acceptance is the 95% confidence interval (CI). Single deviations falling within this range are accepted, and those falling outside that range are unacceptable.
Tumor Phantoms
Various tumor phantoms were used and placed within the cavity of a body phantom, mimicking the patient body. The body phantom was a water-filled torso phantom described in a report by the International Eletrotechnical Commission (12). To avoid effects resulting from inactive walls, no background was used in the measurements for refillable objects.
Refillable Glass Spheres
Ten refillable glass spheres were used. The (inner) volumes were 0.15, 0.38, 0.47, 1.04, 1.69, 2.14, 2.73, 5.75, 11.44, and 26.53 mL.
Refillable Acrylic Bihemispheres
Three identical refillable acrylic bihemispheres were manufactured (volume, 25.5 mL). Each bihemisphere contained a thin plastic membrane (thickness, 50 μm) that divided the sphere into 2 hemispheres. Filling each hemisphere with a different AC was a way of simulating tumors with nonuniform activity distributions. As a result of the manufacturing process, the membrane planes did not pass exactly through the center of the sphere. This center–plane mismatch resulted in unequal hemispheric volume fractions—that is, the larger hemisphere had a percentage volume fraction of 56%.
Wax Spheres
Two radioactive wax spheres were manufactured with volumes of 0.23 and 8.09 mL and used for phantom measurements with finite background. The wax-sphere production method and the properties of the radioactive wax spheres have been described previously (13).
PET/CT System, Image Acquisition, and Reconstruction
A Biograph mCT PET/CT system (Siemens Healthcare) was used. All of the phantom scans were 1-bed-position scans, in which the phantom was placed centrally within the field of view. A high-quality and a standard clinical acquisition protocol were applied. In both protocols, a full-dose CT acquisition was applied using a 120-kVp tube voltage with an automatic tube current adjustment (Care Dose 4D, 210-mA tube current). The high-quality and standard clinical acquisition parameters (within parentheses) were as follows: a CT slice thickness of 1 mm (5 mm), a beam pitch of 1.0 (1.0), and a PET emission time range of 20–30 min (2–3 min) per bed position. The PET images were reconstructed using a 3D attenuation-weighted ordered-subset expectation maximization algorithm. Standard corrections provided by the manufacturer were performed. Unless stated otherwise, the following standard image reconstruction parameters were used: 6 iterations and 12 subsets and a postreconstruction (3D gaussian) smoothing filter of 4 mm. The CT images were reconstructed using the standard reconstruction kernel B30f. The resulting reconstructed PET and CT images had cuboid-shaped voxels of 1-mm side lengths. A small voxel size was used to avoid errors in the volumetric quantification for small volumes (discretization effect).
Phantom Study
Image Spatial Resolution at Different Smoothing Levels
The PET spatial resolution was determined at different smoothing levels (Γ). Because the AC profile of a point source, the so-called point-spread function, and the smoothing function were gaussian-shaped, the following effective spatial resolution (FWHM) is expected when convolving 2 single gaussian functions:  . R is the reconstructed spatial resolution obtained at zero smoothing level. The expected spatial resolution (FWHM) at different smoothing levels was verified by phantom measurements. Spatial resolution phantom measurements were conducted using line sources (in water) that were filled with either 18F-FDG or 124I. A thorough description and analyses have been provided in Jentzen et al. (14). The high-quality acquisition protocol was used, and images were reconstructed using a gaussian smoothing level of 0, 4, 8, and 12 mm. The PET images consisted of voxels with dimensions of 0.5 × 0.5 × 1.0 mm.
. R is the reconstructed spatial resolution obtained at zero smoothing level. The expected spatial resolution (FWHM) at different smoothing levels was verified by phantom measurements. Spatial resolution phantom measurements were conducted using line sources (in water) that were filled with either 18F-FDG or 124I. A thorough description and analyses have been provided in Jentzen et al. (14). The high-quality acquisition protocol was used, and images were reconstructed using a gaussian smoothing level of 0, 4, 8, and 12 mm. The PET images consisted of voxels with dimensions of 0.5 × 0.5 × 1.0 mm.
Verifying Average-Based BRT Curve and Spatial Resolution Effect
Ten glass spheres were filled with 18F-FDG with a prepared AC of 100 kBq/mL at the time of the PET measurements. The high-quality acquisition protocol was used. Standard image reconstruction parameters, except for the smoothing level, were used. Five smoothing levels (0, 4, 8, 12, and 20 mm) were applied. Thus, images at different ratios of diameter to spatial resolution were obtained for each sphere.
The average-based BRT values, but also the maximum-based BRT values, were experimentally determined to verify the theoretic expectation. For each spatial resolution, the BRT values (Tbdy) and ACs (Imax and Iavg) were determined for each sphere to calculate the measured maximum-based and the average-based BRT values.
The minimum diameter or volume that can be just extracted from the sphere AC profile was experimentally determined using the same phantom data. The volume of each sphere phantom was determined using the avg-ITM and max-ITM. The percentage deviation between the segmented and the actual volume was calculated and plotted against the ratio of diameter to spatial resolution. A percentage volume deviation within ±10% was considered to be acceptable.
Signal-Level Effect
The maximum AC was taken as a measure of the signal level. To evaluate the signal level effect, 2 glass spheres, a small sphere (0.15 mL) and a large sphere (26.53 mL), were filled with 18F-FDG. To obtain similar maximum ACs for both spheres, the partial-volume effect had to be accounted for. The prepared AC at the time of PET measurement was 40 and 100 kBq/mL for the largest and smallest sphere, respectively. Subsequently, 5 consecutive scans were obtained in rapid succession using the standard clinical acquisition protocol. After this first set of measurements, further 5 consecutive scans were obtained in rapid succession for each imaged maximum AC (Imax) of 32, 22, 16, and 7 kBq/mL. Both the avg-ITM and the max-ITM were applied. The maximum AC was converted into the standardized uptake value assuming a patient weight of 70 kg and an injected activity of 300 MBq of 18F-FDG.
Background-Level Effect
Two 124I-containing wax spheres with a prepared AC of 25 kBq/mL were mounted into the cavity of the torso phantom, which was filled with 18F-containing water. This phantom configuration produced a background AC that varied over time while maintaining a constant phantom signal for the object. Using the standard clinical acquisition protocol, we acquired 20 scans within 12 h with an emission time of 10 min each. An acquisition duration of 10 min was selected and not a typical emission time for a clinical setting of 2–3 min. This 5- to 3-fold increase in emission time simply compensated for the reduction in the number of positron emissions per radioactive decay (0.23 for 124I vs. 0.97 for 18F) for the same activity amount of 124I activity as 18F. The 124I settings were used in the data acquisition and image reconstruction process, and the images were reconstructed using standard image reconstruction parameters. The imaged background AC was 18 kBq/mL at the time of the first measurement. At the end of the measurement, the imaged maximum 124I ACs of the small and large wax spheres were approximately 8 and 25 kBq/mL, respectively. The avg-ITM and max-ITM were applied for each SBR to determine the volumes.
Nonuniformity Effect
The prepared AC of 18F-FDG for the larger hemisphere was 25 kBq/mL (an AC that is typically observed in tumors) and remained constant, whereas the corresponding smaller hemisphere was filled with ACs varying from 0 to 25 kBq/mL. Five consecutive scans for each hemisphere AC ratio were acquired in rapid succession using the standard clinical acquisition protocol. The images were reconstructed using the standard image reconstruction parameters. For each hemisphere AC ratio and for each single scan, the max-ITM and avg-ITM were applied to segment the bihemispheres.
Patient Study
The patients provided written informed consent for the examination, and the study was approved by the local ethics committee.
Validating Feasibility
The image data of an abdominal cancer and a thyroid cancer patient were investigated to validate the feasibility of the avg-ITM. The abdominal cancer patient underwent a standard 18F-FDG PET/CT examination (patient fasted at least 8 h, intravenous contrast agent was applied, scan was acquired 60 min after injection of 300 MBq using the Biograph mCT PET/CT system). The standard clinical acquisition protocol with an emission time of 3 min per bed position was used, and the standard image reconstruction parameters were applied. The thyroid cancer patient underwent 124I PET/MR tomography (MRT) scans (Biograph mMR; Siemens Healthcare). Scans were acquired about 24 h after capsule intake of 22 MBq. The emission time was 15 min per bed position. Simultaneous with PET, T1-weighted images were acquired using the VIBE (volumetric interpolated breath-hold examination) sequence. Standard corrections for random coincidence, dead time, attenuation (Dixon-based), and scatter were applied. PET images were reconstructed using an ordinary Poisson ordered-subset expectation maximization algorithm (4 iterations, 21 subsets). The 124I PET and MRT images had a cuboid voxel size of 2-mm side length. The measured reconstructed PET spatial resolution was 6.6 ± 0.23 mm using a 4-mm smoothing level. CT and MRT segmentations were performed manually by an experienced radiologist. The avg-ITM and max-ITMs were applied to delineate the tumors in PET.
Intra- and Interobserver Variability
The 18F-FDG image data of 5 tumors located in the neck (n = 3), back (n = 1), and axilla (n = 1) were analyzed to assess the interobserver and intraobserver variability of the segmented volumes. The cancer patients were scanned using the Biograph mCT PET/CT system; the patient protocol, acquisition, and reconstruction are described in the previous section. Five different observers applied the avg-ITM and max-ITM. One observer applied the segmentation methods 5 times for each tumor; there was at least a 1-mo interval between repeated segmentations to avoid bias.
RESULTS
Spatial Resolution at Different Smoothing Levels
The resolutions at zero smoothing level (R) were 4.20 ± 0.15 mm (18F) and 5.31 ± 0.16 mm (124I). The images that were reconstructed using the standard clinical acquisition protocol (Γ = 4 mm) had measured spatial resolutions of 5.90 ± 0.17 mm (18F) and 6.75 ± 0.18 mm (124I). The spatial resolutions at smoothing levels of 8 and 12 mm for 18F and 124I (within parentheses) were 9.22 ± 0.20 mm (9.84 ± 0.23 mm) and 12.96 ± 0.28 mm (13.52 ± 0.45 mm), respectively. The mean absolute percentage deviation ± SD between the calculated and the mean measured spatial resolution was 1.8% ± 0.2% (18F) and 2.2% ± 0.6% (124I). Hence, the calculated spatial resolution was used in all of the subsequent data analyses in this study.
Verification of Average-Based BRT Curve
Figure 1 shows the measured average-based and maximum-based BRT values at different sphere diameters. Excellent agreement was obtained for the average-based BRT values between the measurement and the theory. Similar agreement was observed for the maximum-based BRT values, except for the values that were calculated from images reconstructed at the highest spatial resolution of 4.2 mm.
Spatial Resolution Effect
The percentage differences between the segmented and true volumes at different sphere diameters (in units of the spatial resolution) are illustrated in Supplemental Figure 4. For the avg-ITM and max-ITM, the limits for reliable volume segmentation were reached when the sphere diameter approached the PET spatial resolution. Thus, the minimum diameter was equal to the PET spatial resolution.
Signal-Level Effect
Figure 2 shows the percentage differences of the segmented from the true volume at different signal levels. For the smallest sphere (Fig. 2A), the segmented volumes were well within the 95% CI even at the lowest maximum AC of 8 kBq/mL (or the lowest standardized uptake value of 3) for both the avg-ITM and the max-ITM. In contrast, unacceptable volume deviations were obtained for the largest sphere using the max-ITM (Fig. 2B). At a maximum AC range of 8–16 kBq/mL (or a standardized uptake value range of 3–5), the volumes were underestimated by 17%–22%. Even at a high signal level, the percentage volume difference (–10%) was still outside the 95% CI. The avg-ITM–based volumes of the largest sphere were almost all within the 95% CI. Hence, the accuracy of the volume properties derived for a large object (or a relatively high ratio of diameter to spatial resolution) was affected by the signal level when the max-ITM was applied but not when the avg-ITM was used.
Percentage differences between segmented and true volume (symbols) as function of signal level for small (A) and large sphere (B). Numbers within parentheses are sphere diameters in units of spatial resolution. Solid lines indicate zero percentage deviations from true volume. 95% CIs are represented by dashed lines.
Background-Level Effect
Figure 3 shows the percentage differences of the segmented from the true wax volume at varying SBRs. For the small wax sphere (Fig. 3A), the background-level effect on the segmented properties was negligible as long as the (imaged) SBR was larger than 3 for the avg-ITM and max-ITM. The volume of the largest wax sphere was underestimated systematically using the max-ITM (Fig. 3B). A difference of –10% at a high SBR or of –20% to –40% at an SBR of less than 3 was observed. In contrast, the deviations using the avg-ITM were almost all within the 95% CI.
Percentage differences between segmented and true volume (symbols) as function of SBR for small (A) and large sphere (B). Numbers within parentheses are sphere diameters in units of spatial resolution. Solid lines indicate zero percentage deviations from true volume. 95% CIs are represented by dashed lines.
Nonuniformity Effect
Figure 4 shows the percentage differences of the segmented from the true volume as a function of the hemisphere AC ratio. Changes induced by different levels of nonuniformity were measured by the (prepared) hemisphere AC ratio. The max-ITM showed volume deviations (–12%) even at a hemisphere AC ratio of unity. The volume underestimations increased rapidly as the AC ratio decreased; even worse, when one hemisphere AC was half of the other hemisphere AC, only one hemisphere volume was segmented. In contrast, the avg-ITM showed that the deviations for the complete bihemisphere volume were almost still acceptable at hemisphere AC ratios down to 0.50.
Percentage differences between segmented and true volume (symbols) as function of prepared hemisphere AC ratio using avg-ITM (A) and max-ITM (B). Gray solid lines are obtained by fitting measured data points with sigmoidal function. Upper solid line indicates zero percentage deviation from true values when both hemispheres were filled with equal AC, whereas lower solid line is expected percentage deviation from total volume when only single hemisphere contained radioactivity. 95% CIs are represented by dashed lines.
Validating Feasibility
Figure 5 illustrates the tumor boundaries and the activity distributions within the tumors. Both tumors showed obvious nonuniformity. In contrast to the avg-ITM, obvious tumor regions of relatively low activity were not delineated when using the max-ITM. For the abdominal tumor, the CT-based volume was 9.71 mL; the respective avg-ITM–based and max-ITM–based volumes were 9.64 and 6.65 mL. For the thyroid tumor, MRT-based volume was 42.34 mL; the respective avg-ITM–based and max-ITM–based quantities were 37.52 mL and 19.59 mL. Thus, the max-ITM–based PET volumes notably underestimated the volumes (–32% and –54%), whereas the avg-ITM–based volumes matched well with the morphologic volumes (–1% and –11%).
18F-FDG PET/CT transverse views of abdominal tumor (left; A, C, and E) and 124I PET/MRT transverse views of thyroid tumor (right; B, D, and F). Red lines indicate tumor boundaries. (A color version of this figure is available as a supplemental file online at http://tech.snmjournals.org/.)
Intra- and Interobserver Variability
Supplemental Table 2 lists the interobserver and intraobserver variability of the segmented volumes (tumor volume range, 0.5–4.0 mL). The observer-related variability was assessed by calculating the relative SD. The mean relative SD for the interobserver and intraobserver variability (within parentheses) was ± 3.0% (±3.5%) for the avg-ITM and ± 1.6% (±1.6%) for the max-ITM.
DISCUSSION
The max-ITM and the proposed avg-ITM rely on model-based BRT curves and the measured PET spatial resolution. Figure 1 illustrates the measured and theoretic values for the average-based and maximum-based BRT curves; a good overall agreement was obtained. However, for the maximum-based BRT values, noteworthy deviations were observed at zero smoothing. This observation could be generally attributed to the fact that the maximum AC without image smoothing fluctuates more heavily than the averaged ACs. Moreover, the measured PET spatial resolution at different smoothing levels also matched well with the calculated spatial resolution. These results partly demonstrated that the underlying model assumptions were acceptable for the PET scanner used in this study.
The sphere AC profile is used as a basic element in the ITMs to determine the actual boundary of the object. A reliable segmentation is only possible when the object reaches a sufficiently large size to be detected in the shape of the AC profile—that is, a limitation that is imposed by the limited PET spatial resolution. The BRT curves (Fig. 1) show that when the object size approaches the spatial resolution, the segmented volumes are expected to be associated with larger uncertainties. This expectation can be attributed to the increase in the slopes of the BRT curves: small changes in the object size produce large changes in the BRT values. Phantom measurements with spheres confirmed this expectation (Supplemental Fig. 4). As long as the sphere diameter is larger than or equal to the spatial resolution, the maximum percentage volume uncertainties were less than 10%. The phantom measurements suggest that the ITMs can be used to segment spherelike tumors with a minimum diameter equal to the PET spatial resolution. This conclusion assumes that the counting statistics are sufficiently large and the tumor is not localized in the lungs or other parts of the body with significant motions during acquisition.
However, such a minimum volume requires a relatively small voxel size to avoid discretization errors in the volume quantification. The critical number of voxels needed for an accurate volume determination is often neglected. The computation of this number is nontrivial and highly dependent on the shape or, more precisely, on the surface-to-volume fraction of the object. For spheres, Montelius et al. (15) demonstrated by grid-based simulations that 45 cuboid shaped voxels or 4.4 voxels per sphere diameter is required to restrict the maximum relative uncertainty margin within ±10%. Thus, to avoid the discretization effect for delineating volumes down to a typical spatial resolution of 6.0 mm, a cubic voxel length of 1.4 mm is required. The smaller the cubic voxel length, the higher is the volume accuracy of the segmented objects; however, the higher is the image noise. This drawback can be compensated for using a longer emission time, for instance; however, a longer emission time is often not feasible due to, for example, patient discomfort. Thus, if image segmentation of small tumors is the primary objective, conflicting constraints must be considered to optimize the image acquisition and the reconstruction protocol in clinical application.
Theoretically, the segmented volumes derived using the avg-ITM and max-ITM should be identical within an acceptable range. This finding holds true if the tumor is sufficiently uniform and its signal-to-noise ratio is large. The avg-ITM is expected to be less prone to nonuniformity than the max-ITM. This suggestion was proven by phantom measurements using bihemispheres with decreasing AC ratios (Fig. 4) and was further proven by real tumor imaging (Fig. 5). The results conclusively demonstrated that one advantage of the avg-ITM is its decreased sensitivity to nonuniform uptake. The effects of variability in the signal and the background on the segmentation results were examined for a small and a large object under clinical conditions (Figs. 2 and 3). The max-ITM and avg-ITM produced similar results for a small object, but for a large object (even with uniform activity) the max-ITM produced significant deviations from the actual volume. In contrast, the avg-ITM produced reliable volume estimations at various AC and SBR levels, which is obviously less sensitive against image noise.
An important factor that may affect the precision (SD) and accuracy (bias) of the segmentation results is the observer-related variability. In particular, the avg-ITM requires initial quantities (3D background shell and initial AC, Supplemental Fig. 1), which are subject to interobserver and intraobserver variability. However, the errors related to the observers involved in determining the volumes of 5 real tumors were all found to be acceptable (Supplemental Table 2). Nonetheless, the manual drawing of several VOIs to initiate the iterative procedure is time-consuming. A further development would be the formulation of a semiautomatic computer-controlled procedure.
The segmented volumes derived from the max-ITM reported in this study may be compared with other recently reported max-ITM–based volumes (5,8,10). van Dalen et al. (5) analyzed 2 large liver tumors (∼20 and 40 mL) and found that the larger tumor agreed well with CT-derived volume (deviation, 5%), suggesting a relatively uniform activity distribution, whereas the smaller liver tumor showed a notable volume mismatch between PET (25 mL) and CT (17 mL). According to the authors (5), the observed volume mismatch may be associated with tumor displacement during PET acquisition. Cheebsumon et al. (8) performed simulation and phantom experiments to investigate the influence of different imaging characteristics on the segmentation results. They demonstrated that the accuracy was affected by tumor size, SBR, and noise level. For the largest sphere (37–50 mm in diameter), they observed an underestimation of approximately 10%–20%, whereas the volume of the smallest sphere (10 mm in diameter) was either underestimated or overestimated (∼±30%). These deviation ranges were similar to that of the present study (Figs. 2 and 3). Schinagl et al. (10) segmented 28 metastatic lymph nodes in patients using CT and PET images and compared the segmented with histopathologic volumes. Considerable volume underestimations were observed, in particular for large lymph nodes, which may be explained by the presence of nonuniform activity and low signal level.
Finally, several tumor-related limitations were not assessed in this study. Tumors are sometimes nonuniform and the avg-ITM is able to partially compensate for moderate nonuniformity, but a high level of nonuniformity produces imprecise segmentation results even for the avg-ITM. Sometimes tumors have irregular boundaries and irregular outgrowths into other tissues. Both ITMs and probably also other segmentation algorithms will fail for such irregular structures. Even if the tumors are smoothly shaped and can be approximated by regular geometries such as ellipsoids, there is no single BRT value that can be used to provide the contour of the actual object. As a consequence, the properties derived from tumors that strongly deviated from sphere geometry are biased. In the phantom studies, the background AC around the object was uniform. However, in real tumor imaging, a nonuniform background uptake may result, for instance, from another tumor, resulting in errors when the ITMs are applied. The tumors are assumed to be located in a region in which motion is unlikely; therefore, the ITM results may be inaccurate depending on the amount of displacements during PET acquisition. Respiratory gating may help to reduce the effect of motion on the segmentation results. An imaging-related limitation should be mentioned in this context. In this study only 1 iterative reconstruction algorithm was used and altering the reconstruction settings (i.e., in terms of the iterations and the subsets) may affect the image properties such as the noise levels and change the results. However, studies have shown that the performance of several tumor delineation methods does not depend strongly on the imaging reconstruction settings (3,8).
The overall performance comparison revealed that the avg-ITM appears to be promising. Certainly, a comprehensive clinical study is required to compare the segmentation results using the proposed avg-ITM and other segmentation algorithms applied to real tumors. For example, a clinical comparison study may involve the Fuzzy locally adaptive Bayesian method (2). This method and a recently developed image thresholding method can deal with nonuniform activity distribution (16,17). However, not only a sophisticated segmentation algorithm should be included but also simple threshold methods such as the recently recommended algorithm proposed by Frings et al. (11). Not equivalent, but similar to the proposed avg-ITM, they tried to diminish noise sensitivity using a 50% threshold of a background-corrected reference signal that is ascertained from the average AC of a sphere of 12-mm diameter. Those performance comparisons are beyond the scope of the present study and are recommendations for future research.
CONCLUSION
Compared with the max-ITM, it has been demonstrated that the avg-ITM improved the segmentation results for large objects. The algorithm’s advantages are decreased noise sensitivity and decreased sensitivity to nonuniform uptake. A clinical comparison study is warranted to assess its benefits compared with those other segmentation methods.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Acknowledgments
I thank colleagues at the University of Duisburg-Essen (Germany), who participated in the evaluation of the interobserver and intraobserver variability (Dr. Alexia-Sabine Moldovan, Dr. Andre Prochnow, Dr. Verena Ruhlmann, and Dipl.-Ing. Dietmar Wedeleid) and segmented the real tumors using the morphological images (Dr. Marcus Reinboldt). I am indebted to Manuel Bachmann for manufacturing the refillable acrylic bihemispheres. I give special thanks to M.Sc. Roel Wierts (Maastricht University Medical Center, The Netherlands) for providing comments for improvements of the manuscript.
Footnotes
Published online Feb. 5, 2015.
REFERENCES
- Received for publication January 15, 2015.
- Accepted for publication January 16, 2015.












