Abstract
The purpose is to review in a 4-part series: (i) the basic principles of x-ray production, (ii) x-ray interactions and data capture/conversion, (iii) acquisition/creation of the CT image, and (iv) operational details of a modern multislice CT scanner integrated with a PET scanner. In part 1, the production and characteristics of x-rays were reviewed. In this article, the principles of x-ray interactions and image formation are discussed, in preparation for a general review of CT (part 3) and a more detailed investigation of PET/CT scanners in part 4.
- x-ray interactions
- γ-ray interactions
- attenuation
- x-ray image formation
- x-ray detection
- screen-film x-ray detectors
- digital x-ray detectors
- CT
Diagnostic x-ray imaging relies on the attenuation of x-rays in the patient, where the transmitted x-ray beam is detected and produces a 2-dimensional image of the x-ray interactions that depict the patient’s anatomy. Methods of producing a uniform, defined beam area of x-ray fluence were detailed in part 1 of this educational series (1). In this article, an overview of x-ray interactions and mechanisms is covered in section 1, followed by the description of the attenuation of x-rays in terms of attenuation coefficients in section 2, and methods for measuring and describing the x-ray beam in section 3. Subject contrast, the consequence of differential attenuation of x-rays by the patient, is reviewed in section 4, and details of detection and display of the x-ray information are discussed in section 5.
X-RAY (AND (γ-RAY) INTERACTIONS WITH MATTER
X-ray projection imaging and CT are made possible by the relative transparency of x-rays through the body. X-rays that are transmitted through the patient without interaction (Fig. 1A) represent the primary radiation. X-ray attenuation (removal of x-rays by absorption and scattering) within the 3-dimensional patient volume contributes to subject contrast encoded in the x-ray pattern that emerges from the patient. These x-rays are intercepted by a highly absorbing detector and are converted into a corresponding 2-dimensional image, which can be displayed and viewed after appropriate image processing.
Illustrative summary of x-ray and γ-ray interactions. (A) Primary, unattenuated beam does not interact with material. (B) Photoelectric absorption results in total removal of incident x-ray photon with energy greater than binding energy of electron in its shell, with excess energy distributed to kinetic energy of photoelectron. (C) Rayleigh scattering is interaction with electron (or whole atom) in which no energy is exchanged and incident x-ray energy equals scattered x-ray energy with small angular change in direction. (D) Compton scattering interactions occur with essentially unbound electrons, with transfer of energy shared between recoil electron and scattered photon, with energy exchange described by Klein–Nishina formula.
X-ray interactions in general can result in energy deposition and, in many cases, a secondary x-ray will be present after the initial interaction. Examples of this include scattered x-rays, characteristic x-rays, and annihilation radiation. Details of the 4 basic x-ray interactions pertinent to medical x-ray applications—namely, photoelectric absorption, Rayleigh scattering, Compton scattering, and pair production—are the focus of this section.
Photoelectric Absorption
X-rays and γ-rays not only exhibit “wave” properties like all frequencies of electromagnetic radiation (part 1 of this series) but also exhibit discrete “particle” characteristics as described by quantum mechanics (thus, the word “photon”). Photoelectric absorption involves the interaction of an incident x-ray photon with an inner shell electron in the absorbing atom that has a binding energy similar to but less than the energy of the incident photon. The incident x-ray photon transfers its energy to the electron and results in the ejection of the electron from its shell (usually the K shell) with a kinetic energy equal to the difference of the incident photon energy, E0, and the electron shell binding energy, EBE, as shown in Figure 1B. The vacated electron shell is subsequently filled by an electron from an outer shell with less binding energy (e.g., from the L or M shell), producing a characteristic x-ray equal in energy to the difference in electron binding energies of the source electron shell and the final electron shell. If the incident photon energy is less than the binding energy of the electron, the photoelectric interaction cannot occur, but if the x-ray energy is equal to the electronic binding energy (E0 = EBE), the photoelectric effect becomes energetically feasible and a large increase in attenuation occurs. As the incident photon energy increases above that of the electron shell binding energy, the likelihood of photoelectric absorption decreases at a rate proportional to 1/E3. The K absorption edge refers to the sudden jump in the probability of photoelectric absorption when the K-shell interaction is energetically possible. Similarly, the L absorption edge refers to the sudden jump in photoelectric absorption occurring at the L-shell electron binding energy (at much lower energy). After photoelectric interaction, ionization of the atom occurs and a free (photo) electron and a positively charged atom are produced. Kinetic energy (motion) of the ejected photoelectron can cause further electron–electron ionization, with most energy locally deposited. Also, a subsequent cascade of electron transitions to fill the vacated inner electron shell results in emission of characteristic radiation. Tissues in the human body contain mostly low atomic number elements (e.g., hydrogen, Z = 1; carbon, Z = 6; nitrogen, Z = 7; and oxygen Z = 8), which have low K-shell binding energies, and the “yield” of characteristic x-ray production for Z < 10 is close to zero. Auger electron events predominate in these elements. Thus, for photoelectric absorption in tissues, the energy of the incident photon is locally deposited (resulting in effectually “total” absorption). However, for compounds comprised of higher atomic number elements (e.g., iodine, Z = 53 and gadolinium, Z = 64 used for contrast agents and detector materials, respectively), the K-shell binding energies are high (e.g., 33.2 and 50.2 keV). The resultant characteristic x-rays have relatively high energy (e.g., 28.6–32.3 and 43.0–48.7 keV) and can propagate a significant distance away or completely escape the local point of interaction.
The probability of photoelectric absorption, commonly denoted as the symbol τ, is proportional to the cube of the atomic number of the interacting atom and inversely proportional to the cube of the energy, as Z3/E3. Photoelectric interaction is more likely to occur with higher atomic number elements and lower x-ray energies. As an example, the relative photoelectric absorption probability for the same thickness of iodine (Z = 53) and soft tissue (effective Z = ∼7.5) at a specific energy is approximately (53/7.5)3 = 350 times greater. Similarly, a 50-keV compared with a 100-keV x-ray photon is 1/(50/100)3 = 8 times more likely to interact by photoelectric absorption. These interaction dependencies have ramifications, such that larger x-ray transmission differences in patient anatomy occur at low energies, which enhance signal contrast. This also means that contrast agents, x-ray detectors, and protection devices are preferably made of high Z elements, such as iodine, gadolinium, and lead, respectively.
Rayleigh Scattering
An incident x-ray photon can interact with an electron and be deflected (scattered) with no loss in energy. This process is also known as coherent or elastic scattering, and it occurs by temporarily raising the energy of the electron without removing it from the atom. The electron returns to its previous energy level by emitting an x-ray photon of equal energy but with a slightly different direction, as illustrated in Figure 1C. Most x-rays are scattered forward by this mechanism, because the atom cannot experience significant recoil without otherwise removing the electron. There is no absorption of energy, and the majority of the x-ray photons are scattered with a small angle. The probability of Rayleigh scattering is given the symbol σcoh or σR. In soft tissue, probability of this event occurring is low, on the order of ∼5% of all scattering events, because of the low effective atomic number of soft tissues (Z = ∼7.5). The possibility of Rayleigh scattering increases with increasing Z of the absorbed and decreasing x-ray energy.
Compton Scattering
Compton scattering is an inelastic interaction between an x-ray photon of energy E0 that is much greater than the binding energy of an atomic electron (in this situation, the electron is essentially regarded as “free” and unbound). Partial energy transfer to the electron causes a recoil and removal from the atom at an angle, φ. The remainder of the energy, ES, is transferred to a scattered x-ray photon with a trajectory of angle θ relative to the trajectory of the incident photon (Fig. 1D). While the scattered photon may travel in any direction (i.e., scattering through any angle θ from 0° to 180°), the recoil electron may only be directed forward relative to the angle of the incident photon (>0° to ∼90°). Because of the physical requirements to preserve both energy and momentum, the energy of the scattered photon relative to the incident photon for a photon scattering angle θ is given by the equation:
This is known as the Klein–Nishina equation, where 511 keV is the energy equal to the rest mass of the electron. Qualitatively, this equation shows that the scattered x-ray energy becomes smaller as the scattering angle increases and, at higher incident energies, this effect is amplified. At very low energies (∼5 keV), the x-ray photons are preferentially backscattered; at intermediate energies (∼20 keV), the x-ray scatter distribution is approximately isotropic (equal in all directions); and at higher energies (∼60 keV), the scatter is more forward peaked, and significantly so at incident photon energies above 200 keV as shown in Figure 2. Compton scattered x-rays can deleteriously affect image quality by reducing contrast and are implicated for environmental radiation protection concerns.
Plot of scatter distribution probability as function of angle relative to incident photon direction. Three energies (20, 80, and 140 keV) show relatively isotropic distribution (in all directions) of scatter at low energies becoming more forward peaked (smaller scatter angle) at high energies.
Because the Compton scatter interaction occurs with free electrons, the probability of interaction, commonly given the symbol σ, is proportional to the electron density of the material. Except for hydrogen (which, in its most common state, does not contain a neutron in the nucleus), the number of electrons per unit mass is roughly constant due to the equal number of protons and neutrons in the nucleus, decreasing slowly for larger atomic number elements as stability requires a greater number of neutrons, and thus a larger mass for a given number of electrons. Within the diagnostic x-ray energy range (10–150 keV) the probability of Compton scatter interactions is nearly independent of energy, although at higher energies, the probability decreases as approximately 1/E0.
How much energy is absorbed locally by the Compton scatter interaction? At low energies, a large fraction of the incident energy is carried away by the scattered photons, but as the energy increases, a greater energy fraction is transferred to the recoil electron. At energies well beyond diagnostic imaging, a photon of ∼1.5 MeV, for example, shares energy equally between the scattered photon and local energy absorption.
Pair Production
Pair production can occur when the incident x-ray or γ-ray photon has energy greater than 1.02 MeV, which represents the rest mass energy equivalent of 2 electrons (i.e., E = 2 m0c2, where m0 is the rest mass of the electron [9.11 × 10−31 kg] and c is the speed of light [3.0 × 108 m/s]). The interaction of the incident photon with the electric field of the nucleus results in the production of an electron (e−)–positron (e+) pair, with any photon energy in excess of 1.02 MeV being transferred to the kinetic energy of the e−/e+ pair equally. Interestingly, ionization of the atom does not occur, although charged particles are formed and their kinetic energy can result in subsequent ionization within the local area. Once the positron expends its kinetic energy, it will combine with any available electron and produce annihilation radiation, resulting from the conversion of the rest mass energies of the e−/e+ pair into (nearly) oppositely directed 511-keV photons. The probability of pair production, commonly given the symbol π, increases with energy above 1.02 MeV. Though annihilation radiation is crucial for PET, pair production occurs at energies well above those used for diagnostic x-ray imaging.
ATTENUATION COEFFICIENTS
Linear Attenuation Coefficient
The interaction mechanisms discussed here combine to attenuate the incident photon beam as it passes through matter, through the removal of x-ray photons from the x-ray beam either by absorption or scattering events. For a monoenergetic beam of No photons incident on a thin slab of material of thickness x with a probability of attenuation, μ, the fractional reduction of the number of photons from the beam is constant, as shown in Figure 3. An exponential relationship exists between the incident and transmitted photon fluence (number of photons/mm2 area) after passing through a total material thickness, x, of an attenuating material, as:
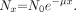The unit of thickness is commonly expressed in centimeters, so the corresponding unit of μ is cm−1, where μ is the linear attenuation coefficient, which represents the probability of attenuation per centimeter of a material. The total linear attenuation coefficient is the sum of the linear attenuation coefficients for the individual interaction mechanisms, as: μ = τ + σR + σ + π. Like the individual interaction coefficients, values of μ are strongly dependent on incident x-ray energy and on the physical density of the interacting medium. The images that CT scanners produce are in fact maps of the spatially varying linear attenuation coefficients of the tissues being scanned.
Monoenergetic x-rays are transmitted through several layers of an attenuator with attenuation coefficient, μ, of 20% per unit thickness. Attenuation occurs exponentially, as illustrated by plot (bottom left) of primary x-rays transmitted as function of attenuator thickness. On semilogarithmic plot (bottom right), exponential curve is straight line for monoenergetic x-ray beam.
Mass Attenuation Coefficient
At a given photon energy, the linear attenuation coefficient can vary significantly for the same material if it exhibits differences in physical density. A classic example is water, water vapor, and ice. The mass attenuation coefficient, μ/ρ, compensates for these variations by normalizing the linear attenuation by the density of the material. By doing so, the mass attenuation coefficients for water, water vapor, and ice are identical. For the mass attenuation coefficient, “thickness” becomes the product of the density and linear thickness of the material, or ρx. This is known as the mass thickness with units of g/cm3 × cm = g/cm2. The reciprocal of the mass thickness represents the units of mass attenuation coefficient, cm2/g, and the corresponding Lambert–Beers equation is:
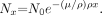Just like the total linear attenuation coefficient, the mass attenuation coefficient for a specific material is a sum of the individual interaction probabilities:
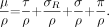
Mass Transfer and Mass Energy Coefficients
Attenuation per se is not a direct measure of the amount of energy imparted to the medium, because in most instances some of the energy of the incident photon is transferred away from the site of interaction by scattered x-rays or other energy transfer mechanisms. Knowledge of the energy transfer is important for determination of radiation dose to the tissues as well as the signal captured by an x-ray detector. The mass energy transfer coefficient, μtr/ρ, describes the amount of energy transferred to charged particles within the medium at the site of interaction and takes into account radiative losses (if any) caused by characteristic radiation emitted after photoelectric absorption and for x-ray scatter emission after the Compton scatter interaction. The mass energy absorption coefficient, μen/ρ, additionally considers the probability of energetic recoil electrons interacting within the medium and creating bremsstrahlung radiation (created in the same way as energetic electrons interact in the target of the x-ray tube to produce x-rays) that can radiate away from the site of interaction. Re-emission of bremsstrahlung energy mainly occurs with recoil electrons having high kinetic energies and with high-Z absorbers. Within the diagnostic imaging energy range, the mass energy and mass transfer coefficients are approximately equal, μen/ρ ≈ μtr/ρ. Further details about energy transfer and energy absorption coefficients are described elsewhere (2–5).
Attenuation Coefficients for Compounds
Attenuation coefficients for compounds (materials comprised of ≥2 elements) can be determined as the weighted average (by mass) of the individual mass attenuation coefficients of the compound’s constituent elements, as:
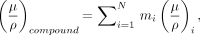where mi is the mass fraction (fraction of the element’s mass contribution to the total mass) and (μ/ρ)i is the mass attenuation coefficient of element i in the compound. This is important for estimating attenuation probabilities of compounds and materials that cannot be easily measured and particularly for computer simulations.
Attenuation Coefficient Dependencies
The mass attenuation coefficients for fat, soft tissue, bone, iodine, and lead are shown in Figure 4. Prominent on the lead attenuation curve are the L-edge and K-edge absorption discontinuities at 13–16 keV and 88 keV, respectively, and the iodine curve shows the K-edge at 33 keV. The relationships of atomic number, density, and energy are summarized in Table 1.
Mass attenuation coefficient (μ/ρ) of several materials encountered in diagnostic x-ray imaging are illustrated as function of energy. From these plots it can be determined that mass attenuation decreases at a rate of approximately 1/E3 for low energy (∼10 to ∼100 keV) and increases as a function of atomic number (Z) of attenuating material as approximately Z3. With higher Z, presence of “absorption edges” results from increased attenuation of x-rays by photoelectric absorption event at energies equal to binding energies of electrons in the specific element.
Summary of X-Ray–γ-Ray Interactions
X-RAY BEAM ATTENUATION
Measurement of X-Ray Intensity
Discussion to this point has considered single x-ray photon energies but, as described in the first article of this series on x-ray production, x-ray tube output is polyenergetic, and a spectrum of x-rays is generated as a result of the bremsstrahlung process. Determination of the attenuation properties of an x-ray beam requires that the intensity of the beam is a quantifiable attribute. Measurement of the x-ray beam intensity is performed using ionization chamber dosimeters, which are comprised of electronics, a voltage source, and separate air-filled chambers of known volume. Within the ionization chamber, electrodes collect and measure electronic charges arising from the x-ray–induced ionization of air molecules within the chamber. The average amount of energy transfer necessary to ionize an air atom and produce an ion pair (a negative electron and positive atom) is about 33 eV. X-ray exposure is a measure of the number of electron charges (ion pairs) liberated in a specific mass of air. The unit for x-ray exposure is the roentgen (R) and is equal to 2.58 × 10−4 C/kg air, where the coulomb is the basic unit of electrical charge, equal to the charge of 6.24 × 1018 electrons. When a polyenergetic beam of x-rays interacts in the air volume contained within the ionization chamber, the number of ion pairs produced is directly related to the x-ray intensity (the number of x-rays contained in the beam weighted by their x-ray energy). Collection of the ionized electrons occurs at the positive electrode (+300 V), which is centered in the air chamber. The resulting electrical charge collected during an x-ray exposure can be accurately measured and calibrated to directly read in units of integrated exposure (e.g., R) or exposure rate (e.g., R/s, mR/h). Approximately 4.13 × 1015 ion pairs (electrons) are released in 1 kg of air for an exposure equivalent to 1 R. The density of dry air at standard temperature and pressure (295° K and 1 atm) is ∼1.25 mg/cm3, and in a 1-cm3 volume, ∼4 × 109 electrons are collected per roentgen. This represents a current, if collected in 1 s, of ∼0.65 × 10−9 A or 0.65 nA. A typical volume for an ionization chamber measuring x-ray tube output intensity is ∼6 cm3, and larger volumes (e.g., 150–1,500 cm3) are required for measuring lower x-ray intensities such as beam transmission through an object and scatter measurements. In the international system of measurements, the unit for measuring x-ray intensity using an air ionization chamber is air kerma (kinetic energy released in matter), with units of milligray (mGy). There are 8.73 mGy of air kerma per roentgen of exposure.
Radiation dose is a measure of the absorbed energy per unit mass—for example, in J/kg (1 Gy = 1 J/kg). For x-ray exposure, the skin dose to the patient (in mGy) is about 10% less than the air kerma measured by an ionization chamber (in mGy). Patient radiation dose in x-ray projection imaging, CT, and nuclear medicine will be discussed in the next educational articles on CT and PET/CT.
Accurate measurement of x-ray beam attenuation needs to exclude scattered radiation, and this requires the use of so-called “good geometry.” Good geometry makes use of strict collimation of the x-ray beam such that the beam is limited to just outside the active chamber volume. The chamber also needs to be positioned a distance from the attenuator (e.g., >20 cm) to reduce and preferably eliminate scattered x-rays from reaching the ion chamber (2).
Half-Value Layer (HVL)
Unlike the discrete energies of γ-rays emitted from radioactive materials, the x-ray beam consists of a spectrum of energies over an energy range determined by the peak kilovoltage (kVp), the generator waveform, and the amount of inherent and added filtration. Lower energy photons in the spectrum are more readily attenuated, which results in a gradual shift to higher energies in the transmitted beam as it passes through an attenuating material such as aluminum on tissue, as shown in Figure 5. The gradually increasing average energy produces a corresponding decrease in the average attenuation coefficient of the transmitted beam, and thus there is an upward curvature on a semilogarithmic plot (Fig. 6). Directly measuring an x-ray spectrum in the field is impractical, but an estimate of the spectral distribution of x-rays and the relative penetrability or quality of the beam are useful. Transmission measurements of intensity through a series of attenuator thicknesses (e.g., aluminum) can characterize the beam quality in terms of the HVL. The HVL is the thickness of an attenuator required to reduce the initial beam intensity by one half, or by a factor of 2. The HVL is measured under good geometry conditions with an ionization chamber and a set of known filter thicknesses (typically) of aluminum. The relationship between the measured HVL (in mm Al) and the corresponding effective attenuation coefficient of a polyenergetic x-ray beam is determined as:
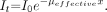Substituting x = HVL when It/I0 = 0.5:
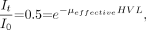and solving for μeffective gives:
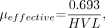where It is the transmitted intensity, I0 is the unattenuated intensity 0.693 ≈ ln(2), x is the attenuator thickness, and μeffective is the “effective” linear attenuation coefficient of the attenuator material for the polyenergetic beam. The effective energy of the polyenergetic spectrum is that which a monoenergetic beam with the same linear attenuation coefficient has. The HVL can be determined graphically from attenuation measurements, as shown in Figure 6. On a semilogarithmic plot, monoenergetic x-ray beam attenuation will be seen as a straight line, whereas the polyenergetic spectrum will have upward curvature. This is shown for the normalized output of a 120-kVp beam and the 49.9-keV monoenergetic beam with the same HVL (7.9-mm Al). Note that the slope is equal to the attenuation coefficient. As the example in Figure 6 shows, the equivalent monoenergetic x-ray beam that has the same HVL (7.9-mm Al) as the 120-kV spectrum is 49.9 keV. Most x-ray beams have an effective energy that is typically one third to one half the peak energy. As the total filtration of an x-ray tube increases, the HVL increases, μeffective decreases, and the effective energy increases. For the same amount of beam filtration, spectra produced at higher kVp will have a higher HVL. A minimum HVL for each kVp setting is required by the U.S. Food and Drug Administration (FDA) (6) to limit the radiation dose to the patient. An x-ray beam with a higher HVL will deliver less energy (and less radiation dose) to the patient for an equal transmitted intensity because there are fewer low-energy x-rays in the spectrum, and the low-energy x-rays have a higher chance of being attenuated and contributing to dose compared with the more penetrating high-energy x-rays.
Transmitted bremsstrahlung spectrum changes its energy distribution and photon fluence as result of x-ray attenuation. (Top) Curve shows 120-kVp spectrum transmitted through 0-, 5-, 10-, 15-, and 20-cm thickness of soft tissue (water), illustrating continually decreased number of photons and shift of spectrum to higher effective energy. (Bottom) Changing effective energy is more clearly shown for each transmitted spectrum normalized to peak transmitted x-ray energy in individual plots.
HVL of x-ray beam is thickness of aluminum necessary to reduce incident x-ray intensity by one half and is determined by measuring x-ray transmission as function of attenuator thickness. Depicted in 2 curves is 120-kVp spectrum measurement (solid line) and simulated monoenergetic beam (dashed line) that has same HVL. In this instance, HVL is 7.89 mm Al, and effective attenuation coefficient μeffective (cm−1) = 0.693/HVL = 0.693/0.789 cm = 0.88 cm−1. This linear attenuation coefficient corresponds to “effective” energy of 49.9 keV, determined from known mass attenuation curve of Al vs. energy, and correction for density.
Beam Hardening
Beam hardening is the term describing the shift of the transmitted x-ray spectrum to higher effective energy with increasing attenuator thickness. This is shown for 120-kVp spectra that are transmitted through 0, 5, 10, 15, and 20 cm of tissue equivalent material in Figure 5. Two characteristics are illustrated: (a) the quantity of x-rays decreases overall with greater thickness and (b) the lower energy photon fluence decreases more than the higher energy photon fluence. The degree of beam hardening is also strongly dependent on the characteristics of the attenuator. Higher Z absorbers (e.g., bone [calcium] and iodine) cause more beam hardening per unit thickness than does soft tissue, partially due to higher density (Compton scatter) and partially due to the Z3/E3 dependency of photoelectric absorption. Beam hardening can produce subtle artifacts in CT, where variations in the attenuation coefficient that occur for different x-ray paths are not compensated for in the CT image reconstruction algorithm.
TRANSMITTED X-RAY BEAM AND SUBJECT CONTRAST
The x-ray image is created by the detection of the transmitted x-rays of an incident, uniform x-ray beam that is modified by the x-ray attenuation characteristics of the object. The detected x-ray pattern is depicted as gray-scale variations in the image. Ideal x-ray image acquisition assumes a point x-ray source, a straight line trajectory from the source through the object (i.e., no scattering), and complete detection of the x-ray beam that strikes the detector. X-ray image acquisition is far from ideal, however, because of several effects explained in this section. Methods to reduce nonideal attributes and tradeoffs are also considered.
Image Geometry: Source, Magnification, and Field Variations
X-rays emanate from the focal spot of the x-ray tube. A single x-ray point source produces a diverging x-ray beam, which results in the magnification of objects that are positioned some distance from the detector (Fig. 7). The focal area can be considered as a distributed array of point sources, each producing its own view of the object, with the summation of all views creating the projection image. This geometry results in geometric blurring. This blurring is evident at the edge of an object, (the penumbra or edge gradient is often used to measure the amount of blurring) and causes a loss of object resolution even before x-rays are detected. Geometric blurring can be reduced with less magnification or with a smaller focal spot. Even with direct object–detector contact, there will still be magnification of some parts of the objects in the volume, except for a completely flat object. In CT, object magnification is a required consequence of the system geometry, where the moving detector array needs to be located a safe distance from the patient. Two focal spot sizes—“large” and “small”—are available for most general diagnostic x-ray tubes, and the selection is most often automatically determined by the tube current setting and the kVp. When imaging extremities and other relatively thin body parts, the small focal spot is the appropriate choice. For CT, the large focal spot size is required due to the high mA and long duration of the CT scan.
Image formation process from point source (A) and distributed source (B) and associated geometry terms are illustrated. By comparing similar triangles, it can be shown that M = SID/SOD. In B, blurring of object is caused by focal spot distribution incident on detector. Amount of blur, known as penumbra, increases with magnification for given focal spot size and also increases apparent magnification of object (compare Ib with I). SID = source image distance; SOD = source object distance; OID = object image distance; O = object; I = image; F = focal spot distribution; f = focal spot projection. Magnification is equal to ratio of image size to object size, M = I/O, for point source.
X-ray intensity variations caused by the heel effect (1) must also be considered when properly orienting the x-ray tube for a projection image. In the x-ray tube, electron interactions with target often occur at a depth from the surface, and x-rays projected toward the anode side of the x-ray field travel through a greater target thickness and have higher attenuation, causing a falloff of x-ray intensity compared with the cathode side. For general diagnostic imaging, the technologist has the flexibility to orient the x-ray tube and position thicker parts of the body on the cathode side of the field so that the transmitted x-ray intensity is more balanced. For example, it is prudent to orient the x-ray tube long axis parallel to the spine, with the anode side of the field directed toward the apex of the lungs, where there is less attenuation, and the cathode side directed toward the lower body and diaphragm. In CT scanners, the long axis of the x-ray tube is oriented in the slice thickness direction so that beam intensity variations occur outside of the collimated area. Variations in x-ray intensity in the direction perpendicular to the cathode–anode axis are small.
Subject Contrast and Scatter Degradation
Subject contrast is the spatial variation in the x-ray beam emerging from the patient due to x-ray attenuation resulting from x-ray interactions with the patient’s tissues; the subject contrast is thus affected by density, atomic number, and thickness properties, as shown in Figure 8. Subject contrast is enhanced with x-ray contrast agents of higher atomic number (e.g., barium salts for gastrointestinal studies, iodine for angiography) that displace lower Z materials when injected or ingested for a diagnostic examination. Without these agents, the usefulness of x-ray projection imaging or CT for evaluating stomach, intestinal tract, vascular disease, and other disorders would be limited.
Ideal projection radiograph is representation of transmitted primary x-ray fluence from point source through object and incident on detector, as depicted on left for a uniform incident fluence, I0, and transmitted I1, I2, and I3 fluences through tissue, air, and bone, respectively. Subject contrast is difference in signals of an object to background—for example, (I1 − I2)/I1 and (I1 − I3)/I1. On right is typical situation in presence of scatter, demonstrating loss of subject contrast and smaller difference between incident and transmitted radiation intensity.
Ideally, only primary radiation photons contribute to the formation of the image, and the maximum subject contrast is achieved. However, at general diagnostic imaging energies (60–140 kVp) in soft tissues and bone, a large fraction of the attenuation occurs by Compton scatter rather than by photoelectric absorption, chiefly because of the low atomic number of the tissues. X-ray scatter reduces subject contrast by adding background signals that are not representative of the anatomy. The amount of scatter increases with object thickness and field size (Table 1), and an important measurement is the scatter-to-primary ratio, S/P, indicating the scattered x-ray fluence to the primary x-ray fluence incident on the detector. In the presence of scatter, the subject contrast (primary x-rays only) is reduced by a factor equal to 1/(1 + S/P). This term is known as the contrast reduction factor. For the hypothetical case of no scatter, the subject contrast is unchanged; for S/P = 1 (equal amount of scatter to primary radiation on the detector), the subject contrast is reduced to 1/(1 + 1), or 50%; for S/P = 4, the maximum contrast is reduced to 20%. Typical S/P ratios encountered in diagnostic radiology depend on the thickness of the object, the field size, and the characteristics of the anatomy (e.g., lung, mediastinum, etc.). For a uniform scattering source, the S/P as a function of field size and thickness is illustrated in Figure 9. Scatter with conventional CT scanners is not a significant problem, because the volume of the patient irradiated at any instant is small, and the scatter is small due to tight collimation (slice thickness). However, collimation in the slice thickness direction is increasing to accommodate larger multirow detector arrays that provide multislice acquisition capability, and scatter will become a greater problem that will affect image quality and quantitative accuracy for CT images. Acceptance of scattered radiation by a detector reduces the estimate of the linear attenuation coefficient. In effect, the beam becomes “more penetrating,” not because of increased x-ray energy but because scattered radiation is detected even though it is attenuated.
Scatter-to-primary ratio at 100 kVp as function of area irradiated for 5-, 10-, 20-, and 30-cm thicknesses.
Scatter Reduction Techniques
For a given object dimension, scatter can be reduced with smaller field size (not possible in many situations), by using antiscatter grids, or implementing air gaps between the object and the detector. An antiscatter grid is a device placed between the object and the detector, composed of narrow radiopaque lead strips separated by a radiolucent interspace material (Fig. 10). The grid allows a majority of the primary x-rays to be transmitted and a majority of the scattered x-rays to be absorbed by the lead strips but, for the same incident fluence to the detector, the radiation dose to the patient must be increased by a factor of 2–3 to compensate for the loss of primary and scattered x-rays removed by the grid (the increase in exposure is known as the Bucky factor). Grids are characterized by the grid ratio (height of the lead strips to the interspace distance) and grid frequency (number of grid strips per cm). In general, higher ratio grids have an improved scatter cleanup but also have a higher Bucky factor. Grid ratios of 5:1 to 8:1 to 12:1 and focal ranges of ∼55–75 cm, ∼ 75–110 cm, and ∼150–200 cm are typically used for mammographic, fluoroscopic, and chest imaging, respectively.
Antiscatter grid, placed between patient and detector, is typically comprised of thin parallel lead strips separated by low-attenuation interspaces, as shown by cross-section illustration. Scatter is preferentially absorbed in lead strips, whereas primary x-rays will be preferentially transmitted to detector. Grid ratio is measurement of height of lead strips, h, to interspace distance, D. In general, a higher grid ratio achieves better scatter rejection but also causes a higher loss of primary radiation. The penalty of using a grid, known as the Bucky factor, is increase in dose to patient for a given x-ray fluence to detector when grid is used compared with when it is not used. The benefit of using a grid is preservation of subject contrast and improved image quality.
Air gaps (distance between the exit surface of the object and the detector) reduce scatter by allowing the more obliquely angled scattered photons emanating from the patient to propagate laterally, away from the active surface of the detector. The use of air gaps results in greater object magnification. Image magnification causes geometric blurring of edge detail, loss of object area visible on the detector, longer exposure times with greater probability of patient motion, and increased tube loading.
For CT scanner operation, a degree of scatter reduction is achieved by the relatively large air gap that is used (∼30 cm). Grid-like structures have also been used in some scanner models. Electronic scatter reduction techniques are implemented by deconvolution or other image-processing algorithms.
In nuclear medicine examinations, scatter is rejected with use of energy discrimination windows tuned to the energy of the γ-ray photons. X-ray detectors, as explained in the next section, are energy integrators, which preclude (at least with current technology) the ability to reject scatter based on its energy, and the use of broad x-ray spectrum fundamentally eliminates energy selection–based scatter removal.
X-RAY IMAGE DETECTION AND DISPLAY
Characteristics of X-Ray Detectors
X-ray subject contrast is recorded by detection of the transmitted x-ray distribution and its conversion into a visible 2-dimensional image. The ideal x-ray detector captures the transmitted x-rays with 100% efficiency, preserves the statistical integrity of the x-ray information, maps the x-ray information without any loss of resolution, and converts the locally absorbed x-ray energy into a visible light pattern on a viewing device for subsequent visualization and diagnosis. X-ray detectors are energy integrators that do not have the ability to discriminate individual detection events based on the incident photon energy. This is in part due to the polyenergetic spectrum used for x-ray imaging and CT, but mostly is due to the extremely high x-ray photon fluence (many orders of magnitude greater than γ-ray fluence from a nuclear medicine examination) that would overwhelm a detector with energy discrimination. Like nuclear medicine detectors, however, there is a need for efficient x-ray absorption, chiefly attained with detectors comprised of high atomic number elements and high density to increase the probability of attenuation by photoelectric absorption and Compton scatter interactions.
Quantum detection efficiency (QDE) of an x-ray detector describes the probability of detecting the incident radiation at a given (effective) energy, and conversion efficiency (CE) describes the transfer of absorbed x-ray energy into an amplified signal proportional to the detected x-ray fluence that is used for creating the x-ray image. The secondary signal may be light photons or electrons. High QDE is achieved with a detector comprised of high atomic numbered elements (e.g., cesium, iodine, gadolinium, tungsten) and large thicknesses. High CE for x-ray to light photons is a characteristic of the scintillator. Light-sensitive materials such as film, photomultiplier tubes, or photodiodes record the information as optical density patterns or electron charge. Direct x-ray detectors do not use light and, instead, x-ray detection leads to electron charge accumulation. X-ray information transfer to the output image is dependent on both QDE and CE.
From a statistical analysis standpoint, a more useful indicator of x-ray detector efficiency is the detective quantum efficiency (DQE), which measures the efficiency of information capture, equal to SNRout2/SNRin2, where SNRout is the signal-to-noise ratio achieved in the image, and SNRin is the signal-to-noise ratio incident on the detector, which is entirely governed by the number of incident x-ray photons. Note that DQE is not the same as QDE. One can have a very high QDE detector but, with poor CE, the secondary information will not be transferred efficiently and the DQE will therefore be low. If other sources of noise are added to the output signal (e.g., electronic noise), the DQE will decrease, even though the QDE will not change. The determination of DQE requires a sophisticated analysis of a series of digital images acquired under strictly controlled conditions. Measurement of the spatial resolution characteristics (in terms of modulation transfer function, MTF) and the noise characteristics (in terms of the noise power spectrum, NPS) is required to calculate DQE (7,8).
Analog X-Ray Detectors
The term “analog” refers to data that are continuously variable, measurable quantities, such as the brightness variations induced in an x-ray intensifying screen and the recording of the variations based on the continuous response of film (at least from a macroscopic perspective). The screen-film cassette is the most widely used analog x-ray detector for static imaging. Screen-film cassettes are comprised of an intensifying screen (a phosphor material that releases visible light when x-rays are absorbed), a light-sensitive film, and a cassette holder. Most common phosphor materials are based on gadolinium, a rare earth element (Z = 64) with a high absorption cross-section in the form of gadolinium oxysulfide (Gd2O2S:Tb), or tungsten (Z = 74) in the form of calcium tungstate (CaWO4). Usually, 2 phosphor screens mounted in a light-tight cassette are used with double emulsion films (double screens increase x-ray detection efficiency and lower radiation dose, although with a penalty of lower spatial resolution). A cross-section of a typical screen-film cassette (Fig. 11A) illustrates the absorption of incident x-rays and conversion into light. A light-sensitive film emulsion in direct contact with the screen produces a latent image, which is subsequently rendered visible by chemical processing. The result is a gray-scale image encoded by the spatially dependent accumulation of black silver grains on the plastic base. Image viewing is performed by transmitting a uniform light through the developed film, producing a 2-dimensional pattern of light in which the brightness corresponds to x-ray attenuation probability. Further details on film processing, film response, film speed, and rendering the output x-ray image in terms of spatial resolution, contrast sensitivity, and radiation dose can be found elsewhere (9).
Analog (A) and digital (B) x-ray image acquisition is depicted. In each situation, x-rays transmitted through patient and grid are detected and converted into a useful signal. Conventional analog image acquisition uses a screen-film cassette, x-rays are converted to light, latent image centers are created on film emulsion, and chemical processing renders the final output image. Because of limited latitude of the film, correct x-ray exposure during acquisition is essential. Digital image acquisition uses a detector with wide-exposure latitude to produce electronic signals that are easily converted to equivalent digital numbers by analog-to-digital converter. Once in electronic form, image processing corrects for under- or overexposure conditions and provides viewing flexibility with computer workstation.
Digital X-Ray Detectors
Digital x-ray detectors, like their analog counterparts, are designed to capture and convert the transmitted x-rays into a useful signal. The major difference between analog and digital x-ray detectors is not the detection and conversion of x-ray photons, but the digitization of the continuous output signal by discrete spatial sampling and quantization, performed by the detector and the analog-to-digital converter (ADC) as shown in Figure 11B. ADCs are specified in terms of the sampling rate (how many samples can be converted per second), which has an impact on the readout and display speed of the digital device, and the quantization step size (the minimum digital value that can express a change in the x-ray intensity variations), which has an impact on the minimum contrast resolution achievable. Spatial sampling is the division of the x-ray detector area into discrete element areas, over which x-ray information is summed. A typical sampling distance (equal to the detector element area) is about 0.1–0.2 mm for projection radiography and about 0.5 mm for conventional CT. The quantization step assigns an integer number to the signal intensity produced in the detector element area. The number of quantization steps is determined by the number of bits (binary digits) that the ADC has (the number of input and output channels). A bit represents either an off (0) or an on (1) state, and a sequence of bits (8 bits = 1 byte, 2 bytes = 1 word in a computer memory) can represent any large integer number in the base 2 numbering system (which can easily be converted to the decimal numbering system). The maximum decimal integer that can be encoded by a sequence of n bits is 2n—thus, an “8-bit” ADC can encode 28 or 256 shades of gray, and a 12-bit ADC can encode 212 or 4,096 shades of gray. Most digital radiography and CT systems in diagnostic radiology acquire data with large bit depths (12–24 bits are not uncommon) and convert those values to a range of 12 bits of data for the electronic storage and display of the image, which represents a reasonable compromise between image fidelity and digital storage and transmission efficiency.
Because digital information is discrete, a small loss of information occurs during digitization (Fig. 12A); however, the digital format provides an ability to separate the acquisition, display, and archive of images. With analog screen-film detectors, the gray-scale range of the output image is fixed and depends on the characteristics of the film response and the exposure selected by the technologist or x-ray machine. With digital images, the images can be digitally processed on a computer. Under- or overexposed images can be corrected to an appropriate gray-scale range by scaling the data (Fig. 12B). Modification of the image resolution and contrast can be achieved by postprocessing algorithms, and quantitative information is easily extracted using workstation software and display tools. Digital detectors are rapidly being deployed, with a technologic capability and overall cost that is becoming competitive with costs associated with conventional screen-film detectors and film processing.
(A) Digital x-ray image acquisition causes loss of spatial resolution by spread of object information smaller than detector element size, as shown by progressive object sizes of constant signal value and corresponding gray-level rendition. Signal modulation is depicted by MTF curves for 3 different element sizes used in diagnostic imaging. (B) Exposure latitude of film is narrow because of nonlinear response of film emulsion to chemical processing. Exposures below or above linear range of sigmoid response will not generate contrast in image. Digital detector has wide-exposure latitude, allowing various exposure levels, but image postprocessing is required to increase display contrast to appropriate level.
Display of the digital image requires the conversion of the integer values representing the x-ray image into corresponding brightness on a monitor. The digital-to-analog converter (DAC) is the electronic device that accepts digital values from each pixel as a sequence of bits into separate channels and converts them to an analog signal that drives the monitor. By rapidly sampling the digital image matrix, a “real-time” video display is produced. For a cathode ray tube (CRT), this involves producing a video voltage output combined with synchronization signals that coordinate the motion of a scanning electron beam. The current of the scanning electron beam is modulated by the voltage corresponding to the pixel values. As electrons strike on the screen phosphor in the CRT, light is emitted with a luminance determined by the electron beam current. For liquid crystal display (LCD) panels, an analog video signal can be used as input (as explained) or, alternatively, digital values can be directly input on some LCD monitors. The latter is preferred, as analog signals must be redigitized to create the image. Brightness variations are achieved by adjusting the opacity of liquid crystal elements (pixels) on the LCD panel according to digital input values at the corresponding location in the digital image matrix, and the image is produced by the differential light transmission from a high-intensity backlight. Adjustment of image brightness and contrast is performed digitally through the control of window level and window width controls, respectively, by interactively changing a conversion look-up-table (LUT) that maps input digital values into output digital values. This issue is more fully developed in the next article on CT image display.
Spatial Resolution
Spatial resolution is a measure of the detail visible in the output image. Conversion of the x-ray signal into a distribution of light photons degrades the spatial resolution, but also reduces radiation dose necessary to achieve an acceptable image. The line spread function (LSF) is a measure of the spread of signal occurring from a line source input (e.g., a “slit camera”) as shown in Figure 13. A broader LSF reduces signal contrast between small objects, until at the point they can no longer be seen. Thus, a broad LSF is characteristic of an imaging system with poor spatial resolution, whereas a narrow LSF is indicative of an imaging system with good spatial resolution. Typically the LSF is converted by a mathematic process called Fourier transformation into the MTF, a measure of the signal modulation versus spatial frequency. By definition, the modulation at 0 spatial frequency is normalized 100% or 1. A narrow LSF corresponds with a broad MTF, and both indicate good resolution transfer.
Spatial resolution degradations are caused by light spread in scintillator. Thin scintillator (top row) has small spread and correspondingly narrow LSF width with good spatial resolution, but poor x-ray detection efficiency. Thick scintillator produces large light spread distribution and broad LSF with poor spatial resolution but good x-ray detection efficiency. Combining LSF responses for x-rays spaced the same distance apart demonstrates how resolution is lost as scintillator thickness increases (Combined LSFs column), where x-axis is specified in units of distance (mm). MTF column shows inverse relationship of LSF and MTF. x-Axis for MTF is specified in units of inverse distance (mm−1).
Spatial frequency is commonly measured in units of “line-pairs” per millimeter, or lp/mm. A simple object illustrating this concept is a resolution test pattern comprised of alternating lead bars and radiolucent spaces of the same width. For instance, a spatial resolution bar pattern of 1 lp/mm consists of alternating 0.5-mm lead strips and 0.5-mm spaces, whereas 10 lp/mm consists of alternating 0.05-mm lead strips and 0.05-mm spaces. Spatial size (Δ) and spatial frequency (f) are related as: (Δ) = 1/(2 × f), demonstrating an inverse relationship between object size and spatial resolution. Losses in spatial resolution occur by focal spot blurring, pixel aperture losses, and x-ray–to–light conversion spread. With MTF analysis, these individual degradations can be combined as shown in Figure 14. Limiting spatial resolution represents the loss of signal modulation to an extent that resolvability of objects is no longer possible or useful, which is typically determined on the MTF curve at 5% modulation (0.05). A typical screen-film detector can achieve about 7 lp/mm intrinsic limiting spatial resolution, approximately equal to 0.07-mm object size, whereas a digital detector is chiefly limited by the size of the detector elements, providing about 5.0 lp/mm to 2.5 lp/mm (100- to 200-μm size). CT scanners used for clinical operations can achieve about 1.5 lp/mm (0.3 mm) limiting spatial resolution.
X-ray system is comprised of many components, each of which can degrade signal during conversion of x-rays into an image. In this example, modulation of signal is affected by focal spot blurring, pixel area averaging, and scintillator light spread as shown by individual MTF curves. Total composite system response is product of individual components at each spatial frequency. Note that total system output can be no better than the weakest component in imaging chain.
Digital Imaging Equipment
Over the past 20 y, photostimulable storage phosphor (PSP) technology, also known as computed radiography (CR), has been in service clinically. This technology closely resembles the screen-film cassette in form and function (10). Recent introduction of solid-state, direct readout detectors based on charge-coupled device (CCD) cameras and thin-film-transistor (TFT) arrays, collectively referred to as “direct radiography” or DR, are competing with CR for the eventual replacement of the screen-film detector (11). In general terms, CR requires technologist handling of the detector and subsequent processing in a CR reader device, whereas DR allows the direct acquisition and display of the digital image without additional user intervention.
The introduction of CT in 1972 (12) ushered the use of computers into diagnostic radiology (even though computers were commonplace in nuclear medicine at the time) and brought drastic technologic changes that continue today. For CT, one or more linear detector arrays are used for data acquisition, as opposed to the 2-dimensional large-field-of-view digital detectors that are used for projection radiography. The earliest CT detectors were based on sodium iodide crystals used in an energy integration mode (12) but were soon replaced with high-pressure xenon gas detectors and, subsequently, by solid-state scintillators such as cadmium tungstate and rare-earth ceramic detectors. Within the past decade, the development of continuously rotating x-ray source and detector array scanners and the recent introduction of multirow detector arrays with 0.4-s full rotation (360°) have changed the scope of CT technology. These fast scan times have brought many new clinical applications.
CONCLUSION
X-ray medical imaging is based on the differential attenuation of x-rays by intervening patient anatomy, the absorption of the transmitted x-rays by a detector, the conversion of the absorbed energy into a visible light pattern, and the subsequent processing and display of the image, either on “hard copy” analog film with a transmissive light source or on “soft-copy” video display terminals to reproduce digital image values into corresponding light patterns on a light emissive display. Because the x-ray image represents the 2-dimensional projection of a 3-dimensional object (the patient), superimposition of the anatomy along the projection direction often obscures the proper interpretation of anatomic structure and disease. The introduction of CT in 1972 was a major step toward reducing the superposition problem in diagnostic imaging. The same basic paradigm of x-ray attenuation is intrinsic in the data collection process for CT compared with projection imaging, but with one major variation: the projection data are acquired with a known angular dependence around the patient in a thin, collimated volume. Details of the equipment, acquisition, and processing used in CT to create tomographic images will be the subject of the next article in this series.
GLOSSARY
Air gap.
Distance between the exit of the patient and the detector; a method to reduce the amount of detected scatter.
Air kerma.
The kinetic energy released in air from an x-ray beam. The SI unit is typically in mGy. The exposure expressed in R is approximately equal to 8.73 mGy/R.
Analog signal.
A continuously variable signal (e.g., voltages, light intensity from an intensifying screen).
Analog-to-digital converter (ADC).
A device that converts an analog signal into a corresponding digital signal by the process of discrete temporal sampling and gray-level quantization, determined by the sampling frequency and the number of bits specified by the ADC.
Annihilation radiation.
Oppositely directed 0.511-MeV photons resulting from the conversion of the rest mass of a positive electron/negative electron pair into electromagnetic radiation.
Antiscatter grid.
A device used to selectively reduce scattered radiation from reaching the x-ray detector, usually constructed with thin, parallel lead strips and radiolucent interspaces over an area matched to the detector, and characterized by grid ratio, grid frequency, grid focal distance, and Bucky factor.
Attenuation.
The removal of x-ray photons as a result of absorption in an attenuator (via the photoelectric effect), scattering (via elastic/inelastic collisions: Rayleigh/Compton scattering), or conversion of the incident photon into an electron/positron (pair production).
Beam hardening.
An increase in the effective energy of a polyenergetic beam resulting from the preferential attenuation of the lower energy photons in the spectrum by an attenuator.
Bucky factor.
The necessary increase in dose to compensate for removing scatter and primary radiation that would otherwise produce a signal on the detector with a grid. Typical Bucky factors are from 2× to 4×, depending on the characteristics of the grid.
Charged-coupled device (CCD) camera.
A semiconductor element commonly used for electronic light detection or imaging; converts the photon energy of light to electrical charge for electronic processing
Characteristic x-ray.
A discrete x-ray with energy characteristic of the atom from which it emanates, resulting from the ejection of an inner shell (e.g., K-shell) electron by electron or photon interactions, and the subsequent filling of the shell from a transition of electrons from other shells (e.g., L-shell). The energy of the characteristic x-ray is equal to the difference in electron binding energies of the shells.
Compton scattering.
Interaction of an incident photon with an unbound electron, with partial energy transfer to the electron and scattered x-ray photon. The scatter distribution is roughly isotropic at low-to-intermediate incident photon energies (20–40 keV) and more forward peaked at higher incident energies. The interaction, commonly given the symbol σ, is proportional to the density of a material in the diagnostic energy range.
Computed radiography (CR). A 2-dimensional digital radiographic detector placed in a cassette that is composed of a photostimulable storage phosphor to detect projected x-rays. A CR reader processes the exposed phosphor to render a corresponding visible image. CR emulates the screen-film cassette paradigm closely.
Contrast degradation factor.
The maximum subject contrast available in the presence of scattered radiation, equal to: subject contrast, primary radiation/(1 + S/P), where S/P is scatter-to-primary ratio.
Conversion efficiency.
Ability of a detector to convert energy absorbed in an x-ray detector into a useful secondary signal, expressed as a fraction of the energy emitted to the energy absorbed.
Coulomb.
The amount of electric charge carried by a current of 1 A flowing for 1 s. One coulomb has 6.24 × 1018 times the charge of 1 electron.
Detective quantum efficiency (DQE).
A measure of the efficiency of information transfer, measured as a ratio of the (signal to noise)2 of the output signal relative to the ideal (signal to noise)2 of the incident radiation signal. The DQE(f) of a detector is calculated as a function of spatial frequency using MTF and NPS measurements as well as incident radiation fluence.
Digital signal.
A discrete signal, characterized by temporal sampling and quantization (conversion of signal intensity to corresponding integer values).
Digital-to-analog converter (DAC).
A device that converts a discrete digital signal into a corresponding analog signal.
Direct radiography (DR).
DR is a common term describing a self-contained digital radiographic detector that detects and converts transmitted x-rays over a 2-dimensional plane into an electronic signal and directly presents a corresponding visible image without subsequent user handling (unlike cassette-based screen-film or CR detectors).
Effective energy.
The energy of a monoenergetic beam that has the same linear attenuation coefficient of a polyenergetic beam that has been transmitted through 1 HVL of an attenuator. For example, in aluminum, μeffective (cm−1, Al) = 0.693/HVL (cm Al).
Elastic collision.
A collision between an x-ray photon and an electron that does not result in any energy loss but a change in direction of the incident photon trajectory.
Exponential attenuation.
Functional form of the removal of monoenergetic x-ray photons through an attenuator from interactions in the medium.
Focal spot.
The area on the x-ray tube anode where electrons from the cathode interact and produce x-rays.
Grid focal distance.
Distance at which orientation of the grid strips coincide with the diverging x-ray beam at a particular source-to-image distance to allow primary x-ray transmission. Focal distances of 80–100 cm and 150–190 cm are typical.
Grid frequency.
The number of lead strips per cm of distance (lines/cm). Typical values are 30–50 lines/cm.
Grid ratio.
The height of the lead strips divided by the radiolucent interspace for a parallel grid; typical grid ratios are 8:1 to 12:1 for diagnostic imaging.
Half-value layer (HVL).
The thickness of an attenuator that reduces the transmitted intensity of an x-ray or γ-ray beam by one half of the incident intensity: It = I0 when attenuator thickness = HVL.
Heel effect.
Variation of the x-ray intensity emanating from an emissive target in an x-ray tube parallel to the cathode–anode axis, where lower intensity on the anode side of the field arises from the attenuation of x-rays produced at depth that travel through a greater distance of the anode material and are more likely to be attenuated.
Inelastic collision.
A collision between an x-ray photon and an electron in which energy transfer occurs. Fractional energy transfer results in shared energy between the electron and a scattered photon, resulting in Compton scatter. Total energy transfer results in photoelectric absorption.
Ion pair.
An ionized atom (positively charged) and ejected electron (negatively charged) created as a result of energy deposition and ionization.
Ionization.
The process that results in the removal of any electron from an atom, producing an ion pair (a negative electron and a positive atom).
Ionization chamber.
An open-air chamber of known volume with collection electrodes to attract ion pairs released in the air volume and measure the corresponding charge.
K absorption edge.
A large increase in absorption of incident x-rays or γ-rays that have sufficient energy equal to or in excess of the electron binding energy of the K-shell, represented as a sharp upward edge on the attenuation curve. Energy is spent overcoming the electron binding energy, and any excess energy is transferred to the kinetic energy of the photoelectron.
Klein–Nishina equation.
Formula that relates the relationship between the scattered x-ray photon energy and the incident x-ray photon energy for a scattering angle θ.
Linear attenuation coefficient.
The probability of attenuation of an x-ray or γ-ray photon of a given energy per unit distance of an attenuator, usually expressed in units of inverse cm. The common symbol is μ.
Liquid crystal display (LCD).
A flat, visual screen that uses liquid crystal technology to display images using an array of pixels that can be made variably transmissive to a uniform backlight source according to digital pixel values.
Line spread function (LSF).
The response of a system (e.g., a radiographic detector) to a thin line source of radiation, as a distribution intensity plotted as a function of distance from the line source.
Mass attenuation coefficient.
The linear attenuation coefficient normalized by the density of an attenuator, as μ/ρ, with units of cm2/g.
Mass energy coefficient.
The probability per unit mass thickness of an attenuator that energy will be locally absorbed in the medium.
Mass thickness.
The thickness of a material that weighs 1 g and occupies an area of 1 cm2, with units that are the inverse of the mass attenuation coefficient (g/cm2).
Mass transfer coefficient.
The probability per unit mass thickness of an attenuator that energy will be transferred to the local particles in the medium.
Modulation transfer function (MTF).
A transfer function curve that plots the modulation of a signal as a function of spatial frequency. Signal blurring caused by light spread in a phosphor causes a loss of modulation, depicted by the MTF curve. The LSF and MTF are related to each other by a process known as Fourier transformation.
Noise Power Spectrum (NPS).
A spectrum of the noise contributions as a function of spatial frequency of the detector response arising from quantum (x-ray and light photons), electronic, and fixed pattern (detector nonuniformity) noise sources.
Pair production.
Creation of an electron–positron pair from the conversion of a photon with energy >1.02 MeV interacting in the vicinity of the nucleus of an atom. Subsequent annihilation of the positron results in the release of two 511-keV photons in opposite directions.
Penumbra.
Also known as the edge gradient, is the geometric unsharpness caused by a distributed focal spot and causes loss of spatial resolution. The penumbra becomes apparent and increases with magnification >1.
Photoelectric absorption.
An x-ray photon interaction with an inner shell electron that results in total absorption of the x-ray and emission of the electron. Given symbol τ, the interaction is proportional to the cube of the atomic number of the interacting atom and inversely proportional to the cube of the energy, as Z3/E3.
Photon fluence.
The number of x-ray or γ-ray photons per mm2 area.
Quantum detection efficiency (QDE).
Ability of a detector to absorb x-ray energy expressed as a fraction of the absorbed x-ray energy to the incident x-ray energy.
Rayleigh scattering.
Also known as coherent or elastic scattering, represents the change in the direction over a small angle of an incident x-ray photon interacting with an electron or the whole atom causing excitation and reemission of the photon in a different direction and without a loss of energy; given the symbol σcoh or σR.
Roentgen (R).
Unit of exposure in air equal to the release of 2.58 × 10−4 C/kg air; 1 R of exposure releases ∼1.6 × 1015 electrons in 1 kg of air.
Scatter-to-primary ratio.
Relative signal contributed by the scattered x-ray intensity to the primary x-ray intensity at a particular position from the object, usually at the position of the x-ray detector.
Screen-film cassette.
A 100-y-old technology that uses a light-sensitive film in direct contact with a high atomic number scintillator/phosphor material that fluoresces with intensity directly corresponding to the incident x-ray intensity. A latent image is subsequently rendered visible by chemical film processing, displaying high x-ray intensity areas as more opaque on the film when viewed on a light box.
Signal-to-Noise Ratio (SNR).
The peak signal relative to the SD of the noise in the background; this is different than “contrast-to-noise” or “detail signal-to-noise” ratios, which represent the difference of the signal and the background divided by the SD of the noise in the background.
Subject contrast.
The difference in the signals relative to the background generated by differential attenuation of x-rays by the patient.
Footnotes
For correspondence contact: J. Anthony Seibert, PhD, Department of Radiology, Imaging Research Center, University of California Davis, 4701 X St., Sacramento, CA 95817.
E-mail: jaseibert{at}ucdavis.edu
↵* NOTE: FOR CE CREDIT, YOU CAN ACCESS THIS ACTIVITY THROUGH THE SNM WEB SITE (http://www.snm.org/ce_online) THROUGH MARCH 2006.
