Abstract
Objective: Gamma camera nonuniformity can result in the presence of ring artifacts in reconstructed SPECT images. The objective of this study is to compare the relationship between ring artifact magnitude and image noise in tomographic images reconstructed using FBP and OSEM.
Methods: A cylindrical phantom was filled with water and 99mTc. Seven tomographic acquisitions were performed, with total counts per acquisition ranging from 1.5 Mcts to 100 Mcts. All acquisitions were reconstructed using both FBP and OSEM. Ring artifacts were generated in the transaxial data by introducing defects at a given location in each planar image. The modified acquisitions were again reconstructed using both FBP and OSEM. The ring artifacts were isolated by the subtraction of the uncorrupted datasets from the corrupted datasets. The magnitude of the ring artifacts in the corrupted reconstructions was measured and compared to the mean counts and noise level in the uncorrupted data.
Results: Ring magnitude in OSEM-reconstructed images is approximately one third that of FBP images. However, there is a corresponding reduction in image noise with OSEM and the ratio of ring magnitude-to-image noise was relatively similar for both OSEM and FBP. Rings generated with OSEM fell off more rapidly with distance from the image center, and reached a plateau at a higher magnitude at large distances. The visibility of rings with OSEM relative to FBP will depend on the location of the causative defect in the planar data and the number of iterations performed with OSEM. Differences between the 2 algorithms are subtle.
Conclusion: Our results would indicate that the uniformity requirements for SPECT are similar for FBP and OSEM reconstruction algorithms.
For the last 20 y, filtered backprojection (FBP) has been the standard technique for tomographic image reconstruction in clinical nuclear medicine. However, FBP can result in the generation of artifacts, which mainly consist of streaking and negative counts near the borders of hot objects (1,2). There are myriad iterative reconstruction algorithms that can be used as alternative reconstruction techniques to FBP. However, many of these, such as maximum likelihood expectation maximization (MLEM), are computationally intensive and have never been used in clinical practice (3). Various methods have been developed to accelerate the speed of these algorithms. The most widely used acceleration technique is the ordered subset procedure of Hudson and Larkin (4), which resulted in the development of the ordered subset expectation maximization (OSEM) technique. The OSEM algorithm recently has become available on many commercial nuclear medicine computer systems and is now being used in routine clinical practice (5,6).
The uniformity requirements for SPECT with FBP are highly dependent on the noise characteristics of the reconstructed data (7,8). There are significant differences in the noise characteristics of FBP and OSEM algorithms, particularly at low counting rates (9). While nonuniformities in the planar data would be expected to result in artifacts in the data reconstructed using OSEM, the magnitude and nature of these artifacts is not well known. Although the uniformity requirements of the FBP technique have been well studied (7,8), at present it is unclear how the uniformity requirements associated with the OSEM technique compare with those associated with the FBP technique. The aim of this study is to evaluate ring artifact magnitude and image noise in tomographic images reconstructed using the FBP and OSEM techniques. The fundamental issue addressed in this study is whether the use of the OSEM technique places different performance requirements on a SPECT system than a conventional FBP technique.
MATERIALS AND METHODS
All studies were performed on a large field-of-view dual-head gamma camera system (Varicam System, Elscint Inc., Haifa, Israel) equipped with low-energy, high-resolution collimators. A 20-cm diameter cylindrical phantom (Data Spectrum Corp., Hillsborough, NC) was filled with approximately 370 MBq 99mTc uniformly mixed in water. The phantom was positioned along the axis of rotation, with the detectors set at a radius of rotation of 15 cm. Tomographic acquisitions were performed using the following parameters: 64 × 64 word mode matrix; zoom = 2; 60 views per detector head; and every 3° over 180° gave a total of 120 views over 360°. Pixel size was 4.2 mm. A total of 7 studies were acquired, with total counts per study of 1.5, 3, 6, 13, 26, 50 and 100 million, respectively. A conventional circular orbit was used in all studies, and a high-count uniformity correction map was applied to the planar data before reconstruction or the introduction of nonuniformities to simulate ring artifacts.
Filtered Backprojection (FBP)
Transaxial slices were reconstructed into a 64 × 64 matrix using a ramp filter with cutoff at the Nyquist frequency. No data smoothing or prefiltering was applied. Attenuation correction was performed using Sorenson’s method (10). The optimum value for the attenuation coefficient was determined by measuring the coefficient of variation of counts within transaxial slices (11,12). An attenuation coefficient of μ = 0.10 cm−1 was found to give the minimum coefficient of variation.
OSEM
Raw data were converted to interfile format and transferred to a PC running the Linux operating system. The OSEM algorithm developed by Hudson and Larkin (4), which is available on the Internet (www.ocs.mq.edu.au/∼rlarkin/OSEM.html), was used. Transaxial slices were reconstructed using a subset size of 1 and between 1–50 iterations. Although in clinical practice a large subset size (e.g., 4–8) would be used to speed up the reconstruction, a subset size of 1 permits a more complete evaluation of the effect of the number of iterations on image noise and ring artifact magnitude. For OSEM with a subset size of 1, the number of iterations required to achieve good image quality is typically 30–50 (4). Unless otherwise stated, the number of iterations was set at 40 for all OSEM reconstructions in this study. Although not presented in the results below, comparable results using larger subset sizes and fewer iterations were obtained. For example, a subset size of 5 and 8 iterations yielded noise and ring magnitude results similar to those found for a subset size of 1 and 40 iterations.
Attenuation correction was performed using a mask image containing the attenuation coefficient for water. As described above, the optimum attenuation correction was again obtained with an attenuation coefficient of μ = 0.10 cm−1. No resolution recovery was performed on the data.
Ring Artifact Creation
Ring artifacts were generated in the transaxial data by introducing known defects at given locations in the planar image data. For this study, 1-pixel wide regions of interest (ROIs) were drawn on the planar data at various distances from the center of the image matrix. Seven regions were created at distances of 1.5, 4.5, 7.5, 10.5, 13.5, 16.5, and 19.5 pixels from the center of rotation. A logical AND operation was performed between the planar images and the ROIs to create a new planar dataset that only contained image data that was inside the ROIs. This dataset was then divided by a factor of 10 and added back to the original planar data to create a new set of planar images with 10% uniformity errors in the location of the ROIs. The original and corrupted planar datasets were reconstructed using both FBP and OSEM techniques. After image reconstruction, transaxial images generated from the original set of planar images were subtracted from those generated from the corrupted set of planar images to yield images containing only the ring artifacts.
The effects of acquisition orbit and multidetector acquisitions on the magnitude and shape of the ring artifacts were evaluated as follows. To simulate a 180° acquisition, data from only 1 head of the dual-detector system was used in the tomographic reconstruction. To simulate uniformity problems on 1 head of a multidetector system during a 360° acquisition, ring artifacts were introduced into the planar data from head 1, and data from both heads were used in the reconstruction. In both simulations, images showing only the ring artifacts were generated as described above.
Data Analysis
From uncorrupted transaxial images reconstructed using both FBP and OSEM, image noise was measured by drawing a circular ROI inside a uniform section of the phantom. The mean and SD of counts within the ROI were measured and the percent root mean square noise (RMS) calculated from the equation:
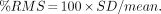
From the subtraction images (corrupted−original), the magnitude of the ring artifacts was measured from 1-pixel thick linear profiles taken through the center of the images. Ring artifact magnitude was expressed in 2 ways: as a fraction of mean counts in the corresponding original (uncorrupted) transaxial image, and as a fraction of image noise in that image.
RESULTS
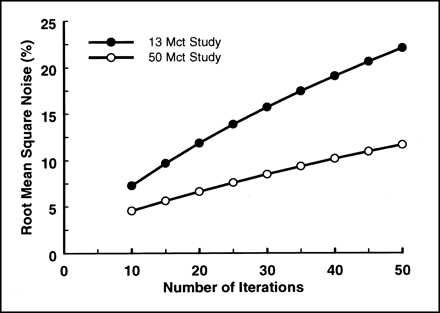
Because the visibility of ring artifacts in reconstructed transaxial images is dependent on image noise (7), it is necessary to know how image noise is affected by the type of reconstruction and the number of iterations. Figure 1 shows the effect of the number of iterations on image noise with an EM reconstruction for the 13 Mct and 50 Mct studies. Noise increased at a slightly faster rate in the 13 Mct study as compared with the 50 Mct study. Relative noise in the 13 Mct study compared with the 50 Mct study was 1.6 after 10 iterations, but increased to 1.9 after 50 iterations. Relative to FBP, image noise was a factor of 2–2.5 times lower with OSEM after 50 iterations.
Effect of the number of iterations in OSEM on percent root mean square noise in the reconstructed transaxial images for acquisitions containing 13 and 50 Mcts.
Figure 2A illustrates the relative noise levels (%RMS) in uniform transaxial slices reconstructed with FBP and OSEM as a function of total counts per study. Figure 2B shows the ratio of %RMS (FBP) to %RMS (OSEM). As the total count decreases, noise in transaxial data reconstructed with FBP increases at a faster rate than that with OSEM.
(A) Variation in percent root mean square noise in the transaxial data for images reconstructed using OSEM and FBP as a function of total counts in the acquisition. (B) Ratio of percent root mean square noise in transaxial images reconstructed with FBP and OSEM as a function of total counts in the acquisition.
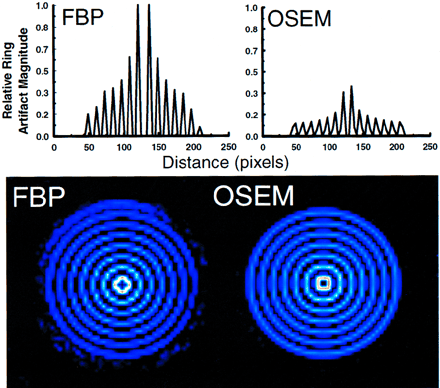
Figure 3 shows the difference between the corrupted and original transaxial slices reconstructed with FBP and OSEM, and illustrates the comparative appearance of ring artifacts with the 2 reconstruction techniques. One-pixel thick horizontal profiles taken through the center of the rings in each image are shown above. The profiles were first calculated as a fraction of mean counts in the original (uncorrupted) reconstructed transaxial images, and then normalized to the maximum value in the FBP profile. Ring magnitude with FBP is approximately 3 times that with OSEM. Rings produced by OSEM appear to be more uniform over 360° and vary less in distance from the center of the matrix than those with FBP.
Appearance of ring artifacts in FBP and OSEM reconstructions. One-pixel thick profiles taken through the center of each image are shown above. Each profile was divided by mean counts in its corresponding uncorrupted transaxial slice and expressed as a fraction of the maximum value of the FBP profile.
Figure 4 illustrates the effects of different types of acquisition orbits (dual-head 360° acquisition with errors in 180° of the data, and 180° acquisition) on the appearance of the ring artifacts with FBP and OSEM reconstructions. Differences between FBP and OSEM are comparable with those seen in Figure 3.
Appearance of ring artifacts in FBP and OSEM reconstructions for (A) top row, a 360° acquisition orbit, with corruption of data in 180° of the orbit; and (B) bottom row, a 180° acquisition orbit.
Figure 5 quantitatively illustrates the magnitude of rings formed by FBP and OSEM (40 iterations) as a function of distance from the center of rotation. In Figure 5A, results are shown relative to mean counts in transaxial slices from the 13 and 50 Mct studies. The magnitude of the ring artifact to mean counts in the transaxial slice was approximately the same for both the 13 and 50 Mct studies, and significantly large for FBP compared with OSEM. Figure 5B plots the ratio of ring artifact magnitude to percent root mean square noise as a function of distance from the center of rotation. When compared to image noise, the magnitude of the ring artifacts with FBP is only slightly larger than those with OSEM, and at large distances from the center of rotation is actually less than OSEM.
(A) Ratio of ring artifact magnitude-to-mean counts in the transaxial image for the 13 and 50 Mct studies reconstructed with FBP and OSEM (40 iterations). (B) Ratio of ring artifact magnitude-to-percent root mean square noise in the transaxial image for the 13 and 50 Mct studies reconstructed with FBP and OSEM (40 iterations).
Figure 6 shows the effect of the number of iterations with OSEM on the magnitude of ring artifacts as a function of distance from the center of rotation. To allow comparison, each ratio of ring magnitude-to-noise was normalized at 10 iterations. This graph shows the spatial dependence of ring magnitude on the number of iterations. With increasing numbers of iterations, rings of smaller diameter increase in magnitude relative to image noise. The converse is true for large diameter rings.
Ratio of ring artifact magnitude-to-percent root mean square noise in the transaxial image as a function of the number of iterations of OSEM. Each ratio of ring magnitude-to-noise was normalized to its corresponding value at 10 iterations.
DISCUSSION
With the availability of faster hardware and more efficient iterative reconstruction techniques, algorithms such as OSEM are now moving from the research environment into routine clinical use. It is important to understand the quality control requirements that such algorithms place on the imaging system. These requirements are well known for FBP, and the goal of this work is to determine the uniformity requirements for algorithms such as OSEM.
The primary attraction of OSEM compared with FBP is the absence of noise amplification (Fig. 2A). This makes OSEM the algorithm of choice for the reconstruction of low-count studies. Figure 5A shows that in the center of the field-of-view, the magnitude of ring artifacts in OSEM-reconstructed images is approximately one third that of those reconstructed using FBP. Only at the edge of the field-of-view was the ring artifact magnitude similar for both studies. However, the perception of rings in a reconstructed image is dependent not on their absolute magnitude, but rather on their magnitude relative to image noise (7). The corresponding reduction in image noise with OSEM negates much of this apparent advantage of reduced ring magnitude, and, as shown in Figure 5B, the ratio of ring magnitude-to-image noise is relatively similar for both OSEM and FBP. A close examination of Figure 5B shows that while both algorithms yield rings of similar magnitude (relative to image noise), rings generated with OSEM are consistently lower in magnitude close to the center of the image, but do not fall off with distance as rapidly as those generated with FBP. Interestingly, in Figures 3 and 4, rings generated with OSEM were slightly better delineated than those generated with FBP, possibly making them easier to detect in clinical studies. If ring artifacts are present in a clinical study, their appearance with OSEM relative to FBP will depend on the location of the causative defect in the planar data and the number of iterations performed with OSEM. While there appears to be a slight advantage to using OSEM over FBP with respect to ring artifact magnitude, this advantage is subtle; clinically, these results would indicate that the uniformity requirements for SPECT are similar for FBP and OSEM reconstruction algorithms.
To relate the above results to clinical practice, there are several additional factors that need to be addressed. The impact of spatial filters on the relationship between image noise and ring magnitude was not evaluated. A previous study on this topic (7) showed that with the application of a smoothing (Hann) filter, the ratio of ring magnitude-to-noise was essentially unchanged for artifacts created by 1–2 pixel wide defects. For larger defects (4–8 pixels wide), the ring artifacts appeared more visible (due to their lower spatial frequency) with increased smoothing. A similar effect with OSEM is anticipated.
Only the effects of 1-pixel wide defects were evaluated in this study. Because the width of the defect in the planar data affects the width of the ring artifact in the reconstructed data, but not its magnitude (7), results obtained in this study are applicable to ring artifacts created by large defects. The only consequence for large defects (4–8 pixels wide) may be the smoothing of filters. Also, the magnitude (10%) of the defects in this study is larger than that usually encountered in clinical practice. Experimentally, this study found that smaller defects gave proportionally smaller ring artifacts. A 10% defect was selected to provide more reliable ring artifacts (less noisy), but results can be scaled down to defects of a smaller magnitude. A theoretical study by Gullberg (8) has also shown ring magnitude to be directly proportional to the magnitude of the defect in the planar data.
Although this study used a subset size of 1 with OSEM, it is common to use a larger subset size to speed up the reconstruction in clinical practice. As mentioned in the methods section, comparable results were obtained for noise and ring magnitude using larger subset sizes (as many as 10) and fewer iterations (as few as 4). For example, a subset size of 5 and 8 iterations yielded noise and ring magnitude results similar to those found for a subset size of 1 and 40 iterations. Therefore, different subset sizes appear to have no significant effect on the relationship between ring magnitude and image noise, provided that an adequate number of iterations are performed.
CONCLUSION
Although the noise characteristics of OSEM and FBP are significantly different, the ratio of ring artifact magnitude-to-image noise is comparable with both reconstruction techniques. Therefore, the uniformity requirements for SPECT are not significantly influenced by the reconstruction technique. In clinical practice, the use of iterative reconstruction techniques in place of FBP does not appear to alter the basic requirements for good gamma camera uniformity.
Footnotes
For correspondence or reprints contact: Dr. M.K. O’Connor, Section of Nuclear Medicine, Charlton 1-225, Mayo Clinic, Rochester, MN, 55905; Phone: 507-284-7083; Fax: 507-266-4461, E-mail: mkoconnor@mayo.edu.