Abstract
Objective: SPECT has become a routine procedure in most nuclear medicine departments. SPECT provides significant technical challenges for the nuclear medicine technologist, as compared with planar imaging, in the areas of SPECT acquisition, image reconstruction, and data processing. Many new advances in SPECT methodology are becoming available, such as iterative reconstruction, multimodality fusion, and advanced gated cardiac SPECT. SPECT imaging is demanding and requires careful attention to proper acquisition protocols, whether circular or noncircular orbits, and postprocessing is becoming more complex with the addition of iterative reconstruction and attenuation correction algorithms, among others. Understanding the principles of SPECT is essential not only to produce the highest quality scans but also to identify image artifacts. After reading this article, the nuclear medicine technologist should be able to: (a) describe the historical development and benefits of SPECT imaging; (b) state the impact of image matrix size, number of projections, and arc of rotation on final SPECT image quality; (c) discuss the trade-offs between image noise content and spatial and contrast resolution in SPECT reconstruction; (d) discuss SPECT filters and their impact on image quality; (e) explain the differences between filtered backprojection and iterative reconstruction; and (f) describe the impact of attenuation and scatter in SPECT imaging and the advantages and pitfalls of attenuation correction methods.
- single-photon emission computed tomography
- SPECT filtering
- iterative reconstruction
- attenuation correction.
SPECT has become a routine procedure in most nuclear medicine departments since the concept was first introduced in the 1960s (1). The first single-head SPECT systems were developed in the mid 1970s using circular orbits and filtered backprojection reconstruction methods (2,3). In the 1980s, multihead SPECT systems were developed and orbits other than circular were introduced. Image reconstruction has remained filtered backprojection, until recently. As iterative reconstruction methods have improved, both in terms of reconstructed image quality and speed of reconstruction, they are now practical for routine use (4–6). SPECT scans have been viewed as slices in the transverse, sagittal, or coronal dimensions, and for cardiac applications, reoriented into oblique short- and/or long-axis slices. Using current technology, a three-dimensional representation of the organ surface or volume can be rendered and the SPECT image viewed as a truly three-dimensional object (7,8).
The advantage of SPECT imaging is that out-of-plane information is removed, not simply blurred (but present) as in earlier forms of tomography in nuclear medicine (9,10). Limited angle tomographic methods improved image contrast to some degree and provided an enhanced view of sections of the patient, but were limited by crosstalk from out-of-plane slices, and inherently were not quantitative. By removing out-of-plane information, SPECT significantly improves image contrast over planar imaging and has the ability to separate overlapping structures. Up to a 6-fold increase in image contrast can be obtained with SPECT imaging techniques, and visual interpretation of the scans benefits from this improved contrast (11,12). Spatial resolution is not improved fundamentally by SPECT scanning and the primary benefit of SPECT scanning lies in the improved image contrast. Clinically, the ability to view the reconstructed image in multiple planes and to separate overlapping structures may obviate the need for multiple images. A potential further advantage of SPECT scanning lies in improved quantification of cardiac function, for tumor/organ volume determination, and for the quantification of radioisotope uptake (13–16). Problems of gamma-ray attenuation and scatter may be better handled by SPECT (although, as yet, not completely), over planar projection imaging, as the spatial location of features and distance perspective leads to the ability to assess the amount of attenuating tissue between the skin surface and the organ of interest (17).
Improvements in SPECT technology, since the original single-head gamma camera system (which moved in a circular rotation), have included the application of multiple gamma camera heads, noncircular orbits, and the application of nonuniform attenuation correction methods. For the past 4–5 y, SPECT scans have been acquired in an ECG gated mode to assess regional myocardial wall motion and wall thickening from gated SPECT perfusion scans with 99mTc agents and, most recently, 201Tl, as well as gated SPECT blood-pool scans for enhanced assessment of global and regional ventricular function (16,18–21).
Instrumentation and software used for SPECT imaging have improved significantly in the last 20 y. SPECT scans provide additional useful information, but also require more careful attention to gamma camera and computer quality control, particularly when using multihead gamma camera systems. Awareness of the potential artifacts and anomalies that could be present in a SPECT scan due to camera/computer/gantry problems, or technical problems, is essential. This article is designed to give the reader a basic understanding of the principles of SPECT reconstruction, principles which lead to improved image contrast and quantification.
THE PHYSICS OF SPECT
SPECT Data Acquisition
Arc of Rotation.
SPECT acquisition is performed by rotating or stepping the gamma camera around the patient while acquiring data into the digital matrix of a computer at all angles sampled, as illustrated in Figure 1. According to the theory of CT, projection views acquired over only 180° of arc are required for correct reconstruction. In a perfect imaging system, projections opposite each other are essentially mirror images of each other. Thus, the opposing views are redundant, and only 1 is needed. However, the nuclear medicine gamma camera is not a perfect imaging system, therefore, opposing views are not the same. First, the resolution of the gamma camera degrades as the distance between the camera and object being imaged increases. Second, a certain percentage of Compton scatter is accepted as photopeak gamma rays, due to the finite energy resolution of the camera. Third, a certain fraction of gamma rays from an object is attenuated (absorbed) when they are emitted in an attenuating medium, such as a patient. This phenomenon varies according to the depth of attenuating medium between the object and the gamma camera. In clinical SPECT, opposing projection views will never be the same. Therefore, 360° of arc is required for accurate reconstruction in most SPECT studies.
Schematic diagram of SPECT data acquisition. For each projection view, the computer sends a message to the gamma camera to step to the next viewing angle and, after the camera sends a message back to the computer that it is ready to acquire, the computer acquires the projection image at that angle for a specified time. The actual time t required for each view is the sum of the camera step time plus the projection image acquisition time. The total SPECT study acquisition time is T = mt, where m is the number of views acquired (in this case, 60 views over 360°, at 6° intervals).
One generally accepted exception to this rule is SPECT myocardial imaging, where 180° acquisition is the standard practice. Although distortions due to variable and directionally dependent resolution across the transverse slices in 180° SPECT reconstructions will occur (22–25), they are countered by the fact that the heart is generally positioned somewhat anteriorly and to the left in the thorax. Projection views opposite the heart (i.e., LPO through RAO) see significantly less myocardial activity due to attenuation through the patient's chest. Those views contribute mostly noise and scatter to the reconstruction, degrading overall resolution and contrast. Reconstructions from 180° acquisitions will have improved resolution and contrast, at the expense of some distortion.
Matrix Size.
An important aspect of SPECT imaging is the selection of the matrix size in the computer for the projection views. Essentially, the computer divides up the gamma camera field of view (FOV) into square areas (pixels), and the 2 matrix sizes typically associated with SPECT imaging are 64 × 64 and 128 × 128, rows by columns. The choice of matrix size depends on several factors. First, the size of a pixel should, ideally, be less than 1/3 of the expected full-width at half-maximum (FWHM) resolution of the SPECT system, measured at the center of rotation for the isotope being imaged, including the effects of the collimator and the radius of rotation (i.e., distance of camera from patient). On current state-of-the-art SPECT systems, where the camera's digital FOV (with zoom = 1) is precalibrated by the manufacturer, the size of a pixel, D, in millimeters, may be calculated:
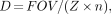 Eq. 1
Eq. 1
where:
FOV (mm) = the widest dimension of the computer image matrix
Z = zoom factor (e.g., 1.5, 2.0, etc.) during acquisition
n = number of pixels (e.g., 64 or 128).
For example, if the expected SPECT FWHM is approximately 15 mm, then the pixel size should be less than 5 mm. A 128 × 128 image will have a finer pixel resolution, hence spatial resolution, than the corresponding 64 × 64 image, as illustrated in Figure 2. For instance, a typical gamma camera might have a FOV width of approximately 400 mm across. The pixel size for a 128 × 128 matrix with no zoom would be 3.125 mm, whereas, a 64 × 64 matrix would have a 6.25 mm pixel size. If the expected resolution was 10 mm, then a 64 × 64 matrix would degrade resolution. However, since most realized spatial resolution from a SPECT system is of the order of 18–25 mm at the center of the rotation, a 64 × 64 matrix is perfectly adequate for most imaging applications. Higher SPECT resolution will always be achieved with the smaller pixel size of 128 × 128 matrices, however pixel signal-to-noise ratio may be much poorer as the counts are divided up into 4 times the pixels of a 64 × 64 matrix image covering the gamma camera FOV. For the same acquisition, a 128 × 128 image will only have 1/4 the counts per pixel as the corresponding 64 × 64 image. The noise in the reconstructed slices is complicated by the backprojection process, and does not follow simple nuclear counting statistics. A formulation for the percent noise has been given by Budinger et al. (26):
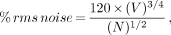 Eq. 2where:
Eq. 2where:
V = the total number of voxels covering the reconstructed object, based on a circular FOV
N = the total number of events acquired.
The 128 × 128 reconstructed percent noise will be approximately 3 times that of the corresponding 64 × 64 reconstruction.
(A) 64 × 64 and (B) 128 × 128 SPECT reconstructions of the central transverse slice from a 99mTc-HMPAO brain SPECT study. Equivalent reconstruction filtering was used (10th order Butterworth, 0.75 Nyquist for 64 × 64 and 0.375 Nyquist for 128 × 128). Not only is the resolution within each slice improved for 128 × 128, with equivalent smoothing, but the slices are only half as thick compared with 64 × 64, leading to improved resolution in the third dimension (i.e., between slices).
Finally, consider the amount of computer memory and disk space used to read, write, process, and display a SPECT study that depends on the matrix size selected. For the same number of projection views, a 128 × 128 image acquisition will consume 4 times the disk space and computer memory, and the reconstructed volume will consume 8 times the disk space and memory, as the corresponding 64 × 64 image data. In addition, the 128 × 128 image data might take on the order of 4–8 times longer to process and film. However, as technology continues to greatly improve the speed of the computer and reduce the cost of chips, memory, disks, displays, filming devices, etc., the difference in real time will eventually become insignificant. Relative memory and disk space requirements for 128 × 128 and 64 × 64 SPECT acquisitions is given in Table 1.
SPECT Acquisition Disk Space Requirements
Radius of Rotation and Number of Projections.
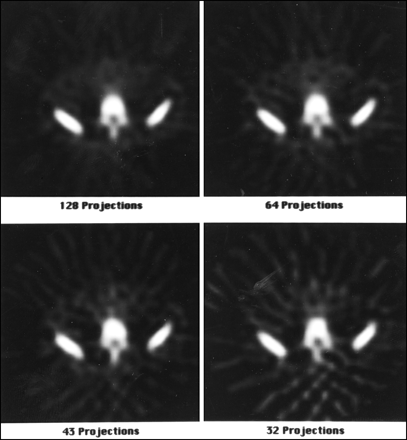
Ideally, for accurate reconstruction the number of angular views over 360° should be at least equal to the projection image matrix size (e.g., 64 views for a 64 × 64 matrix and 128 views for a 128 × 128 matrix). When the number of views is less than the minimum, streak artifacts may appear in the reconstructed slices. Figure 3 illustrates a SPECT bone scan of the lumbar spine acquired with 32, 43, 64, and 128 projections. Streaking is observed in the 32-projection image and some image quality is lost. The SPECT imaging system rotates around the long axis of the patient, who is lying on the SPECT imaging table, or pallet. The radius of rotation is adjusted so that the camera will not come into contact with either the patient's surface or the pallet. For circular orbits, this places the gamma camera head(s) far from the patient in the anterior and posterior projections. To avoid this problem, state-of-the-art SPECT imaging systems include a feature called noncircular orbit (NCO). With NCO, the gamma camera can determine an orbit, either automatically or with the aid of the technologist, which will bring the camera as close to the patient as possible at all angles, improving spatial resolution (27). Then, during the actual SPECT acquisition, the camera will move in and out radially as it rotates around the patient (hence, the name NCO, noncircular orbit).
The effect of the number of angular samples on SPECT reconstruction. A transverse slice is shown, reconstructed from the identical 64 × 64, 128-view projection set and using the identical reconstruction filter (i.e., 0.7 Nyquist, eighth order Butterworth). The number of views used was all 128 (upper left), every second view, or 64 (upper right), every third view, or 43 (lower left) and every fourth view, or 32 (lower right). The 128- and 64-view reconstructions appear quite similar and artifact free. However, note the appearance of streak artifacts in the 43- and 32-view reconstructions (more prominent as the number of angular samples decreases).
Some SPECT systems also may be capable of performing acquisitions in both the standard step-and-shoot mode and in a continuous fashion. The step-and-shoot mode consists of alternately rotating to the next view (step) and acquiring a projection with the camera stationary (shoot). Depending on the system, there may be up to several seconds of delay between the acquisition of successive views. For short acquisitions, this can be a significant source of system dead time (i.e., the system is not counting while stepping). In continuous mode, on the other hand, events are acquired during the entire camera rotation, as the camera rotates in a continuous fashion around the patient. Thus, each projection view will be somewhat blurred, or smeared, horizontally along each row of pixels. This blurring will affect, in turn, the final resolution of the reconstructed slices. The amount of blur depends on the degrees of arc over which each projection is acquired. However, it has been determined that if at least 120 views over 360° are acquired, or 3° of arc per view, then the blur is insignificant.
Basic Principles of Image Reconstruction
Image reconstruction from projections forms the basis for SPECT. SPECT projection images acquired with gamma cameras are analogous to two-dimensional photographs of a three-dimensional scene, taken from different directions. One picture, by itself, does not allow placement of objects in the scene in the real three-dimensional world, as it represents a summation of the three-dimensional scene into a two-dimensional projection. However, by taking photographs from many different directions, or angles, around the scene, the scene may be reconstructed in 3 dimensions. The projections must first be mathematically modified to reconstruct the three-dimensional distribution accurately. The traditional approach of filtered backprojection is based on a mathematical theory of image reconstruction from projections called the Radon transform, developed by the German mathematician Johann Radon in 1917, which was valid under specific conditions that are not entirely true for a SPECT imaging system (28–30). The iterative model of reconstruction, on the other hand, is based on an estimate of the actual probability of a certain amount of radioactivity at a particular location being detected by the imaging system at each particular point in each projection. Included in the iterative model are physics issues, such as the spatial resolution of the system (including variation with distance from the collimator), attenuation (e.g., from transmission source scans), and, in some incarnations, Compton scattering.
Backprojection Reconstruction and Filtering
Backprojection.
In SPECT imaging, projection views are acquired at evenly spaced angles around the long axis of the patient, resulting in images with rows and columns of equidistant sampled areas (picture elements, or pixels). Thus, the pixels represent summations of the voxels at an angle perpendicular to the camera face. In the computer, the three-dimensional volume of radioactivity representing a function of activity versus three-dimensional position in space, is viewed as a stack of two-dimensional transverse slices of thickness equal to the z dimension of a voxel, as illustrated in Figure 4. In filtered backprojection reconstruction, each row of each projection image is viewed as a one dimensional representation of the object's projection. The one-dimensional pixel profiles are modified mathematically, or filtered, and projected back across the two-dimensional slice at their respective angles (ergo backprojection). The two-dimensional profile backprojections are added together, forming the reconstructed two-dimensional transverse image.
Diagram of SPECT projection imaging process (radon transform). The gamma camera views the three-dimensional (x,y,z) object as a stack of two-dimensional (x,y) slices of finite thickness dz. The volume elements, or voxels, within each slice (shaded area) are projected onto the gamma camera image as a horizontal row of picture elements, or pixels (along X′, at a particular height along Y′). Projection images at multiple angles around the axis of rotation (z) are acquired to reconstruct the three-dimensional object.
In the image domain, SPECT reconstruction is typically discussed in terms of the mathematical process known as convolution, the mathematical description of which can become quite complicated. Instead, the mathematical basis of SPECT may be more easily understood by describing the process in the spatial frequency domain. Spatial frequencies in the case of SPECT, refer to the frequencies contained in the variation of counts corresponding to objects (organs, tumors) in the patient, for example small objects and sharp edges contain more high frequencies than do broad, flat objects. Spatial information is converted to frequency information by the mathematical process known as the Fourier transform, or FT. This process is analogous to an equalizer in a sound system. An equalizer converts the incoming sound signal into its constituent frequency bands (i.e., computes a FT), creating a frequency spectrum from the low, or bass, frequencies to the high, or treble, frequencies. One may then filter the spectrum with the equalizer by adjusting the equalizer knobs, increasing or decreasing the amplitude of certain or all frequencies contained in the original signal. The filtered frequency spectrum is finally converted back and output as a modified sound signal (the inverse FT).
The spatial frequencies of SPECT data are digitally sampled, as are the images themselves. What spatial frequencies are contained in SPECT images? The answer lies in the gamma camera system's (including collimator) ability to detect high frequencies (small objects), and how finely the data coming from the camera is sampled (number of pixels). The sampling theorem states that when data are acquired in a nuclear medicine computer matrix, the maximum spatial frequency (FN) which may be captured is given by:
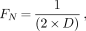 Eq. 3
where FN is the Nyquist frequency and D is the pixel size. In other words, one must sample a frequency twice per cycle to recover that frequency component. For example, if D is 6.25 mm for a 64 × 64 image, then FN is 0.08 cycles per millimeter (mm−1). For the corresponding 128 × 128 image FN is 0.16 mm−1. The dimension of FN is typically given in cycles per centimeter (cm−1), or in cycles/pixel (dimension-less), where FN is equal to 1 over 2 times pixel size. (Note that FN for 128 × 128 is always twice FN for 64 × 64).
Eq. 3
where FN is the Nyquist frequency and D is the pixel size. In other words, one must sample a frequency twice per cycle to recover that frequency component. For example, if D is 6.25 mm for a 64 × 64 image, then FN is 0.08 cycles per millimeter (mm−1). For the corresponding 128 × 128 image FN is 0.16 mm−1. The dimension of FN is typically given in cycles per centimeter (cm−1), or in cycles/pixel (dimension-less), where FN is equal to 1 over 2 times pixel size. (Note that FN for 128 × 128 is always twice FN for 64 × 64).
Filter Functions.
As discussed earlier, a three-dimensional distribution of radioactivity is reconstructed as a stack of two-dimensional transverse slices of finite thickness, through backprojection of a series of two-dimensional projections. The projection profiles are smoothed, or blurred, by the projection process. To reconstruct the original, unblurred three-dimensional distribution, the profiles must first be filtered by a function known as a linear ramp in the spatial frequency domain. The linear ramp can simply be thought of as an amplifier, with increasing amplification as the frequencies increase, boosting the ability to see small objects (higher frequency objects, a higher power telescope). The linear ramp is a necessary, compensatory filter, as it removes the blurring effect of the projection process. In clinical SPECT, however, 2 problems arise. First, due to its finite resolution, the gamma camera/collimator imaging system is a low-pass filter, reducing the amplitude of the projection profile's frequency spectrum as the frequency increases. Thus, only a smoothed version of the original three-dimensional distribution at best may be reconstructed to begin with. Second, clinical nuclear medicine images tend to be photon deficient. The Poisson statistical noise inherent in all nuclear medicine images has approximately the same amplitude at all frequencies, and is known as white noise. The Poisson statistical noise is added to the already blurred profiles, and the final result is a blurred, noisy profile.
Figure 5 illustrates the following. If the frequency spectrum was examined through the FT, it would contain: (a) a signal from the original object, blurred by the camera/collimator (which would pass primarily low frequencies, upper left); and (b) Poisson noise at all frequencies (lower left). The point along the spectrum where the signal falls to the level of the Poisson noise depends on the level of noise (which is determined by the number of counts collected) and the object frequencies passed by the gamma camera system (which depends on the collimator, patient-to-camera distance, as well as on Compton scatter), which is generally characterized as a modulation transfer function (MTF—upper right), which in simple terms, plots the amplitude at which objects of increasing frequencies are passed. As the total counts in the study increase, the noise level relative to the patient data decreases (from Level 3 to Level 1). That is why, in general, a higher number of counts in a SPECT study is better (i.e., noise dominates higher up the frequency spectrum, allowing clearer images of medium frequency (midsize) objects (cutoff at f1, rather than f3, lower right)).
(A) Original, ideal frequency spectrum of a typical one-dimensional SPECT projection profile of an object. (B) Frequency spectrum, or modulation transfer function (MTF), of the SPECT imaging system (i.e., gamma camera/collimator). (C) White noise frequency spectra for 3 levels of Poisson statistical noise (1 equals the lowest level). (D) The original profile spectrum is multiplied by the SPECT system MTF and the 3 Poisson noise spectra are added, resulting in the 3 final, modified profile spectra. The spatial frequency where the object signal falls to the level of the noise increases as the noise level decreases (i.e., as the acquired counts increase).
When backprojection is performed with the linear ramp filter, the noise, dominant at higher frequencies will be greatly amplified (recall the role of the ramp filter), and the resultant reconstructed slices will be extremely noisy and unreadable. (Imagine turning all settings on your graphic equalizer to zero except the highest frequency (10–20 kHz), which is turned to its maximum value. The high frequency “hish” would provide for unpleasant listening.). Therefore, it is necessary to cut off the linear ramp around the point where the frequencies corresponding to the patient data disappear into the noise. This is the purpose of window filter functions, examples of which are the Hamming and Butterworth filters.
In the frequency domain, the window (filter) is applied to the ramp filter. The adjective window implies that these filters are analogous to actual windows, as they are opened up to pass higher frequencies and closed to pass only lower frequencies. The cut off of the window (fc) should be the point where the noise predominates and the patient object data are minimal. A list of the standard filter functions typically available is given in Table 2. For all the window filter functions, the cutoff frequency, fc may be varied (typically 0.2–1.0 Nyquist). Many of the window functions have a shape, where the amplitude of the frequency passed varies intermediately between all pass and no pass. For the Generalized Hamming filter, the a weighting factor also may be varied (typically 0.5–1.0); for the Butterworth filter, the order also may be varied (typically 4.0–10.0). For the Butterworth filter, the higher the order, the faster the window closes. The filter fc is most often specified as a fraction of the aforementioned Nyquist frequency, FN, (the highest frequency the system is capable of reproducing). Note that for the equivalent filter, fc for a 128 × 128 matrix is 1/2 that for 64 × 64 (i.e., 0.5 Nyquist for 64 × 64 equals 0.25 Nyquist for 128 × 128).
Standard SPECT Reconstruction Window Filter Functions
The effect of the choice of window filter on a SPECT reconstructed image is illustrated in Figure 6. The filters plotted (upper right) were applied to the reconstruction of a central transverse slice from a 99mTc-HMPAO brain SPECT study. The resultant transverse slices are displayed along with a linear ramp reconstruction (i.e., no smoothing) for reference (bottom, far right). The best compromise between SNR and resolution provided by the Butterworth filter (Filter 3) is readily appreciated (see Fig. 6 caption). Again, the goal of filtering is to eliminate as much noise and retain as much signal as possible. The standard Hamming window is shaped such that, in order not to reduce the signal dominant at low frequencies, a substantial amount of noise above 0.5 Nyquist must be retained. However, to eliminate the noise dominant above 0.5 Nyquist with the Hamming window, the signal below 0.5 Nyquist also must be significantly reduced. Thus, neither of the 2 Hamming filters (Filter 1 and 2) are optimal. The Butterworth window, on the other hand, retains essentially all of the signal below 0.5 Nyquist while effectively eliminating all of the noise above 0.5 Nyquist. The unique feature of the Butterworth filter is the ability to change its shape through the order (i.e., as the order increases, the function has a steeper roll off around the cutoff frequency), allowing better adaptation of the filter function to the frequency characteristics of the projection data. For this reason, the Butterworth filter has become the most popular for SPECT imaging.
The effect of the choice of reconstruction filter on image noise/resolution. The 3 filters applied were (upper right): 1.0 Nyquist, 0.5 a Generalized Hamming (medium gray), 0.5 Nyquist, 0.5 a Generalized Hamming (light gray), and 0.5 Nyquist, 10th order Butterworth (dark gray). The corresponding reconstructions of a central slice from a 64 × 64 99mTc-HMPAO brain SPECT study (bottom, left to right) demonstrate the superiority of the Butterworth filter (much better resolution than the 0.5 Nyquist Hamming, yet both better resolution and less noise than the 1.0 Nyquist Hamming).
Three-Dimensional Filtering.
Originally, SPECT reconstruction and display were confined to transverse slices only, thus, the filtering was applied only along the horizontal dimension of the two-dimensional projection images (i.e., along the direction of the one-dimensional projection profiles of the two-dimensional transverse slices). This allowed for adjustment of the noise content and effective spatial resolution (i.e., smoothness or sharpness) of the reconstructed transverse slices, but no filtering between slices was performed. This led to distorted images when viewing any plane other than the transverse, such as coronal or sagittal. Figure 7 illustrates sagittal and coronal images generated with and without volume smoothing. With current state-of-the-art SPECT systems, slices both perpendicular to the transverse slices or in any other direction through the three-dimensional reconstructed volume also may be generated. Filtering is now routinely applied for filtered backprojection reconstruction in both dimensions of the two-dimensional projection images (so-called volume smoothing), which results in equivalent image SNR and spatial resolution in slices along any direction through the three-dimensional volume (and, hence, the term volume smoothing). However, with new iterative reconstruction programs, three-dimensional filtering may not be a part of the reconstruction as yet.
(A) Central sagittal and coronal slices without volume smoothing and (B) with volume smoothing, for a 128 × 128 99mTc-HMPAO brain SPECT study. A 0.3 Nyquist, 10th order Butterworth transverse reconstruction filter was applied to the transverse slices in A, and a 0.375 Nyquist, 10th order Butterworth volume smoothing filter was applied in B, such that the transverse slices had equivalent smoothness. Note the streaking between rows of pixels in A due to no filtering between transverse slices.
Other Types of Filtering.
Other types of reconstruction filters have been developed which attempt to optimize SPECT SNR and spatial resolution. They are the resolution recovery or Metz-Wiener filters (31,32). However, detailed measurement of the SPECT imaging system characteristics and careful analysis of the clinical scatter conditions are required for accurate filter design and in the filtered backprojection process, these corrections are difficult to implement. Therefore, such filters are currently not widely used with systems using solely filtered backprojection methods. Iterative reconstruction methods have advantages in this area and such corrections are more easily incorporated into the reconstruction algorithm.
Iterative Reconstruction Methods.
A major advancement in SPECT within the last 2–3 y has been the maturity of iterative reconstruction techniques. Holding promise for significant improvement in both reconstructed image quality and quantitative accuracy, iterative methods had languished in research labs for more than a decade. Most gamma camera vendors now offer at least 1 commercial version with their systems. The 2 primary reasons for this advent are: (a) iterative reconstruction became a requirement for accurate attenuation correction based on transmission source scan data; and (b) current state-of-the-art computer platforms have the central processing unit (CPU) speed required to perform these computationally intense reconstructions in a clinical time frame.
Iterative reconstruction algorithms involve an initial reconstruction of an object, inclusion of some additional information (e.g., a map of the attenuation of a patient's body superimposed on the radioisotope distribution) in a model of the object, forward calculation of projections from the (updated) model, and, finally, calculation of correction factors from the differences between the original and the model projections. The correction factors are used to update the model and make it more consistent with the projection data and the included information. This entire process can be repeated several times, thus the term iterative.
The primary advantage of iterative reconstruction over conventional filtered backprojection, is incorporation of the physics of gamma camera imaging into the reconstruction model. At the highest level, iterative reconstruction consists of essentially 2 steps. The first step involves calculating what is called a probability density matrix (PDMi) for each voxel Fi within the object distribution volume. Each data point Dij in the PDMi represents the probability (≥0) that the radioactivity at voxel Fi will be detected in pixel Pj in the projection set (or, equivalently, the probability that an event detected in pixel Pj originated at voxel Fi). Each Dij in each PDMi is typically calculated using both attenuation maps and/or resolution functions. The second step involves calculation of an initial estimate of the reconstructed slice (such as a traditional filtered backprojection), followed by repeated, or iterative, execution of the projection/backprojection process using the PDMs, until either a stopping criteria or a desired number of iterations has been reached (33).
The iterative projection/backprojection process is illustrated in Figure 8. The current estimate of the reconstructed slice, Fest, is projected using the PDM, creating an estimated projection set, Pest. The current Pest is then either subtracted from, or divided into, the original projection set, P, to form an error projection set, eproj. The original P may be smoothed, or regularized, first, to reduce the effect of Poisson statistical noise. The eproj is then backprojected, using an algebraic combination of the PDM and its transpose (rows and columns interchanged), producing an error reconstruction, errest. The errest is multiplied by a scale factor, r (between 0 and 1), to reduce oscillation in the iterative process, and is then either added to, or multiplied by, the current Fest, to produce a new Fest. The iteration cycle is then repeated from there.
Graphical representation of the iterative reconstruction process.
The first iterative techniques applied to SPECT were based on what is called the MLEM algorithm (maximum-likelihood expectation maximization). However, such an algorithm is extremely computer intensive, and requires many iterations to arrive at a good estimate. In recent years, an algorithm known as ordered-subset EM (OSEM), has emerged as an efficient alternative, by using only a subset of the entire projection set in each backprojection step (34). OSEM greatly reduces the number of iterations required, providing iterative reconstructions in a clinically acceptable timeframe (within several minutes or less for an entire SPECT volume). Thus, OSEM has become the current method of choice for commercial implementation.
Attenuation/Scatter and Correction
The counts in SPECT reconstructed images are, in theory, directly proportional to the absolute concentration of radiopharmaceutical in the organ or organ system of interest (e.g., mCi/cc or MBq/cc). The 2 main factors that currently prevent SPECT from achieving this quantitative goal are attenuation and Compton scatter of gamma rays during the imaging process. These 2 phenomena result in spatially dependent distortion of the measured activity concentration (35,36).
Attenuation.
For a concentration of radioactivity in the body emitting gamma rays, the relative number of gamma rays that escape the attenuating medium (i.e., the patient) and are detected by the gamma camera is determined by the equation:
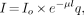 Eq. 4
where:
Eq. 4
where:
I = the attenuated intensity of gamma rays
Io is the gamma-ray emission intensity without attenuation
μ = the linear attenuation coefficient of the medium (for example, approximately 0.15 cm−1 for 99mTc in soft tissue)
lq = the depth of the medium between the source of activity and the gamma camera at projection angle q (Fig. 9).
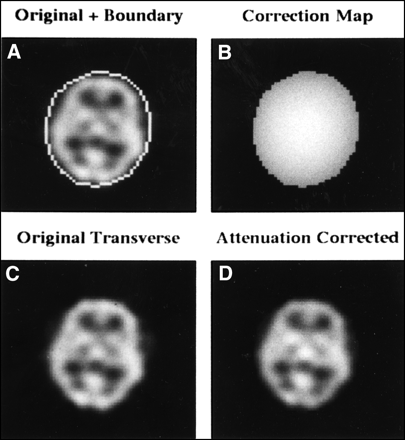
This results in the cupping artifact, where reconstructed activity in the transverse slice is reduced in an approximately exponential fashion from the edges of the patient toward the center. In SPECT studies in the brain or abdomen, which are dominated by soft tissue, μ is approximately constant. The attenuation phenomenon is much more complicated in the thorax, where μ varies throughout the volume (e.g., soft tissue, lungs, bone). Attenuation correction methods may be categorized as: (a) constant μ, or the Chang method; or (b) variable μ, or transmission source method (37–40). The most popular method of attenuation correction in the brain or abdomen, where the attenuating media can be considered essentially uniform, is the Chang method (37). An attenuation map, based on patient boundary determination and an approximate or measured, constant μ, is generated and applied to the reconstructed transverse slices (Fig. 10). Of course, this method will only work well when μ is, in fact, approximately constant. The newest method, and required when the attenuating media is nonuniform (cardiac studies), uses a variable attenuation coefficient dependent on the spatial location of the pixel in the patient. The quantitative value of μ is determined by the use of transmission scanning, either with moving line sources, or fixed sources of varying geometries. From the transmission scan, a μ map is generated, the inverse of which provides the attenuation correction factor. The transmission sources are usually long-lived isotopes of dissimilar energy to both 201Tl and 99mTc photons (usually 153Gd, with a nominal 100-keV photon), and therefore a correction factor must be applied to convert the attenuation coefficient of the transmission source energy to that of 201Tl or 99mTc.
The effect of attenuation on SPECT imaging. The intensity of photons emerging from a source of activity within an attenuating medium is reduced by exp (−μl), where μ is the linear attenuation coefficient (cm−1) and l is the depth of the activity in the attenuating medium at a particular projection angle. This produces attenuated projections (upper left) and the cupping artifact in the reconstructed transverse slices (lower right).
Chang postprocessing attenuation correction method. (A) Original uncorrected central transverse slice from a 128 × 128 99mTc-HMPAO brain SPECT study with a manually determined boundary of the head overlaid. (B) Correction map C (x,y) = M/S exp (−mlq), q = 1,2, . . ., M, where x,y is the pixel location within the boundary, M is the number of projection views, and lq is the depth of x,y within the boundary for projection angle q. (C) Uncorrected slice and (D) attenuation-corrected slice. Note the increase in activity toward the center of the brain. To avoid under- or overcorrection, the boundaries must be accurately defined (preferably in an automated fashion).
The accuracy of the transmission source attenuation correction methods depends on the strength of the transmission source, lack of patient motion, and the attenuation correction algorithm itself. As previously stated, variable μ attenuation correction may be best performed using iterative reconstruction methodology, although some have used filtered backprojection. The clinical accuracy of transmission scanning methods in perfusion SPECT imaging is currently the subject of controversy. Attenuation correction has been shown to be of some use (17), but complete correction in all patient studies still eludes the technology.
Compton Scatter.
The finite energy and spatial resolution of the SPECT imaging system allow the acceptance of a certain amount of Compton scatter gamma rays. The accepted scatter is dominated by narrow angle scattered gamma rays, which interact with orbital electrons and have an energy slightly less than that of pure photopeak gamma rays. Compton scatter degrades resolution and acts as a modifier to the effective attenuation coefficients in a depth dependent fashion. Moreover, misplaced Compton scattered events adversely effect image contrast. Some SPECT systems include scatter correction methods based on the physics and probability of the Compton scatter process and multiple or weighted energy windows (41). In addition, various approximate, postprocessing methods of correcting either projection views or transverse slices have been developed. In the future, improved energy resolution and window acquisition methods, and iterative reconstruction methods which include Compton scatter modeling, should provide further improvements in scatter removal (42).
Multimodality Fusion of Images
Different imaging modalities give different diagnostic information about a patient. CT images have excellent spatial resolution and anatomical detail. PET images show areas of metabolic activity as well as receptor sites. MRI images also have good spatial resolution and can be especially useful in diagnosing brain or central nervous system disorders. Because of the complementary information of these imaging modalities, several methods have been developed for the superposition of images from different modalities (43). These methods may be useful in pinpointing areas of the brain for surgical intervention. SPECT or PET images may locate the focus of an epileptic seizure, but, unless a neurosurgeon can find this focus surgically, perhaps not much can be done to help the patient.
The registration of these different modality images is not a simple problem. Consider that the different modalities have different size pixel dimensions, both in the transverse and axial dimensions, indicating that the slices must be geometrically transformed, or warped, to have the same pixel dimensions in the transverse plane. Then the number of slices will have to be interpolated to agree with the number of slices of the better spatial resolution imaging modality. After the three-dimensional warping of the respective imaging volumes, some method of correlating features of the studies must be developed.
Pelizzari et al. (44) have developed a method that finds the surface of the brain for each modality of interest, and then minimizes the overall distance or difference of these surfaces to match or overlay functional with anatomic information. This technique can be used for correlating function with different brain locations, finding sites for possible surgery, and for evaluating results of tumor therapy. Other applications also have been examined. They include the correlation of SPECT monoclonal antibody uptake with abdominal CT findings, correlation of SPECT with MRI, and correlation of MRI with ultrasound (US) and nuclear medicine for pediatric imaging (45).
Evaluation of SPECT Image Performance
As the nature of the SPECT image differs from planar imaging, it is important to understand how the unique aspects of the reconstruction process affect the interpretation of the scan. In planar nuclear medicine, the classic Poisson noise is the square root of the number of events. This would lead one to expect the noise is the square root of the total number of events acquired in the SPECT acquisition. However, in SPECT imaging, the noise present depends not only on the number of events counted, but also on the volume containing those events (image pixel size). The SPECT reconstruction process tends to propagate noise. As previously discussed, the expected signal to noise ratio is actually lower by a factor of over 10, particularly as voxel size decreases, as given by Equation 2. In a typical bone SPECT study, for example, there are about 20–25 million counts. If a 64 × 64 matrix is used, the percent rms noise is calculated by the above equation to be approximately 12%–13%. If other processes are applied to the SPECT reconstruction, such as attenuation correction or scatter correction, the noise may be further amplified. Noise tends to decrease lesion delectability, due to increased statistical uncertainty of the data, which hampers image interpretation by the physician. The effect of noise on contrast resolution is illustrated with the following. In medical imaging, it is contrast resolution that ultimately determines the ability of the observer to detect lesions. Lesion contrast is defined as:
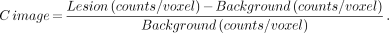 Eq. 5
According to Whitehead (11), there are 2 conditions for SPECT scanning which must be satisfied for lesion visualization. First, the magnitude of the lesion's image contrast must be greater than some factor, k, times the rms noise level or:
Eq. 5
According to Whitehead (11), there are 2 conditions for SPECT scanning which must be satisfied for lesion visualization. First, the magnitude of the lesion's image contrast must be greater than some factor, k, times the rms noise level or:
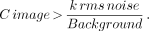 Eq. 6
The value of k is based on statistical criteria and balances the probability of false-positives and false-negatives. The value of k should be in the range of 4 to 5. Second, the observed lesion contrast must be greater than the visual threshold of the reader. In planar scanning, the major cause of loss of lesion contrast comes from the superposition of overlying and underlying tracer activity, which SPECT eliminates.
Eq. 6
The value of k is based on statistical criteria and balances the probability of false-positives and false-negatives. The value of k should be in the range of 4 to 5. Second, the observed lesion contrast must be greater than the visual threshold of the reader. In planar scanning, the major cause of loss of lesion contrast comes from the superposition of overlying and underlying tracer activity, which SPECT eliminates.
CONCLUSION
The improved contrast of SPECT scanning improves lesion detection as compared with planar imaging. The user can degrade image contrast in SPECT by the inappropriate choice of reconstruction filter and/or inadequate statistics in SPECT acquisition. A filter with too low a Nyquist frequency cutoff will eliminate spatial frequencies that contain image data and decrease the contrast of smaller lesions. Improved statistics during SPECT acquisition will allow higher cutoff filters to be used, but may not always be clinically practical. It can be appreciated that SPECT filter choice for optimum image contrast is a trade-off between reproducing important, detail containing, spatial frequencies, and minimizing noise.
Footnotes
For correspondence or reprints contact: Mark W. Groch, PhD, Department of Nuclear Medicine, Northwestern Memorial Hospital, 251 E. Huron St., Chicago, IL 60611; Phone: 312-926-2514.