Abstract
Molecular imaging technologists face statistics every day because they perform diagnostic imaging on patients who have been selected on the basis of how well the imaging test performs and because that performance can be influenced by a variety of technical factors. Choosing the test for a patient requires an understanding of the patient’s pretest likelihood of disease, the performance of the test, and other clinical factors that may affect the results. Terms such as sensitivity, specificity, accuracy, and predictive value are used to describe how a diagnostic test performs or how it compares with other diagnostic tests. Although nuclear medicine and PET technologists study these concepts in training programs, applying this learning to daily patient care can be daunting given that new tracers and technologies are continuously entering clinical practice. Advances in research continue to challenge diagnostic paradigms with new patient populations, increasingly sophisticated technology, and the advent of large databases with which to study population outcomes. This article—part 1 of a 2-part series—is a refresher on the basic clinical statistics that are useful in understanding how diagnostic testing is optimally applied in patient care.
Among those who work in a diagnostic testing arena, the concept of “testing the test” is familiar. We observe in our patients, and in our personal health, that not every test is perfect. We ask ourselves how an 18F-FDG PET scan missed cancer that was subsequently found at surgery, or how a patient with positive myocardial perfusion results had negative cardiac catheterization results. We hear that one test is more sensitive or specific than another. What exactly does that mean? The answer lies in the fact that no test is 100% sensitive and specific, and the characteristics of all diagnostic tests must be evaluated for usefulness in certain diseases or conditions.
The purpose of this article, part 1 of a continuing education series, is to provide a fundamental review of basic concepts in diagnostic testing such as sensitivity, specificity, negative and positive predictive value, and pretest and posttest likelihood to help molecular imaging technologists understand how diagnostic tests are evaluated and how test performance informs medical decision making. Part 2 of the series will discuss significance, standard deviation, and confidence levels to aid technologists in being increasingly discerning consumers of statistics in medical research. In both parts, examples from the clinical literature are used to highlight specific statistical concepts. However, mention of a published statistic about any product or procedure should not be misconstrued as a substitute for thorough clinical and scientific discussion. Instead, it is hoped that statistical concepts will more easily come to life when placed in the context of real-world molecular imaging.
SENSITIVITY AND SPECIFICITY
One of the first questions that could be asked about a diagnostic test is how sensitive and specific it is. Sensitivity is a performance characteristic of a diagnostic test that describes how well the test can detect a disease given that the disease is present. A diagnostic test that is 100% sensitive has 100% probability of finding disease when an agreed-on standard measurement (truth standard) says there is disease. A 50% sensitivity indicates a 50% likelihood that the disease will be found if the patient truly has the disease—essentially a flip of a coin.
Specificity, on the other hand, is the ability to rule out disease in truly disease-negative patients. A test that is 100% specific means that when no disease is present, the test has a 100% probability of showing negative results (normal). A 50% specificity means that there is a 50% chance of a positive test result when the patient does not have the disease.
COMPARISON TO STANDARDS
Choosing the standard on which sensitivity or specificity calculation is based is essential. To measure the performance of any diagnostic test, there must be a separate disease-assessment method that is considered “truth.” Sometimes imaging tests are evaluated by comparison to a reference standard: either an imaging test or clinical diagnosis. Such comparisons can be valuable but may not give a true estimate of sensitivity and specificity because the standard may have significant limitations. Ideally, a truth standard will be a “gold standard,” an actual assessment of the physiologic or pathologic condition the scan is evaluating. For example, in assessing the performance of nuclear cardiology techniques, cardiac catheterization is typically considered the gold standard to which SPECT and PET myocardial perfusion procedures are compared. If a group of patients undergoes a PET myocardial perfusion scan followed by cardiac catheterization, comparison of the results of the two techniques allows the sensitivity and specificity of the PET scan to be calculated. If PET imaging were positive every time catheterization is positive, the sensitivity of PET imaging would be 100%, meaning that all abnormal PET findings are true-positives (TPs). Conversely, if PET imaging were negative every time catheterization is positive, the sensitivity of PET imaging would be 0%, meaning that the negative findings on PET imaging are false-negatives (FNs). Specificity would be measured by how often the negative results concur between the two techniques. If PET imaging were negative every time catheterization is negative, specificity would be calculated at 100%, indicating true-negatives (TNs). If PET imaging were to show abnormalities when the catheterization is negative, the specificity percentage would drop because of false-positive (FP) findings (1).
Standard of Truth
An ideal gold standard for evaluation of diagnostic test performance would compare identical physical and biologic processes between the diagnostic test and the gold standard. Perfect gold standards are hard to come by, however, and rarely does another imaging standard completely mirror a biologic process identical to that mirrored by the diagnostic test. For example, using cardiac catheterization as a gold standard for perfusion imaging can be problematic because the two tests demonstrate different processes. Cardiac catheterization demonstrates macroscopic blockage in an artery, whereas perfusion imaging demonstrates the downstream impact of blocked arteries by showing perfusion (or lack thereof) into myocardial tissue at a microvascular level. A small lesion that is visible on a perfusion image may be the result of an artery that is less than 70% blocked. Because the positive threshold for catheterization is 70% or higher, the catheterization result, in this case, would be considered negative although the perfusion image is positive. This type of mismatch leads to inaccurate descriptors of test sensitivity and specificity in patients showing mild disease on perfusion imaging.
Sometimes the standard to which imaging procedures are compared is not another imaging test but pathologic tissue confirmation from biopsy or autopsy sampling. Most molecular imaging techniques in oncology, for example, are subject to comparison to a standard of truth such as microscopic confirmation of histopathology. Patients commonly undergo biopsy confirmation for cancers before treatment is prescribed. Thus, the comparison of imaging findings to pathologic findings is reasonable within the boundaries of patient care. However, there are some diseases (such as certain brain diseases) for which obtaining the standard of truth is not possible while the patient is alive. In such cases, diagnostic sensitivity and specificity can be measured only by comparison with the best available diagnostic test, which is then referred to as the reference standard. An example of this is Lewy body dementia, for which the standard of truth is pathologic evidence of Lewy bodies (a toxic protein) in the brain at autopsy. Currently, the gold standard for imaging of Lewy body dementia is SPECT with 123I-ioflupane (DaTscan; GE Healthcare), which characterizes the impact of the disease on dopamine receptors (2).
Sensitivity and Specificity of Screening Tests
Most molecular imaging techniques are not used for screening because of their cost, complexity, or less than 100% sensitivity. Tests that are used to screen a population for disease must be very sensitive and relatively inexpensive in order to detect abnormalities over a large population without putting undue financial stress on the health-care system. An example of a commonly used method of screening is blood pressure measurement to screen for primary hypertension, a test that can be performed quickly in many health-care settings for a wide range of patients and minimal cost. Blood pressure testing at routine ambulatory-care clinical visits has been shown to be 100% sensitive in detecting hypertension (3). With blood pressure testing having a specificity of 70%, detection of an elevated blood pressure during a clinical visit for a truly normotensive patient could be a FP result in 30 of 100 cases because of conditions other than primary hypertension, such as anxiety or pain. In these cases, further testing or repeated testing is required to rule out the possibility that the abnormal reading is due to some cause other than true hypertension.
Alternatively, if the test is highly specific, its results, if negative, can be counted on to be a true reflection of the absence of disease. For example, oncologists rely on 18F-FDG PET to rule out malignancy in indeterminate solitary pulmonary nodules (larger than 1 cm) because the test has been shown to have a high TN rate for that lesion type and size. If the lesion is not 18F-FDG–avid, there is high confidence that it is not malignant (4).
Sensitivity and Specificity Trade-off
Because patients often have different biologic and physiologic responses to disease processes, and because no diagnostic test is 100% correct in all cases, there is typically a trade-off between sensitivity and specificity—an increase in sensitivity that comes with a loss of specificity and vice versa. This trade-off can be modified and minimized with technique (e.g., increasing sensitivity by reducing slice thickness in an MRI or CT scan) or with interpretation guidelines (e.g., increasing specificity by using lesion-size thresholds for positivity). Even given such modifications, however, it is highly unlikely that any diagnostic test would be able to routinely provide 100% specificity and 100% sensitivity when performed over many cases.
Sensitivity and Specificity Formulas
Sensitivity
The measurement of sensitivity is mathematically described as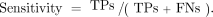
In other words, when disease is truly present one can describe how well a diagnostic imaging test determines that by dividing the TPs on imaging by the positives on the gold standard (TPs on imaging + FNs on imaging). Sensitivity relies on the presence of disease and is not affected by disease prevalence. This means that regardless of whether the expected number of patients with a disease is 1 of 100 or 1 of 1,000, the sensitivity of the test remains the same.
Specificity
Specificity, on the other hand, reflects how well a diagnostic imaging test rules out disease; that is, the imaging results are negative when disease is not present. Specificity is conditional on the absence of disease and, like sensitivity, is not affected by disease prevalence. The formula for specificity is
In other words, when disease is truly absent one can describe how well a diagnostic imaging test determines that by dividing the TNs on imaging by the negatives on the gold standard (TNs on imaging + FPs on imaging). If a study includes only patients with disease, however, it is not possible to determine specificity because the measurement requires TNs. This is often a limiting factor in institution-based clinical research, as applying the test to subjects who do not have the disease is not always feasible or ethical, depending on the level of risk to the subject. For example, many patients with negative myocardial perfusion results do not go on to cardiac catheterization.
2 × 2 Contingency Tables for Calculations
A simple 2 × 2 table (Fig. 1) can be used to visually display the results of comparison with a gold standard and easily calculate the sensitivity and specificity of a test. For consistency, it is recommended that the true diagnosis (gold standard or standard-of-truth results) be at the top and the diagnostic test results at the side as seen in Figure 1.
2 × 2 contingency table used to visually display test results vs. gold standard.
Here is an example of how a new molecular imaging agent was evaluated regarding sensitivity and specificity. In a recent publication by Bach-Gansmo et al. (5), the characteristics of a new tracer, 18F-fluciclovine (Axumin; Blue Earth Diagnostics), for recurrent prostate cancer were reported. The authors looked at patients with previously treated prostate cancer who now presented with rising levels of prostate-specific antigen. Historically, pelvic CT, MRI, and bone scanning have had limited sensitivity in detecting disease in this population. (Choueire et al., in 2008, reported a 40% positive rate for MRI and a 10% positive rate for bone scanning and CT (6).) To demonstrate the effectiveness of the new molecular imaging tracer, researchers compared the imaging results against the histopathologic biopsy results as the standard of truth. How were sensitivity and specificity calculated? Here are the raw data that were presented to the study statisticians: 553 lesions were biopsied, 244 were pathologically positive, 309 were pathologically negative, 153 were positive both pathologically and on imaging (TPs), 93 were pathologically negative but positive on imaging (FPs), 216 were negative both pathologically and on imaging (TNs), and 91 were pathologically positive but negative on imaging (FNs). By entering these data into the table (Fig. 2), it is possible to describe the performance of 18F-fluciclovine PET on a per-lesion basis:

Sample data for sensitivity and specificity calculation.
In this example, the test showed higher sensitivity and specificity for PET with the new tracer than for previously available techniques. Importantly, the testing was performed on a population in whom disease was suspected but not confirmed—in other words, patients with a moderate pretest likelihood of disease. Pretest likelihood is an important consideration when evaluating the performance of a diagnostic test.
PRETEST LIKELIHOOD
Pretest likelihood is an estimate of how probable it is that the patient has disease before the diagnostic test results are known. Information from the physical examination, history, risk factors, or other tests is factored into estimations of disease likelihood. Diagnostic testing is most useful when there is a moderate pretest likelihood and when the results have the highest potential to alter the clinician’s assessment of disease likelihood. The most substantial shift from pretest to posttest likelihood is demonstrated in patients for whom presence of the disease is possible but not confirmed. Bayes theorem is a mathematic formula that enables prior knowledge about the probability of a diagnosis (pretest likelihood) to be combined with test results to obtain a posttest assessment of probability (posttest likelihood). Figure 3 illustrates Bayes theorem in a hypothetical population of patients with 3 tests of varying accuracy.
(A) Graph of pretest and posttest likelihood of disease. Accuracy of 3 diagnostic tests is displayed: 95%, 70%, and 50%. Upper 95% and 70% lines are used to determine posttest likelihood of disease when scan result is positive. Lower 95% and 70% lines are used to determine posttest probability when test is negative. (B) To demonstrate, a patient who has 1% pretest likelihood is not likely to shift into high posttest likelihood regardless of whether test is positive or negative and regardless of measured accuracy of test (blue arrow). Conversely, patient who has 99% pretest likelihood and negative test result still has high posttest likelihood of disease (green arrow). To demonstrate further, if patient has 90% pretest probability of disease and positive result on test that is 70% accurate, posttest likelihood of disease is 93% (dotted-dashed line). Most dramatic change between pre- and posttest likelihood occurs in moderate-likelihood population of 40%–60%. Patient with pretest likelihood of 50% who has negative result on test that is 70% accurate shifts to posttest likelihood of 30% (lower dashed line). If result is positive, posttest likelihood is 70% (upper dashed line). Improved accuracy of test shifts curve even further: 50% pretest likelihood with negative result on test that is 95% accurate produces posttest likelihood of 5% (lower dotted line), whereas positive result produces posttest likelihood of 95% (upper dotted line). Regardless of scan result and pretest likelihood of patient, test that is only 50% accurate does not allow shift in pretest likelihood.
ACCURACY
The formula for accuracy includes variables previously discussed for sensitivity and specificity (TNs and TPs) and again is not affected by the disease prevalence in the population. The formula for accuracy is
If we refer to the example of 18F-fluciclovine, we can use this formula to determine the accuracy of the scan:
Applying this accuracy level of roughly 70% to the graph in Figure 3, we can estimate that a 50% pretest likelihood of recurrent metastases (based on history, prostate-specific antigen level, physical signs and symptoms, and other diagnostic testing) will drop to 30% if the 18F-fluciclovine PET result is negative but will rise to approximately 75% if the result is positive. Hence, the diagnostic test performs well in terms of shifting the clinician’s estimate of disease likelihood.
POSITIVE AND NEGATIVE PREDICTIVE VALUE
Sensitivity, specificity, and accuracy are calculations based on tests in a sample population. Calculations of positive and negative predictive value (or probability) use the estimated accuracy of the test and factor in disease prevalence. Therefore, unlike sensitivity, specificity, and accuracy, the positive and negative predictive value of a diagnostic test is highly influenced by the prevalence of disease in the sample population:

Borrowing from a previously published teaching example by Koller (1), assume you are trying to determine the positive and negative predictive value of myocardial perfusion imaging in 1,000 young, asymptomatic subjects in whom disease prevalence is estimated to be 5%, and the test is known to perform at 90% sensitivity and 80% specificity. A disease prevalence of 5% means that of 1,000 patients, 50 will have the disease (TPs) and 950 will not (TNs). In this type of analysis, the disease prevalence takes the same location as a gold standard in the 2 × 2 contingency table, as seen in Figure 4. For a test that performs at 90% sensitivity, the number of TPs will be 90% of 50 patients, or 45. With an 80% specificity, of the 950 patients who are expected to be normal, 80%, or 760, will be TNs:

Sample data for positive and negative predictive value calculation.
Therefore, in this example of a sample population with a low disease prevalence and a diagnostic test with 90% sensitivity and 80% specificity, a negative scan has a strong ability to predict that the patient does not have disease (99% likelihood). However, a positive scan provides only a 33% probability that the patient has disease.
In contrast, assume that a patient is middle-aged and has typical chest pain and the disease prevalence is 90%. In a cohort of 1,000 patients with typical chest pain, 900 are assumed to have disease and only 100 would be expected to be free of disease. Applying the same formulas, and assuming the same sensitivity and specificity of testing, the 2 × 2 table would look like this (Fig. 5):
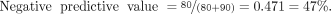
Second set of sample data for positive and negative predictive value calculation.
These two examples illustrate the importance of disease prevalence when calculating the probability of disease presence or disease absence. The consumer of imaging statistics must be knowledgeable and ask appropriate questions when presented with probability statistics about a diagnostic test.
PRACTICAL IMPLICATIONS
At the PET center level, technical factors can play a significant role in optimizing or reducing the sensitivity, specificity, and accuracy of any molecular imaging test. The use of 18F-FDG PET in head and neck cancer is an excellent example. PET has been found to be 79.9% sensitive and 87.5% specific for the detection of residual head and neck cancer after primary therapy with chemotherapy and radiation, with a negative predictive value of 94.5%. In this instance, molecular imaging outperforms conventional imaging in terms of sensitivity, specificity, and negative predictive value (7). However, these excellent results are not reproducible for all patients if technical factors are not controlled. If the patient is not properly prepared, has eaten, has an elevated glucose level, or has had an insufficient uptake time, the scan may have reduced sensitivity (disease missed because of altered biodistribution or inadequate clearance from background) or reduced specificity (FP areas due to muscle or brown fat). Motion during acquisition can skew sensitivity or specificity by blurring the images. Technologists can have a direct impact on test performance by consistently following best practices for the modality regarding patient preparation, injection conditions, uptake time, and motion prevention.
CONCLUSION
This article has discussed key statistical concepts frequently used to describe diagnostic imaging examinations. Sensitivity, specificity, accuracy, and predictive value explain how well a test performs and are routinely used to compare one diagnostic test with others. The goal of this article was to provide a refresher on the basic performance statistics routinely used in clinical decision making and to identify the critical role technologists play in maximizing these statistics by providing the high-quality diagnostic studies needed to do so. Part 2 of this series, which will appear in a future issue of this journal, will continue to review statistical concepts, with a focus on variability. Interreader and intrareader reliability, statistical significance, standard deviation, and confidence levels will be discussed.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Acknowledgments
I thank LisaAnn Trembath, CNMT, MSM, CCRA, FSNMMI-TS. Without her brilliance and support, this article would not have been possible.
Footnotes
Published online Dec. 22, 2017.
CE credit: For CE credit, you can access the test for this article, as well as additional JNMT CE tests, online at https://www.snmmilearningcenter.org. Complete the test online no later than March 2021. Your online test will be scored immediately. You may make 3 attempts to pass the test and must answer 80% of the questions correctly to receive 1.0 CEH (Continuing Education Hour) credit. SNMMI members will have their CEH credit added to their VOICE transcript automatically; nonmembers will be able to print out a CE certificate upon successfully completing the test. The online test is free to SNMMI members; nonmembers must pay $15.00 by credit card when logging onto the website to take the test.
REFERENCES
- Received for publication October 23, 2017.
- Accepted for publication December 14, 2017.












