Abstract
The purpose of this study was to develop spreadsheet workbooks that assist in the radiation safety counseling of 131I therapy patients and their families, providing individualized guidelines that avoid imposing overly conservative restrictions on family members and others. Methods: The mathematic model included biphasic patient radionuclide retention. The extrathyroidal component was a cylindric volume with a diameter corresponding to the patient’s size and included patient self-absorption, whereas the thyroidal component was a point source whose transmission was reduced by self-absorption. A separate model in which the thyroid, extrathyroid, and bladder compartments fed serially from one to the next was developed to depict the radionuclide levels within the patient and to estimate the activity entering the environment at each urination. Results: The system was organized into a set of 4 workbooks: the first to be used with ablation patients prepared using thyrogen, the second with ablation patients prepared by deprivation, the third with hyperthyroid patients, and the fourth with the unusual hyperthyroid patient who finds the restrictions to be oppressive and returns 5–10 d after administration for a measurement and reassessment. The workbooks evaluated the radiation field strength external to the patient and indicated restrictions based on selected dose limits. To assist physicians in suggesting contamination precautions, the workbooks also evaluated the radioactivity present within the patient and the estimated discharge into the environment as a function of time. Conclusion: The workbooks that were developed assist the radiation safety counselor in individualizing radiation protection procedures for the family of patients undergoing 131I therapy. The workbook system avoids overly conservative assumptions while permitting selection of appropriate dose limits for each individual.
Facilities that offer 131I therapy must counsel the patients who receive it, and their families, about radiation safety. Published guidelines to facilitate this process are necessarily generic. The guideline provided by the American Thyroid Association, for example, assumes that the thyroid remnant of an ablation patient has an 131I uptake of 2% and that the intact thyroid of a hyperthyroid patient has an uptake of 50% (1). To avoid imposing excessive restrictions on a large number of families, these are reasonable assumptions. However, if a surgeon were to report an unusually large thyroid remnant, the 2% assumption may not be appropriate. Also, it is not unusual to encounter a hyperthyroid patient whose uptake significantly exceeds 50%. These less common situations require more severe restrictions, but they should be no more oppressive than necessary.
Development of an Excel (Microsoft) spreadsheet that generates customized restrictions for patients and families has been previously reported (2). When the user enters a few parameters, individual restrictions are automatically computed for adult family members, the sleeping partner, held children, and coworkers. Use of such a spreadsheet transforms individualized dose computations from a dreaded process into a trivial one, and a printout of the sheet can be filed as documentation of counseling for review by regulators during inspections. In the work presented below, this spreadsheet has been expanded. By modeling the patient’s extrathyroidal compartment as a volume source, the spreadsheet can realistically follow, over the course of therapy, the influence of this volume source on the radiation field strength external to the patient versus that of the thyroid point source. A separate model was developed to estimate radionuclide activity that remains in the extrathyroidal compartment as a function of time, as well as the activity released at each urination. Finally, worksheets were added to permit reassessment, a few days after administration, of particularly oppressive restrictions on a patient’s activities and then to develop a strategy to resolve the conflict between patient needs and acceptable dose limits to family members.
These worksheets are partitioned into 4 Excel workbooks. Workbook 1, Ablation—Thyrogen Preparation, is intended for use with 131I ablation patients when the patient’s overall thyroid-stimulating hormone level has been enhanced by administration of exogenous human thyroid-stimulating hormone (Thyrogen). The therapeutic goal for these postthyroidectomy patients is to destroy the thyroid remnant and potential metastatic disease. Workbook 2, Ablation—Prepared by Deprivation, is for use when the ablation patient’s thyroid-stimulating hormone has been enhanced by thyroid hormone withdrawal. Workbook 3, Hyperthyroid—Initial Calculations, is for use, initially, with all hyperthyroid patients. Workbook 4, Hyperthyroid—Reassessment by Measurement, is for use in the unusual situation that a hyperthyroid patient finds the restrictions of workbook 3 to be oppressive and returns 5–10 d after 131I administration to have the strength of the radiation field measured so that restrictions may be reassessed and a strategy developed to satisfy patient needs while providing adequate radiation protection to children in the family.
MATERIALS AND METHODS
Two simple models were used to provide estimates of 131I behavior in the therapy patient. A geometric representation of the first, called the parallel model, is given in Figure 1. There are 2 compartments, corresponding to the extrathyroidal space and the thyroid. Because the number of compartments is 2, a biphasic retention curve is produced, as illustrated in Figure 2. The parallel model does not provide a realistic representation of the isotope’s flow pattern within the patient; its purpose is to create only a biphasic retention curve that, for a critical few days after administration, is found to satisfactorily represent the temporal behavior of the external radiation field strength about the patient.
Geometric representation of parallel model. Fraction of administered radionuclide that initially resides in extrathyroidal space and remaining fraction taken up by thyroid are represented by F1 and F2, respectively. Radionuclide in each of these compartments biologically transfers directly into excretion compartment with rate constants λbio1 and λbio2. Although this flow pattern is biologically unrealistic, it provides typical biphasic retention profile, and it has advantage of being mathematically simple. Radionuclide content of extrathyroidal space, modeled as uniformly distributed cylindric volume source, and content of thyroid, modeled as point source, determine radiation field strength in vicinity of patient.
Biphasic retention function generated by parallel model using parameters that would be suitable for thyrogen-prepared 131I ablation patient. For phase 1 (extrathyroidal space), initial uptake is 97% and effective half-life is 8 h. For phase 2 (thyroid), initial uptake is 3% and effective half-life is 5 d.
To provide a somewhat more realistic representation of the isotope’s flow pattern within the patient, the second model, the serial model, was introduced, as illustrated in Figure 3. Here, rather than the thyroidal compartment excreting the isotope directly, as depicted in the parallel model, the isotope migrates into the extrathyroidal space and from there into the urinary bladder. The advantage of the parallel model is that mathematically it is much simpler than the serial model, yet it satisfactorily represents the temporal behavior of the external radiation field about the patient, whereas the serial model is a more realistic depiction of the isotope’s migration within the patient. Table 1 provides a key to the notations used during the mathematic developments of the 2 models that follow.
Geometric representation of serial model. Radionuclide in compartment 2 (thyroid) biologically transfers into compartment 1 (extrathyroidal space) and that in compartment 1 transfers to bladder, which then periodically empties into environment. This model is used to estimate radioactive content of each compartment and of periodic urinations as function of time.
Mathematic Notations and Definitions
Parallel Model
For the parallel model, Figure 1, the basic mathematics for both compartments are identical, although the values of the constants F and λbio differ. For each of the 2 compartments, there is no entrance pathway for the isotope and there are 2 exit pathways, by transition to the excretion compartment and by radioactive decay. The differential equation for the ith compartment is then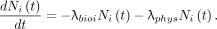
With the initial condition, 
, the solution to this equation is
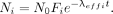The total isotope retention as a function of time (Fig. 2) is then
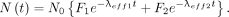The air kerma rate from the patient is the product of 4 factors: the activity of the radionuclide (given by the equation above), its air kerma rate constant, the fraction of radioactive emissions that is not absorbed within the patient, and a distance factor that is dependent on the geometry of the radiation source and the distance from the patient to the dose point. Therefore, the air kerma rate (mGy/h) from the thyroid, modeled as a point source, is
To simulate the extrathyroidal volume source, it was modeled as a cylinder of water within which were placed 37 line sources parallel with the cylinder’s axis. Each line source had an initial activity 1/37th of that taken up by the extrathyroidal compartment, and the activity was uniformly distributed along the source. To provide a uniform distribution of sources throughout the cylinder, each source was centered within contiguous areas, each area equal to 1/37th of the cylinder’s cross-section. The composite radiation field strength external to the cylinder including self-absorption for each line source was computed as
where gi is the perpendicular distance from the ith line source to the dose point, Δgi is the perpendicular distance from the ith line source in the direction of the dose point to the intersection with the cylinder wall, and when Δgi is multiplied by the ratio 
the product is the diagonal distance between the line source element, dl, and the dose-point ray’s intersection with the cylinder’s wall. The numerator of the integrand is then the cylinder’s transmission of radiation from this line source element. The integration for each of the 37 line sources was performed numerically using Excel. The composite air kerma rate (mGy/d) at the dose point, that is, at the position of the bystander, is
where 24 is the conversion, h/d. Recognizing that air kerma is air kerma rate times time, from the previous 3 equations the total air kerma due to emissions of the radioisotope retained by the patient that is received by a bystander who is present a fraction Toc of the time after a start time ts is
When the substitution 
is made and the integration with respect to time completed, this total air kerma (mGy) becomes
Eq. 1where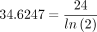 
. The transmission of radiation from the thyroid, B2, is simply
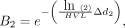where Δd2 is the water equivalent thickness of tissue that the 364-keV photon is assumed to traverse as it escapes from the thyroid (the estimate Δd2 = 1.5 cm, that is, 0.015 m, was used).
To investigate the effect of patient size on the radiation field strength, the air kerma to bystanders was computed using for the extrathyroidal source a variety of cylinder diameters. As the cylinder size changed, the 37 line sources redistributed automatically to maintain a uniform dispersal of sources throughout the entire volume. As expected, the radiation field strength exposing a bystander decreased as the size of the patient increased, partly due to increasing the volume through which the source was distributed but primarily due to an increase in self-absorption. During this investigation, it was a fortuitous discovery that, by replacing the 37 line sources with a single line source of their combined activity, the computed radiation field strength external to the patient from this single source could duplicate that of the 37 sources to within a couple percent over the distance range from the patient of 0.1–3 m. Geometrically, this single line source is parallel to the cylinder’s axis, it is in the plane determined by this axis and the dose point, and it is the length of the cylinder. For the resulting computed external field strength to replicate truthfully that of the distributed 37 sources, the single line source must be at a specific depth that depends on the cylinder’s diameter. The computed self-absorption of the single line source at this specific depth differs somewhat from that of the cylinder with the 37 line sources; however, this is irrelevant in the sense that the external field strength is nevertheless truthful. Thus, Equation 1 is replaced with
Eq. 2where in the integrand Δd1 is the specific depth of the single line source corresponding to the selected cylinder (patient) diameter, and d1 + Δd1 is the total distance from the line source to the dose point, that is, the bystander. The first term in the curly brackets represents the extrathyroidal (cylindric source) component and the second term the thyroidal (point source) component of the computation. Equation 2 is used to compute all doses to bystanders from patient emissions provided by the workbooks.
Serial Model
The thyroid compartment (compartment 2), as for the parallel model, has no entrance pathway for the isotope and 2 exit pathways, by radioactive decay and by transition to the extrathyroidal compartment (Fig. 3). The differential equation is then
and with the initial condition that 
, the solution is
Eq. 3Equation 3 is the basis for the patient’s thyroid activities computed by the serial model.
The extrathyroidal space (compartment 1) has 1 entrance pathway, by transition from the thyroid (compartment 2), and 2 exit pathways, by radioactive decay and by transition to the excretion/secretion compartment (represented as bladder in Fig. 3). The differential equation is then
where 
is given in Equation 3. With the initial condition, 
, as shown by Steward (PG Steward, unpublished document, 8/25/16, available upon request) the solution is
Eq. 4Equation 4 is the basis for the patient’s extrathyroidal space activities computed by the serial model.
The excretion/secretion compartment (compartment 3) has 1 entrance pathway, by transition from the extrathyroidal space (compartment 1), and 1 exit pathway, by radioactive decay (Fig. 3). The differential equation is then
where 
is given in Equation 4. With the initial condition that at some arbitrary time t = T, 
, as shown by Steward (PG Steward, unpublished document, 8/25/16, available upon request), the solution is
Eq. 5With the approximation that all excretions accumulate as urine in the bladder, Equation 5 provides the isotope’s activity to be urinated at time t, if the previous urination had occurred at time T. Letting T = 0 and recognizing that F1 + F2 = 1, Equation 5 becomes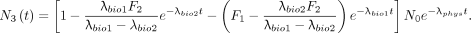
Eq. 6Equation 6 provides the total isotope activity excreted since administration that has not yet decayed.
RESULTS
The first 3 workbooks each have 2 worksheets, labeled EXT and INT. The EXT sheet evaluates the radiation field strength external to the patient using Equation 2 (parallel model). The upper section of this sheet that contains the cells used to input values needed for Equation 2 is shown in Figure 4. Values for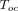 
(cells J5 through J8), N0 (cell O2), d1 (G5 through G8), d2 (H5 through H8), Δd2 (O5), 
and 
(N8 and O8), and F1 and F2 (N7 and O7) are input, and resulting air kerma and assumed equivalent to effective dose then appear in rows 15 and below (Table 1 provides symbol definitions). Δd1, the depth of the extrathyroidal line source in cell N5, is not input (no yellow fill), because this parameter is computed based on the patient diameter entered by the user in H2. As an example of the flexibility afforded by the workbooks, in cell G8 notice that for the thyroidal point source the patient–to–held child distance is 30 cm (0.3 m), but in cell H8, that for the extrathyroidal line source this distance is input as only 10 cm (0.1 m). The rationale for this apparent discrepancy is that the infant, being bottle-fed by the patient, is in direct contact with the patient’s abdomen/thorax, but at a greater distance from the thyroid remnant.
Small section of EXT worksheet of workbook 2. Cells that are unprotected and thus available to user for input have yellow fill. Cells corresponding to forbidden doses have magenta fill, and those with permitted doses are green.
The INT sheet, not shown, evaluates and displays, as a function of time, the radionuclide activities in the patient’s thyroid, extrathyroidal space, and bladder using Equations 3 through 6 (serial model). It also estimates the amount of radionuclide discharged at each urination. This information may have application when the risk of contamination or nuclide transfer, for example, to an infant, may be a concern.
The 2 workbooks for ablation patients (for patients prepared by thyrogen vs. by hormone deprivation) are separated to call attention to the fact that kidney function is known to be profoundly influenced by thyroid status (3). Because removal of 131I by the kidneys from the extrathyroidal compartment is substantially delayed for hypothyroid patients, the default value of 
for patients prepared by deprivation is 16 h, whereas that for those prepared using thyrogen, who are assumed to be euthyroid, is 8 h. Another observation of interest in this context is that there is indication that the thyroid of patients prepared by thyrogen administration may retain the iodine somewhat longer than those prepared by deprivation (4).
One anticipates that the uptake values, F1 and F2, and the nuclear decay, λphys, should be identical in the parallel and serial models; however, because of the obvious kinetic differences between the 2 models as depicted in Figures 1 and 3, values of the biologic rate constants, λbio1 and λbio2, for the serial model are expected to differ somewhat from the values used in the parallel model. Because we set these rate constants of the parallel model to simulate what we expect to be the true temporal behavior of the radiation field strength external to the patient, we use this temporal behavior to determine the biologic rate constants for the serial model. Specifically, we first generate the biphasic time profile (Fig. 2) of the isotope retention using each model. Then, in iterative fashion using the least-square minimization technique, the serial model’s λbio1 and λbio2 are determined so that the biphasic time profiles of the 2 models match. A detailed description of this process is available (PG Steward, unpublished user's manual, 3/11/17).
The third of the 4 workbooks, Hyperthyroid—Initial Calculations, consists of an EXT and INT sheet, as described above. The intact thyroids of these patients often have unusually high iodine uptake. As a consequence, even though relatively low activities of 131I are administered to these patients, external radiation field strengths can be high enough and persistent enough to require severe restrictions regarding the patient’s associations with children in the family, depending on the dose constraint that is used for children. For these patients, a recent thyroid radioiodine uptake study is recommended (5), but even if a thyroid uptake study is available, there are uncertainties regarding the value of λbio2, that is, the rate that 131I leaves the thyroid by biologic transition. In a group of 127 hyperthyroid patients, both the thyroid’s biologic half-life for radioiodine release and the uptake of radioiodine were studied (6). With the biologic half-life plotted against the uptake fraction, there appears to be an inverse relationship between uptake and half-life, but the data are so scattered (the biologic half-life varies from nearly zero to about 75 d) that no specific half-life can be reasonably associated with an uptake value. A straight line was drawn through the data that placed approximately 90% of the half-lives below and 10% above the line. In the EXT sheet of workbook 3, this line and the measured uptake value are used to determine the biologic half-life, 
, for release of iodine from the thyroid of a hyperthyroid therapy patient. Thus, we anticipate that restrictions based on this workbook that are placed on a hyperthyroid therapy patient’s interaction with children will be overly restrictive 90% of the time.
As indicated above, the large uncertainty in the half-life for the release of iodine from the thyroid of hyperthyroid patients compels, for safety reasons, a conservative estimate of this parameter used in workbook 3. Nevertheless, most patients comfortably comply with the resulting restrictions. However, sometimes, for example when the patient is the mother of an infant, the restrictions are perceived as oppressive. This prompted development of workbook 4 (Hyperthyroid—Reassessment by Measurement). When this workbook is used, the patient returns for reassessment 5–10 d after administration, the time to be selected when it is believed that the 131I pool in the extrathyroidal space is sufficiently depleted that essentially all residual 131I activity is localized in the thyroid (the INT worksheet may assist here). The EXT sheet of this fourth workbook has been extended to include the following considerations. The radiation field strength 1 m from the patient’s thyroid in units of air kerma (mGy/h) is
where 
is determined by a careful μSv/h measurement at 1 m from the patient’s thyroid taken t days (5–10 d) after administration of the 131I. Our primary mission here was to determine from this measurement the actual value of 
for this patient, thus removing the conservative aspect of the earlier estimate. When the equation above is solved for this parameter,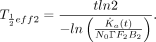
Eq. 7If Equation 7 yields a value for the half-life of 3 d or more, this value is accepted and the EXT worksheet is recomputed, providing updated restrictions. When Equation 7 yields a half-life of less than 3 d (3 d is considered a reasonable minimum value for the effective half-life for radioiodine release), a thyroid uptake value of less than F2 is suspected. When the equation for F2 is solved while maintaining the half-life at 3 d,
Eq. 8In summary, the EXT sheet of workbook 4 executes a protocol to determine a value for the rate at which 131I leaves this patient’s thyroid and, when needed, a new value for the thyroid uptake. The protocol is based on a careful measurement of the air kerma rate 1 m from the patient’s thyroid. Once this parameter is input along with the corresponding postadministration time, the resulting actual values of 
and F2 for this patient are computed and used in Equation 2 to reassess the initial restrictions placed on the patient’s interaction with children in the family.
Occasionally, to support maternal bonding, there is an urgency to gradually integrate the patient back into caring for an infant as effectively as possible. To deal with this, a second worksheet to workbook 4, labeled RATE, was introduced. The user tags each of 4 columns of the RATE sheet with patient-to-infant distances. For example, I usually tag the first column for bottle-feeding (0.1 m for the extrathyroidal cylindric source and 0.3 m for the thyroidal point source), the second column for bathing and diaper-changing (0.5 m), the third column for social interactions (1 m), and the fourth column for more remote duties the patient may have (3 m). Dose rates are then computed and displayed in each column for the corresponding user-specified distance. The dose rates have been computed using Equation 2 and averaged over each 24-h interval beginning with the 0th day and continuing through day 69. Next, the user or the patient enters a trial number of hours for each of the 4 patient-to-infant distances and for each 24-h interval. The workbook displays the doses that accumulate as a consequence. When the running total dose advances too rapidly, the user or patient returns to early times, and probably to short distances, to reduce the number of hours that had been previously tried. By repeatedly reconfiguring the trial number of hours, the patient develops a strategy that meets the selected dose constraint for the infant while most effectively addressing the perceived urgency.
The system is available free of charge via an email request to the author. This offer is basically “as is,” though the author will attempt to respond to requests and provide error corrections. The system will be forwarded to requesters by return email to include the 4 Excel workbooks, a user’s manual, and a document detailing the mathematics contained in the workbooks.
DISCUSSION
A reasonably comprehensive Excel-based system to evaluate and ensure the radiation protection of those in the vicinity of an 131I therapy patient has been presented. There are difficulties associated with some previous systems developed for this purpose, and in the course of developing the current product attempts have been made to address some of these. A frequent concern is that these methods tend to be overly conservative (7,8). In the approach presented here, the radiation emanating from the thyroid is modeled as a simple point source attenuated by a thickness of water-equivalent material specified by the user, whereas the extrathyroidal source is modeled as a cylindric volume 1-m long with nearly uniform source intensity throughout and incorporating self-absorption that corresponds to 364-keV photons in water. The user selects a diameter for the cylinder that can vary from 15 to 40 cm. The 15-cm-diameter source corresponds to a slender patient of youthful build whereas the 40-cm source corresponds to a large, possibly obese, patient and, as a consequence, will have greater self-absorption. The strength of these 2 sources is initially input as a total administered radionuclide activity that is partitioned by 2 corresponding uptake fractions that add to 1. The kinetic behavior of the radionuclide after administration is discussed in detail above. For hyperthyroid therapy cases, there is a large uncertainty regarding the rate at which the radionuclide leaves the thyroid by biologic transition. Occasionally the initial conservative estimate for this parameter may lead to oppressive restrictions. In this case, the system presented here has the patient return 5–10 d after administration to have this biologic rate constant measured. This process is simple, involving a single measurement with a radiation survey meter as discussed above. Although the corrected (measured) rate of escape from the thyroid often results in relaxation of the restrictions, the frequency of the relaxation being small is such that the initial estimates do not appear to be excessively conservative. It is usually dose limits to children in the family that prompt the patient’s return for this measurement, and the parents seem pleased with the assurance provided by the measurement that the children are being well protected. They are thankful, of course, whenever the restrictions are relaxed.
The selection of 1 m for the length of the cylindric source used to model the extrathyroidal compartment was somewhat arbitrary. Most individuals are closer to 1.7 m in length, and much of the extrathyroidal space is circulating blood, which is distributed over the entire body’s length. However, a shorter length for the cylinder is appropriate because the patient will be sitting much of the time, will not be completely straight while sleeping, and the radiation source strength may not be uniform along the entire body length. In estimating the effective length of the cylindric source, assumed to be uniform, 1 m was selected so that any error would be conservative. Modeling the extrathyroidal source as a cylindric volume rather than as a point is a dramatic step toward realism, whereas extending the length of the cylinder makes relatively little difference.
There is concern that Equation 2 may underestimate the dose to a child held by the patient. The child, being in direct contact with the abdomen/thorax of the patient, which is modeled as a cylindric volume source, is subject to a population of multiply scattered photons that differs from that of bystanders who are physically separated from the cylindric source. To assess this concern, the configuration of the 37 line sources within the cylinder was held constant as the cylinder was expanded by an annular ring of water (with no radioactivity) 20-cm thick. The air kerma midway within the annular ring, representing the dose point for the held child, was computed. Because the position of the child was now within the expanded cylinder, self-absorption was computed using buildup factors and the linear attenuation coefficient (9) rather than using the broad-beam half-value layer as before. The buildup factors were either computed by or verified by a Monte Carlo code to ensure that scattered photons were incorporated accurately. For this artificial worst-case scenario, the held-child doses increased by only 6.4% for the smallest cylinder and 13.4% for the largest (diameters, 15 and 40 cm, respectively). In the context of all the uncertainties inherent in the family counseling process, these variations are trivial and can be ignored.
Here I address concerns that assuming air kerma to be equivalent to effective dose may be excessively conservative. A Joint Task Group of the International Commission on Radiological Protection and the International Commission on Radiation Units and Measurements has provided effective dose–to–air kerma conversion factors as a function of bystander age and geometric orientation with respect to the beam (10). For the 364-keV photon and for children aged 0–5 y, the effective dose is 80%–90% of the air kerma for isotropic beam incidence (equal beam strength from all directions). For the adult bystander, a more appropriate beam orientation might be for the beam to be orthogonal to the adult’s longitudinal axis, but then rotate about this axis with no preferred direction. For this conformation of 364-keV photons incident on the adult bystander, the effective dose is about 82% of the air kerma. In both of these cases, the assumption that air kerma is equivalent to effective dose is conservative by only 10%–20%. However, if these photons were incident on the anterior of the child or the adult, the effective dose would be 110% of the air kerma. The latter configuration would be appropriate for a child being held by the patient, and possibly for the patient’s sleeping partner. Thus, assuming equivalence of effective dose and air kerma is not overly conservative, and in some cases it may fail to be sufficiently conservative.
As stated in the introduction, the worksheet that is central to the system presented here, the EXT sheet, is configured after one described previously (2). Although the 2 spreadsheets are similar in appearance, substantial differences between the 2 approaches exist. First, for the strength of the radiation field the method of reference (2) uses exposure measured at 2 distances from the patient (their example uses 0.3 and 1.0 m) immediately after administration of the radionuclide. This measurement incorporates the self-absorption present before the radionuclide has distributed. This initial source strength is then decayed by the effective half-lives corresponding to the biphasic retention. The method presented in this paper computes the source strength from the radionuclide activity remaining in the thyroid and the extrathyroidal space, reduced in intensity by the self-absorption computed separately for each of these compartments. The resulting source strengths of these 2 methods will differ substantially for hyperthyroid patients who have a large thyroidal iodine uptake because the self-absorption of radiation emanating from the thyroid is much less than that emanating from the patient immediately after administration. Second, the method of reference (2) is designed to be used when a therapeutic quantity of any radiopharmaceutical is used, whereas this paper is focused on the therapeutic use of 131I. Third, St. Germain et al. (2) suggest that uptake fraction and effective half-life for the thyroidal and extrathyroidal compartments be obtained either from relevant scientific literature or by actual measurement using a pretherapy tracer administration of the radiopharmaceutical to be used. The institution that originated the method described by St. Germain et al. (2) (Memorial Sloan Kettering, NY) prefers use of the pretherapy tracer, though this is not commonly used in most practices. The method of this paper uses a conservative estimate of effective half-life derived from data of the scientific literature combined with a measured thyroidal uptake as explained above. In addition to these 3 differences, the method of St. Germain et al. (2) has been expanded: first, to recognize the importance of reduced kidney function for the hypothyroid ablation patient relative to that of the patient prepared using thyrogen; second, to estimate the amount of radionuclide activity expelled at each urination; third, to provide updated restrictions based on a single measurement of radiation field strength 5–10 d after administration whenever the family finds the original restrictions to be oppressive; and fourth, to easily devise a personalized strategy to permit integration of the patient back into caring for an infant while complying with dose limits selected for the infant.
Both the EXT worksheet and the spreadsheet presented in St. Germain et al. (2) ignore dose to a bystander due to ingestion of radioactive contamination. When the bystander is a child (or pregnant woman) with a dose limit of only 1 mSv, and the family cannot sequester the child for a few days into a region of the household separated from that occupied by an ablation patient, this could become an issue. In such a situation, by ignoring internal dose the potential exists for the spreadsheets to mislead the counselor into believing that compliance is achieved, when in fact it may not be. (I have observed that infants’ mouths, when teething, are attracted by the cool, smooth texture of a toilet’s porcelain.) The INT sheet in the workbooks is intended, in part, to provide an alert regarding contamination potential.
CONCLUSION
The workbooks that were developed assist the radiation safety counselor in individualizing radiation protection procedures for the family of patients undergoing 131I therapy. The workbook system avoids overly conservative assumptions while permitting selection of appropriate dose limits for each individual.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Acknowledgments
The greatest contribution to the development of this product came from the patients and their families referred to me for radiation safety counseling. The sharing with me of their experience, circumstances, and concerns provided the direction and the motivation for developing the product. Richard T. Nelson, MD, and Kathleen Figaro, MD, are acknowledged for making the patient referrals and for their general support during project development. I particularly appreciate the efforts of Mark Madsen, PhD, for reviewing this work in an intermediate stage of development and for his comments and encouragement to share the work with the nuclear medicine community. I acknowledge my wife, Karen Beetham, PhD, who has corrected and improved multiple drafts of this paper, the user’s manual, and the document detailing the mathematics contained in the workbooks.
Footnotes
Published online Mar. 9, 2017.
REFERENCES
- Received for publication October 7, 2016.
- Accepted for publication February 25, 2017.
Jump to section
Related Articles
Cited By...
- No citing articles found.