Abstract
The aim of this study was to compare the performance of filtered backprojection (FBP) and ordered-subset expectation maximization (OSEM) reconstruction algorithms available in several types of commercial SPECT software. Methods: Numeric simulations of SPECT acquisitions of 2 phantoms were used: the National Electrical Manufacturers Association line phantom used for the assessment of SPECT resolution and a phantom with uniform, hot-rod, and cold-rod compartments. For FBP, no filtering and filtering of the projections with either a Butterworth filter (order 3 or 6) or a Hanning filter at various cutoff frequencies were considered. For OSEM, the number of subsets was 1, 4, 8, or 16, and the number of iterations was chosen to obtain a product number of iterations times the number of subsets equal to 16, 32, 48, or 64. The line phantom enabled us to obtain the reconstructed central, radial, and tangential full width at half maximum. The uniform compartment of the second phantom delivered the reconstructed mean pixel counts and SDs from which the coefficients of variation were calculated. Hot contrast and cold contrast were obtained from its rod compartments. Results: For FBP, the full width at half maximum, mean pixel count, coefficient of variation, and contrast were almost software independent. The only exceptions were a smaller (by 0.5 mm) full width at half maximum for one of the software types, higher mean pixel counts for 2 of the software types, and better contrast for 2 of the software types under some filtering conditions. For OSEM, the full width at half maximum differed by 0.1–2.5 mm with the different types of software but was almost independent of the number of subsets or iterations. There was a marked dependence of the mean pixel count on the type of software used, and there was a moderate dependence of the coefficient of variation. Contrast was almost software independent. The mean pixel count varied greatly with the number of iterations for 2 of the software types, and the coefficient of variation increased with the number of iterations for all types of software. The mean pixel count, coefficient of variation, and contrast were almost constant for a fixed product number of iterations times the number of subsets, whatever the number of subsets or iterations. Conclusion: Most of the types of software were equivalent for FBP or OSEM reconstruction. However, a few differences were observed with some types of software and should be considered when they are used.
For a long time, filtered backprojection (FBP) has been the only reconstruction algorithm used in SPECT. However, it appears that the more widely available and increasingly fast iterative reconstruction algorithm ordered-subset expectation maximization (OSEM) is being used progressively more often as a substitute for FBP (1–3). OSEM has the advantage over FBP of delivering images of a higher visual quality, especially in low-count areas (4). It also allows the correction of physical effects such as attenuation, scatter, or collimator depth–dependent resolution. However, unlike FBP, OSEM is not a linear algorithm, and the reconstructed contrast depends on the true contrast and on object size (5). Moreover, FBP is much faster than OSEM and remains widely used in clinical practice. FBP is also the reconstruction algorithm recommended for use in National Electrical Manufacturers Association (NEMA) performance tests (6).
FBP and OSEM are generally both available on all SPECT processing workstations developed by γ-camera manufacturers or by nuclear medicine processing software companies (7). There are 2 FBP schemes (2,8). One uses the Fourier transform, and the other uses the convolution product. Although mathematically equivalent, the 2 schemes differ when numerically computed. The various implementations of OSEM are also likely to differ. For example, OSEM generates pixels with very high counts, especially at the image borders (4), and scaling of the final reconstructed data is needed. No consensus seems to exist on the way to limit the phenomenon of high counts or on the way to perform scaling. Another example of a possible difference between the various implementations of OSEM is the way to divide the projections among the subsets (4). As a consequence of all of these differences, the results of patient studies and SPECT camera performance could depend on the type of reconstruction software used.
Compared with the requirements of PET, the reconstruction of SPECT data need not necessarily be performed with the software provided by the scanner manufacturer. The reason stems partly from the fact that a scanner's intrinsic corrections are all made online in SPECT, whereas they are performed mainly during the reconstruction step in PET, and partly from the fact that corrections for physical effects such as attenuation, scatter, and resolution are generally not performed in SPECT (at least this was the case before the recent introduction of hybrid SPECT/CT scanners). In Europe, it is not uncommon to find SPECT cameras not connected to the processing systems proposed by their manufacturers. For example, the use of γ-cameras from different vendors and a unique processing system, a processing system not upgraded with the purchase of a new camera, an upgrade of a processing system without replacement of the camera, and the use of a processing system from a software-only company are all quite frequently occurring situations in European nuclear medicine departments. It is therefore worthwhile to investigate the effect of the processing software on the reconstructed data.
The aim of this study was to compare the FBP and OSEM algorithms implemented in their current and previous workstations by the 3 current major manufacturers of γ-cameras (GE Healthcare, Philips, and Siemens) and by one software company (Segami). Three filters, namely, ramp, Butterworth, and Hanning, were used for FBP, and the numbers of subsets and iterations were varied in OSEM. Spatial resolution, pixel count, noise level, and contrast in the reconstructed slices of line, uniform, and hot- and cold-rod phantoms were the parameters considered in the study.
MATERIALS AND METHODS
SPECT Data
The SPECT projections used in the present study were numeric simulations of 2 phantoms. The first one represented the line source used in the NEMA SPECT spatial resolution test (6). The projections were downloaded from the Web database of the Monte Carlo emission tomography project (9). They were issued from a Monte Carlo simulation. The simulated camera was the dual-head Elscint Helix fitted with low-energy high-resolution collimators. Two source locations were considered: on the camera rotation axis and 9 cm off the axis. The rotation radius was 15 cm, the projection matrix included 128 × 128 pixels, and the pixel size was 2 mm.
The second phantom was a cylinder with a 20-cm diameter. It comprised 3 different compartments (Supplemental Fig. 1) (supplemental materials are available online only at http://tech.snmjournals.org). The first one was a cylindric, uniformly emitting compartment with a height of 8 cm. The second compartment consisted of cold rods in a hot background, and the third one consisted of hot rods in a cold background. Both compartments comprised 7 rods that were 8.5 cm high. The rods were parallel to the cylinder main axis. The largest rod was centered on the cylinder main axis; the 6 others were equally spaced, and their axis was 5 cm from the cylinder main axis. The diameters of the cold rods were 25, 20, 16, 12, 10, 8, and 6 mm, and the diameters of the hot rods were 20, 16, 13, 10, 8, 6, and 5 mm. This phantom is used for routine quality control of various SPECT cameras.
To build a numeric version of the second phantom, we obtained SPECT acquisitions of the phantom filled with an aqueous solution of 740 MBq of technetium on several double-head cameras with a projection pixel size of 2.8 ± 0.1 mm. They were reconstructed with FBP (ramp filter) and Chang attenuation correction (10). The numeric phantom was designed by use of the mean number of counts per pixel found on the reconstructed slices as well as the size and shape of the physical phantom. The specific activities in the uniform compartment, in the hot rods, and in the background region of the compartment with the cold rods were identical. The specific activities in the cold rods and in the background region of the compartment with the hot rods were 10 times lower. This activity simulated the scattered activity in these cold areas that was observed on the real phantom images. Simple forward projection (no attenuation and no scatter), convolution by a gaussian filter of 8-mm full width at half maximum (FWHM), and the addition of Poisson noise allowed us to obtain the simulated SPECT dataset. The projection matrix was 128 × 128 pixels, and the pixel size was 2.8 mm. Simulated SPECT data were stored in both Interfile and DICOM files, which allowed their transfer to the various workstations used in the study.
Workstations
The following workstations (Table 1) were included in the study: GE Healthcare Xeleris and Vision (formerly from Sopha Medical Vision), Philips Jetstream, Segami Mirage, and Siemens eSoft and Icon. For comparison, Sopha Medical Vision XT processing software running on a Sopha Medical Vision DST camera acquisition computer was also considered. This software was available on NXT workstations as well as on DST and DSX cameras produced during the 1990s by Sopha Medical Vision.
FWHMs, Mean Pixel Counts, and COVs for Reconstruction of Unfiltered Projections of Line or Uniform Cylinder Phantoms with Various Nuclear Medicine Workstations
FBP Reconstructions
FBP reconstructions were performed by use of the ramp filter limited at the Nyquist frequency (0.5 cycle per pixel). Prefiltering of the projections with either the Hanning filter or the order 3 or 6 Butterworth filter was also considered. Three cutoff frequencies (0.20, 0.35, and 0.50 cycles per pixel) were used with the Hanning filter, and 4 cutoff frequencies (0.10, 0.20, 0.35, and 0.50 cycles per pixel) were used with the Butterworth filter. The order 3 Butterworth filter did not exist on the Mirage workstation. It was also observed that there were 2 definitions of the Butterworth filter. The difference was a square root in the filter formula. It emerged that the cutoff frequency was the frequency for which the filter was equal either to 0.5 (definition without square root) or to half the square root of 2 (definition with the square root) in the Fourier space (7). The curves in the Fourier space obtained with both definitions are illustrated in Supplemental Figure 2 for the order 6 Butterworth filter at a cutoff frequency of 0.2 cycle per pixel. With some workstations it was even possible to switch between the 2 formulas, but only one arbitrarily chosen formula was used in the study. The definition with the square root, which is the correct definition for the Butterworth filter (7), was used on the Mirage, Xeleris, and XT systems and the definition without the square root on the others. Great care was taken to have the same scaling factor applied to all FBP reconstructions performed with the same workstation.
OSEM Reconstructions
The number of subsets for OSEM reconstruction was 1, 4, 8, or 16. The number of iterations was chosen to obtain a product number of iterations times the number of subsets equal to 16, 32, 48, or 64. When a choice was proposed, the output was always set to “quantitative.”
For the Xeleris workstation, OSEM-Genie and OSEM-SMV were used. OSEM-Genie is the software previously implemented by GE Healthcare in the Genie workstation. OSEM-SMV is the software implemented by Sopha Medical Vision in the Vision workstation before GE Healthcare took over Sopha Medical Vision. For the Jetstream workstation, OSEM-3D (Jetstream 3D) was used, but reconstructions with one subset were also performed with the MLEM-2D package (Jetstream 2D). Both MLEM-2D and OSEM-3D were developed by ADAC before Philips took over the company. With the Mirage workstation, only 1 or 4 subsets were available, and OSEM is part of the Respect package. Great care was taken to ensure that the various and numerous options (attenuation correction, scatter correction, resolution recovery, and noise regularization) of this package were not activated. OSEM was not available on Siemens Icon or Sopha Medical Vision XT. Despite numerous attempts, we did not succeed in iteratively reconstructing our data with Siemens eSoft, although the files seemed to be correctly imported into the system and could be reconstructed with FBP. The eSoft OSEM algorithm seemed not to recognize the number of projections or the angle between consecutive projections.
Analysis of Results
Reconstructed slices were saved as either Interfile or DICOM files and were imported for further analysis to “A Medical Image Data Examiner” (AMIDE, version 0.8.19; Andy Loening) freeware running on a Macintosh (Apple) laptop computer. For the lines, 3 transverse slices were selected: one at midline and the others at ±5 cm from the midline. The AMIDE profile tool was used to obtain, along the image x-axis and y-axis, the reconstructed FWHM and full width at tenth maximum (FWTM) as well as the peak profile position. The peak profile position was considered to be the line position along the axis. For the line centered on the camera rotation axis, the FWHM or FWTM values measured along the 2 axes were averaged to obtain the central FWHM or FWTM. For the off-axis line, the values measured along each axis were identified as the radial or the tangential FWHM and FWTM. Finally, the corresponding values (FWHM, FWTM, or line position) obtained at the 3 line positions were averaged. FWTMs always behaved in a manner similar to that of FWHMs and were not considered further. A cylindric region of interest (ROI) with a 30-pixel diameter and a height of 11 slices was centered in the reconstructed uniform phantom images and stored in AMIDE. The AMIDE ROI statistics tool was used to obtain the mean pixel counts and SDs in the ROI. The coefficient of variation (COV) was calculated from the ratio of the SD to the mean. Two cylindric ROIs with a height of 11 slices, one with the rod diameter and one with half the rod diameter, were drawn in the middle part of each rod in both rod compartments. Six rods with a 6-pixel diameter and a height of 11 slices were positioned between the rods in both rod compartments and served as background ROIs for each compartment. All ROIs were stored in AMIDE. The AMIDE ROI statistics tool was used to obtain the mean pixel count in each ROI. The values of the 6 background ROIs were averaged and this mean value was used as the compartment background value. The following formulas were used to compute hot contrast (HC) and cold contrast (CC): HC = (NH/NB) – 1 and CC = 1 – (NC/NB). In these formulas, NH is the mean number of counts per pixel in the hot-rod ROI, NB is the mean number of counts per pixel in the compartment background, and NC is the mean number of counts per pixel in the cold-rod ROI.
RESULTS
Table 1 shows the central, radial, and tangential FWHMs when FBP was applied to unfiltered projections. Figures 1 and 2 show the same parameters when FBP was applied to projections processed with the Hanning filter or the order 6 Butterworth filter. The trends in the curves with the order 3 Butterworth filter and the order 6 Butterworth filter were identical. The positions of the lines in the transverse plane were identical (within 0.1 pixel) for all but one type of software: with Vision, the line position was shifted by +0.5 pixel in both plane directions. The mean pixel counts and COVs of the uniform slices are shown in Table 1 for FBP reconstruction of unfiltered projections. Prefiltering of the projections with either the Hanning filter or the Butterworth filter changed the reconstructed mean pixel counts, as shown in Figure 3, and lowered the COVs (data not shown). For a given filter and a fixed cutoff frequency, the COV was found to be almost software independent. The same observation applied to HC and CC except in the following situations. For FBP reconstruction of unfiltered projections with Vision, slightly higher contrast (5%−7% for both ROI sizes) was observed for the 2 largest hot rods. For Vision, HC was higher when filtering the projections with the Hanning filter (Fig. 4). This held true for XT when the cutoff frequency of the Hanning filter was 0.35 or 0.20 cycle per pixel (Fig. 4). For Vision, CC was slightly higher when filtering the projections with the Hanning filter at a cutoff frequency of 0.2 cycle per pixel (Fig. 4). Filtering of the projections with the Butterworth filter at a cutoff frequency of 0.1 cycle per pixel led to higher HC and CC for Mirage, Xeleris, and XT and to slightly higher HC for Vision (data not shown). With the Hanning filter, contrast was reduced with a decrease in the cutoff frequency (Fig. 4) for all types of software. A reduction in contrast was also observed for all types of software with the Butterworth filter when the cutoff frequency fell below 0.20 cycle per pixel.
Central (A), radial (B), and tangential (C) FWHMs for FBP reconstruction of projections filtered with Hanning filter at 3 cutoff frequencies. cy/px = cycles per pixel.
Central (A), radial (B), and tangential (C) FWHMs for FBP reconstruction of projections filtered with order 6 Butterworth filter at 4 cutoff frequencies. cy/px = cycles per pixel.
Percentage difference (Diff) in mean pixel counts between FBP reconstruction of projections filtered with Hanning (Hann) filter or Butterworth (But) filter and FBP reconstruction of unfiltered projections (ramp reconstruction). First digit after “But” indicates order of Butterworth filter. Last 2 digits after filter name abbreviation indicate 100 times cutoff, or cutoff frequency of cycles per pixel (e.g., “35” represents “frequency of 0.35 cycle per pixel”).
Contrast for hot (A–C) and cold (D) rods for FBP reconstruction of projections filtered with Hanning filter at cutoff frequencies of 0.2 (A and D), 0.35 (C), and 0.5 (B) cycles per pixel. For Jetstream, eSoft, Icon, Mirage, and Xeleris, values for contrast were almost identical, and only mean value for these 5 types of software is reported. SD was below 4%; error bars were smaller than square symbols and were omitted for clarity. CC for cutoff frequency of 0.35 or 0.5 cycle per pixel was found to be software independent.
Central, radial and tangential FWHMs for OSEM reconstruction with different numbers of subsets and iterations are shown in Figure 5. The positions of the lines in the transverse plane were identical (within 0.1 pixel) for all but one type of software: with Vision, the line was shifted by +1 pixel in x-direction and by −1 pixel in y-direction. The mean pixel counts depended on the software used (Table 1) and on the number of subsets and iterations (Fig. 6). The COV increased with the number of iterations (Fig. 7). However, for a fixed number of subsets times the number of iterations, the COV remained almost independent of the number of subsets with the exception of the OSEM-Genie, for which it increased with the number of subsets. Contrast improved with an increase in the number of subsets times the number of iterations but was found to be almost software independent (data not shown). For a fixed number of subsets times the number of iterations, contrast remained almost independent of the number of subsets for all types of software.
Central (A), radial (B), and tangential (C) FWHMs for OSEM reconstruction with various numbers of subsets (s) and iterations (i). Some combinations were not available for some types of software.
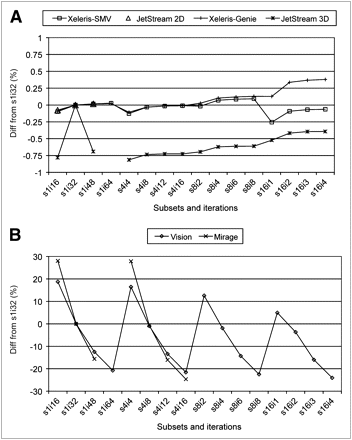
Percentage variation (Diff = difference) of mean pixel counts from value obtained with 1 subset and 32 iterations for all combinations of numbers of subsets (s) and iterations (i) used in this study. Some combinations were not available for some types of software. (A) Jetstream and Xeleris. (B) Mirage and Vision.
COVs of uniform slices reconstructed with various numbers of subsets (s) and iterations (i). Some combinations were not available for some types of software.
DISCUSSION
SPECT plays an ever-growing role in scintigraphy. Unlike planar imaging, SPECT requires the processing of the acquired data, that is, the reconstruction step, to obtain the images (1,2). Each γ-camera manufacturer and several software companies have developed nuclear medicine processing workstations. Today, they all offer 2 SPECT reconstruction methods, namely, FBP and OSEM (7). Their numeric implementations are likely to differ from workstation to workstation because of the use of different forms of hardware, operating systems, programming languages, and algorithms. Therefore, the results from phantom and clinical studies could also depend on the workstation being used to reconstruct the SPECT data. The visualization or the subsequent processing of the SPECT reconstructed images is highly influenced by their spatial resolution, noise level, and contrast. This information guided the choice of 4 parameters measured in the present study: the FWHM of a line source, the COV of a uniform phantom, the contrast of hot rods, and the contrast of cold rods. Within the framework of quantification, the number of reconstructed counts is also important. This was the fifth parameter investigated. Line and point sources in a null background are not well suited for maximum-likelihood expectation maximization (MLEM) or OSEM because of the nonnegativity constraint of these algorithms. Although FBP is the recommended method, NEMA SPECT performance tests (6) do allow the use of iterative algorithms for resolution assessment with this kind of source. This information directed us toward using line sources with OSEM reconstruction in the present study.
It was decided to include in the study the most recent workstations of the 3 major γ-camera suppliers (GE Healthcare, Philips, and Siemens) as well as some of their older systems on the basis of availability and image transfer possibility. We were also able to investigate a workstation developed by a software-only company (Segami). Some of the tested types of reconstruction software were developed by companies like Sopha Medical Vision or ADAC before their respective takeovers by GE Healthcare and Philips. These types of software are likely to be identical to the types of software available on the workstations sold in the past by the companies that developed them. However, such identity is difficult to guarantee without further testing because of the differences in hardware and operating systems used as well as the possible corrections of “bugs.” The OSEM algorithms of Vision and Xeleris (OSEM-SMV) illustrated this last point, as discussed later.
We deliberately chose to use as many data as possible from Monte Carlo simulations in the Monte Carlo emission tomography database (9) and a form of analysis software (AMIDE) freely available on the Web. In this way, interested readers could easily reproduce the experiments using their own workstations. The uniform and contrast phantom was the only exception. We used this phantom because the present study is part of a larger project assessing performance in SPECT, including comparisons of γ-cameras (11). The numeric uniform phantom mimics the real phantom used for these comparisons. This phantom is easy to reproduce because no sophisticated simulation is needed. Moreover, any other phantom would be convenient to use, as one would just have to compare the numbers of reconstructed counts and the reconstructed contrast with the true numbers of counts and the true contrast. The uniform and contrast phantom data are available on request.
The measurements of spatial resolution and noise level for the FBP-reconstructed images were almost identical for most of the types of software (Table 1). Differences were observed only in the FWHM obtained with Vision (about 0.5 mm smaller) and in the COV obtained with XT (about 15% higher). We could find no explanation for the smaller FWHM found with Vision. The higher COV found with XT could have resulted from the use of integers instead of floats in this old system. Prefiltering of the projections with the widely used Butterworth filter or Hanning filter (3,7) also led to similar FWHMs (Figs. 1 and 2), except again in the case of the Vision FWHMs and the XT COVs (data not shown). The other visible differences shown in Figures 1 and 2 or observed in the COVs (data not shown) originated from the formula used to define the Butterworth filter. Indeed, for a given cutoff frequency and a given order, the formula with the square root (Mirage, Xeleris, and XT) leads to a less smoothing filter than the formula without the square root (eSoft, Icon, Jetstream, and Vision). This difference is illustrated in Supplemental Figure 2. Consequently, the FWHMs are smaller (Figs. 1 and 2) and the COVs are higher when the Butterworth filter is defined with the formula including the square root. The reconstructed pixel counts for Vision (2,958) and XT (1,068) were found to differ from those for all other workstations (375.9 ± 1.2). We have no definitive explanation for this finding. However, it was observed that both the Vision and the XT systems applied a scaling factor, probably to avoid any overflow during the reconstruction process. It is possible that the output is not corrected for this factor after the reconstruction. Contrast was found to be almost software independent, except in a few situations. With the Hanning filter, HC was found to be enhanced for Vision at all cutoff frequencies and for XT when the cutoff frequency became lower than 0.35 cycle per pixel (Fig. 4). CC was higher for Vision and the Hanning filter at a cutoff frequency of 0.20 cycle per pixel (Fig. 4). The Butterworth filter at a cutoff frequency of 0.1 cycle per pixel led to slightly higher HC for Vision and to higher HC and CC for Mirage, Xeleris, and XT. Inspection of Figures 1 and 2 shows that the contrast enhancements corresponded to situations in which the FWHMs were lower by more than approximately 0.5 mm for the hot rods and by more than 1 mm for the cold rods. It is important to note that the filter cutoff frequencies used in the present study covered a larger range than the frequencies used in clinical settings.
For OSEM reconstruction, a greater variability between the types of software was observed for the measured FWHMs (Fig. 5), mean pixel counts (Table 1), and COVs (Fig. 7). Although limited to 0.5–1 mm for most of the types of software, the differences in the FWHMs (Fig. 5) could amount to 2.0–2.5 mm for Mirage and Xeleris with OSEM-Genie. With the exception of Xeleris with OSEM-Genie, the FWHMs depended slightly on the choices of the numbers of subsets and iterations. The FWHMs were generally lower with OSEM reconstruction than with FBP reconstruction. The mean pixel counts (Table 1) depended largely on the software used and varied greatly (Fig. 6) with the number of iterations for Mirage and Vision. This point is particularly relevant where these types of software are used in quantitative studies. For example, the calibration factor needs to be determined for each combination of iterations and subsets when data are iteratively reconstructed with Mirage or Vision. The COV (Fig. 7) and the contrast (data not shown) increased with the number of iterations, as expected for OSEM (12). However, at a fixed product number of subsets by number of iterations (i.e., at a fixed number of equivalent MLEM iterations), the COV and the contrast were found to be almost independent of the selected combinations of subsets and iterations for most of the types of software, except OSEM-Genie on Xeleris. Examination of the FWHM results (Fig. 5) and the images (not shown) revealed that OSEM-Genie on Xeleris appeared to behave poorly with a small number of subsets and provided images more comparable to those obtained with the other types of software when 8 or 16 subsets were used. The COVs were noticeably lower for Jetstream OSEM-3D than for the other types of software. However, it should be remembered that all of the other types of software are 2-dimensional reconstruction algorithms. The Jetstream OSEM-3D software was included in the study because of the absence of OSEM-2D in this workstation. It is also important that the numbers of subsets and iterations used in the study cover the range of values usually adopted in clinical settings. When one subset was used, OSEM was virtually converted to MLEM (4). It should be remembered that the convergence of the iterative process could be mathematically demonstrated for MLEM but not for OSEM and that ordered subsets remain a heuristic way of speeding up the iterative process (4).
It is also interesting to compare the results obtained with OSEM on Vision and OSEM-SMV on Xeleris. It is clearly stated in the on-screen information available on Xeleris that both workstations use the same OSEM algorithm. Although the measured FWHMs (Fig. 5) were very close for the 2 workstations, the shifts in source location (one pixel) and the large variations in the mean pixel counts (Fig. 6) observed for Vision disappeared with Xeleris. This finding indicates that the results obtained in the present study should not be extended to any other workstation without further testing, even if it is claimed that the reconstruction algorithms are the same.
NEMA procedures recommend the use of FBP to assess SPECT resolution performances of γ-cameras (6). Except with Vision, the results would not depend on the reconstruction software used (among those included in the present study). For other types of software, we would recommend that our experiments be reproduced and that the obtained FWHMs be compared with those presented here (Table 1). The use of OSEM for the FWHM determination, as allowed in the NEMA procedures (6), would lead to a dependence of the measured values on the workstation used to perform the reconstruction. Therefore, in addition to the reconstruction technique used, as stated in the NEMA procedures (6), the workstation and the software version used would also need to be specified with the results.
Finally, it is interesting that although a decrease of at least 0.5 (1) mm in the FWHM translated to an increase in HC (CC) when the reconstruction was performed with FBP, this was not observed for OSEM reconstructions. For example, the iterative reconstructions with Mirage led to FWHMs that were 1–2 mm lower but not to enhanced contrast. Because of its nonnegativity constraint, OSEM is not suited for FWHM measurement with a line source in a null background, and NEMA, for example, recommends the use of FBP for FWHM measurement with line or point sources in air (6).
CONCLUSION
Most of the types of software tested were equivalent for FBP reconstruction: the values for resolution, noise level, and contrast were almost identical. Nevertheless, using the Vision for FBP reconstruction of a SPECT resolution test led to an FWHM that was 0.5 mm smaller. It was also observed that there were 2 definitions of the Butterworth filter. For a fixed order and a fixed cutoff frequency, one definition led to a less smoothing filter, which resulted in higher noise levels and smaller FWHMs. However, differences in the FWHM translated to differences in contrast only when they exceeded 0.5 mm for the hot rods and 1 mm for the cold rods. When considering the FWHM and noise level, more noticeable differences between the workstations were observed for OSEM reconstruction. However, HC and CC were found to be almost software independent. Care should be taken before extending this observation to any contrast that might be encountered in clinical studies because OSEM-reconstructed contrast is known to depend on the true contrast and on object size (5).
All of the software types used in the present study behaved as expected: lowering the filter cutoff frequency in FBP resulted in larger FWHMs and in lower noise levels and reduced contrast; increasing the product number of subsets times the number of iterations in OSEM resulted in improved contrast and higher noise levels. The measured parameters generally did not depend on the choice of the number of subsets (with at least 4 projections per subset) or iterations for a fixed product number of subsets times the number of iterations. The OSEM-Genie on Xeleris constituted an exception to this rule for all of the measured parameters, and the same was true with OSEM on Vision and Mirage for the reconstructed mean pixel counts.
Acknowledgments
We are pleased to acknowledge V. Bartholome (GE Healthcare), M. Guerschaft (Philips), and Dr. Christian Vanhove (UZB Brussels) for their help in using the GE Healthcare, Philips, and Siemens workstations, respectively. We are also grateful to the reviewer who suggested the inclusion of contrast measurements.
Footnotes
-
COPYRIGHT © 2009 by the Society of Nuclear Medicine, Inc.
References
- Received for publication December 17, 2008.
- Accepted for publication May 19, 2009.