Abstract
Data acquisition is substantially different in PET than it is in planar nuclear medicine and SPECT. There is an entirely different set of definitions and considerations. The objective of this paper is to provide the reader with the terminology and understanding of how PET data are acquired and organized as well as the issues involved in choosing one approach over another. Sinograms and projection views will be presented as methods of storing and viewing raw PET data. Different approaches to increase axial sampling while maintaining a sufficient number of counts for each reconstructed slice are discussed, as well as the use of sinogram compression or “mashing” to reduce the storage requirements of raw PET data. The differences between 2-dimensional (2D) and 3-dimensional (3D) PET and how storage of raw 3D data may differ from that of 2D data are described. The concept of “Michelograms” as a means of displaying the nature of the axial sampling in both 2D and 3D PET is discussed. After reading this paper, the reader will be able to describe 2 methods used to store and display raw PET data and compare them with methods used in SPECT. The reader will be able to define the terms “span” and “maximum ring difference” and describe how they relate to the axial sampling in 2D and 3D PET. The reader will also be able to list 3 ways in which 3D PET differs from 2D PET.
In PET, annihilation coincidence detection is used in lieu of absorptive collimation to determine the directionality of the detected photons. Because of this, the sensitivity of PET is substantially higher than in conventional, single-photon nuclear imaging. Because the detection of PET data is fundamentally different from conventional nuclear imaging, the manner in which it is handled is also substantially different. There are also different ways to combine the data to further reduce the noise in the resultant reconstructed images. These distinctions lead to new considerations with respect to data acquisition. Two basic ways to collect PET data are referred to as 2-dimensional (2D) and 3-dimensional (3D) PET. Some PET scanners can acquire data in both 2D and 3D modes whereas others can only acquire data in 3D mode. Some older scanners may only acquire data in 2D mode. The acquisition of 3D PET has its own unique considerations. We will discuss how PET data, both 2D and 3D, are acquired and how PET differs from single-photon imaging.
We will first briefly review the basics of PET imaging. Consider a patient who has been injected with a positron-emitting radiopharmaceutical such as 18F-FDG. One of the 18F atoms will decay with the emission of a positron. After traveling a short distance (possibly several millimeters in tissue), the positron will combine with an electron, and the two will undergo an annihilation such that their masses are converted to energy in the form of 2 photons being emitted back-to-back. If these 2 photons are simultaneously detected by 2 small detectors, we can infer that the annihilation must have occurred along the line connecting the 2 detectors. This line is referred to as the “line of response,” or “LOR.” To increase the sensitivity of the scanner, the object is surrounded by a “ring” of small detectors rather than only 2. Such a ring is shown in Figure 1A. To image multiple planes simultaneously, several such rings are placed back-to-back. It is therefore convenient to organize the detectors into 2D arrays, called detector “blocks,” where the detectors along the x-axis go around the ring and those in the y-direction go axially into the ring. An array of photomultiplier tubes are placed behind the detector block to collect the scintillation light and determine within which detector the event occurred. An alternative to this approach implemented by some vendors is the use of opposing, large-area continuous detectors. The scanners using continuous detectors typically have 3 sets of opposing detectors (6 detectors in all) forming a complete ring about the patient. There are several excellent references for those desiring a more complete introduction to PET instrumentation (1,2). Because most current PET scanners use the block-based ring design, we will assume this design for the rest of this paper.
Sinogram formation. Coincidence events in PET scanner are categorized by plotting each LOR as function of its angular orientation versus its displacement from center of gantry. (A) Center of gantry is noted by cross (X), and locus of interest (e.g., tumor) is noted by ellipse. Four LORs passing through locus of interest are labeled A, B, C, and D. (B) These 4 LORs are plotted on this sinogram where angular orientation is on y-axis and displacement from center of gantry is on x-axis. If all possible LORs that pass through this point are plotted, it maps out half of sine wave turned on its side as shown here. (C) Sinograms of more complicated objects, such as sinogram of brain scan shown, are composed of many overlapping sine waves. (D) Reconstructed brain image corresponding to sinogram in (C) is shown.
THE SINOGRAM
Consider a patient who has a small tumor in the anterior portion of the brain as shown in Figure 1A (ellipse) undergoing imaging with a ring-style PET scanner. The center of the PET gantry is also noted in the figure with a cross (X). A PET agent that localizes in the tumor has been administered to the patient. Let’s assume a positron is emitted from the tumor and annihilates with an electron leading to a coincidence detection as noted by “A” in Figure 1A. This coincidence detection is characterized by the LOR that connects the 2 detectors involved in the detection. The LOR is characterized by the angle of orientation of the LOR and the shortest distance between the LOR and the center of the gantry. This is plotted in Figure 1B where the angle of orientation (0o in case of the LOR marked A) is plotted on the y-axis, and the shortest distance between the LOR and the center of the gantry is plotted on the x-axis. Three other coincidence detections are characterized by 3 other LORs (B, C, and D) at different angles and distances as shown in Figure 1A. These points are also plotted in Figure 1B. If a large number of LORs are plotted from the same point (or pixel), the resulting graph is half of a sine wave turned on its side, as shown in Figure 1B. This graph is appropriately referred to as a “sinogram.” The location of the point in the transverse plane (e.g., the location of the tumor in Fig. 1A) can be determined from the sinogram. The distance of the point from the center of the gantry can be determined from the amplitude of the sine wave, and its angular location from the phase of the sine wave. A more complicated object will cover many pixels, and thus, its sinogram will consist of a large number of overlapping sine waves. A sinogram of a PET slice through the brain and its corresponding transverse reconstruction are shown in Figures 1C and 1D, respectively. PET data are acquired directly into sinograms in a manner similar to matrix mode in planar imaging. Each detector pair (and thereby each LOR) corresponds to a particular pixel in the sinogram depending on its orientation angle and distance from the center of the gantry. Therefore, for each coincidence detection, the LOR for that detection is determined, the pixel in the sinogram associated with that LOR is located, and the value in the pixel is incremented. In the final sinogram, the value in each pixel represents the number of coincidence detections between the detector pair associated with that LOR. A separate sinogram is acquired for each slice that is to be reconstructed.
The values along a particular horizontal row in the sinogram represent detections acquired along parallel LORs at the angle that corresponds to that row. This is illustrated for 3 rows corresponding to 3 projection angles in Figure 2. Each pixel value along the row is the sum of all of the events acquired along the corresponding LOR. Such a collection of LOR sums is referred to as a “projection.” Each row in the sinogram is the projection of that slice along the angle associated with that row. Comparing the raw data acquired in PET to that in SPECT, each projection image in SPECT represents the data acquired at that projection angle across all slices, whereas in PET each sinogram represents the data acquired for that slice across all projection angles. The set of sinograms from a complete, multislice PET study can be easily reorganized in the computer to generate a series of projection “views” that would be similar to the raw data acquired in SPECT. In this way, raw PET data can be presented as either a series of sinograms with a separate sinogram for each slice (Fig. 3A), or as a series of projection views with a separate view for each projection angle (Fig. 3B).
Sinograms and projections. Plot of LOR sums from series of parallel LORs at particular angle is referred to as “projection.” Figure shows projections through object at 3 different angles (−90o, −5o, and 45o). Each row in sinogram is projection through object at that angle. For example, row through sinogram at –5o is composed of projection through object at –5o.
Sinograms and views. Two alternative methods of displaying raw PET data are sinograms and projection views. (A) Sinogram displays all angles for particular slice with separate sinogram for each slice. (B) Alternatively, each projection view displays all slices at particular projection angle with separate view for each angle. Complete set of sinogram data can be easily reconfigured and displayed as projection views and vice versa.
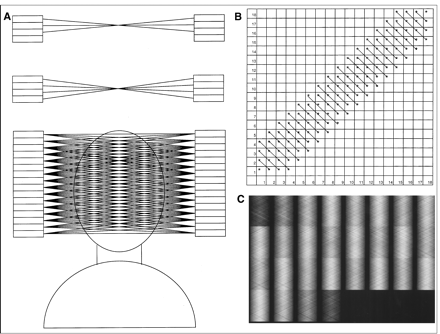
Consider the simple ring detector in Figure 4A. The data associated with a particular detector, say a detector in Block 12, are located along a diagonal in the sinogram (Fig. 4B). Those events involving detectors with which Block 12 is in coincidence, Blocks 1−7, are also located on diagonals slanting in the opposite direction. Coincidence events involving a detector in Block 12 and a detector in Block 4 are located in the pixel at the intersection of the 2 diagonals as shown in Figures 4A and 4B by the dashed lines. For quality control, a PET scan can be acquired with either a uniform source or a moving source that uniformly irradiates the detectors. If a particular detector is not working properly, it will lead to a diagonal streak across the sinogram. Figure 4C shows a sinogram acquired with a uniform source with a diagonal streak across it, indicating that one of the detector blocks is malfunctioning. The operator can determine which detector is having problems by the location of the streak.
Sinograms and ring gantry. (A) Ring gantry is shown with 16 detector blocks. (B) In sinogram, events involving Block 12 are displayed along diagonal as shown. All blocks in coincidence with Block 12 (Blocks 1−7) are also displayed along diagonals, but slanting in opposite direction. LOR shown in (A) as dashed line is represented in sinogram in (B) as intersection of dashed lines from Block 12 and Block 4, respectively. (C) If particular block in scanner is malfunctioning, it will lead to diagonal streak in sinogram as shown here. This fact is used in routine PET quality control to determine which blocks may need to be serviced.
As previously discussed, events along a particular row in the sinogram represent those associated with parallel LORs. However, due to the curved nature of the detector ring, those LORs passing near the center of the gantry will be spaced farther apart than those LORs on the periphery, as shown in Figure 5. Simple reconstruction algorithms will assume that these LORs are evenly spaced, and so a correction must be applied to compensate for this variation in LOR spacing. This is referred to as “arc correction” because it corrects for the fact that the detectors are located on an arc. Arc correction is typically applied before reconstruction and is more important for large objects, where some of the LORs are far from the gantry center, than it is for small objects. Arc correction is also more important for small-bore scanners (e.g., dedicated brain or small-animal devices) than it is for whole-body scanners.
Arc correction. Figure shows all parallel LORs at 90o. Due to curved nature of gantry, LORs toward periphery are more closely spaced than those toward center. Correction is applied before reconstruction to address this differential spacing known as “arc correction.” Note that arc correction is more prominent for either large objects (part of object imaged far from gantry center) or small gantries.
To summarize, PET raw data are acquired directly into sinograms. In the sinogram, the LOR associated with each coincidence detection is plotted as a function of angle of orientation versus the shortest distance between the LOR and the center of the gantry. There is a separate sinogram for each slice containing the projection data across all projection angles. These data can be reorganized into projection views where each image represents the projection data for all slices. A particular pixel in the transverse image plots into half of a sine wave in the sinogram. Conversely, each pixel in the sinogram corresponds to a particular LOR or detector pair. Events associated with a particular detector are plotted on diagonals across the sinogram. Thus the sinogram of a uniform source can be used for scanner quality control.
Michelograms, Span, and Sinogram Mashing
Figure 6 shows a cross-section through the gantry of a ring-style scanner. Consider the scanner illustrated in Figure 6A has 16 detector rings with a center-to-center spacing of 6 mm. The axial direction into the gantry is in the vertical direction in this figure. If detectors on one side of the gantry are only allowed to be in coincidence with detectors on the opposite side of the same ring, the detected coincidence events are referred to as “direct” coincidences as shown in Figure 6A. In this case, detectors in Ring 1 are only in coincidence with detectors in Ring 1, detectors in Ring 2 only with Ring 2, and so on. This leads to 16 reconstructed planes with a 6-mm, center-to-center spacing. To improve the axial sampling and slice sensitivity, detectors can be allowed to be in coincidence with detectors in neighboring rings, referred to as “cross” coincidences. That is, the data from Ring 1 in coincidence with Ring 2 are combined with the data in Ring 2 in coincidence with Ring 1. Combining direct and crossed coincidences as shown in Figure 6B leads to 16 direct coincidence planes and 15 cross planes for a total of 31 transverse planes spaced 3 mm apart. Thus, if a particular scanner has n detector rings with an x center-to-center spacing, this will lead to n direct planes and n − 1 cross planes for a total of 2n − 1 planes with a center-to-center spacing of x/2.
Axial sampling of 2D PET and Michelograms. Figure shows multiring PET scanner with 16 rings in axial direction. (A) Coincidence events involving detectors within same ring (e.g., detectors in Ring 3 in coincidence with detectors on opposite side of Ring 3) are referred to as “direct” coincidences. In this figure there are 16 “direct” planes. (B) In many PET scanners, inclusion of “cross” coincidences (e.g., events in Ring 2 allowed to be in coincidence with detectors in Ring 3 and vice versa) improves axial sampling since these cross coincidence planes are considered to be between 2 planes involved. Top of figure shows both direct and cross plane. Bottom of figure shows all of resulting LORs. (C) Michelogram plots those detectors on one side of gantry that are allowed to be in coincidence with detectors on other side of gantry. In this Michelogram, asterisks (*) only along diagonal imply that only direct coincidences are allowed. This leads to 16 planes being acquired. (D) In Michelogram for direct and cross coincidences 2 cells representing Ring 2 in coincidence with Ring 3, and Ring 3 in coincidence with Ring 2 are connected by straight line indicating that data from both of these cells are combined. If scanner is irradiated by uniform source, there will be twice as many counts in cross planes as in direct planes. In this configuration, there will be 16 direct planes and 15 cross planes for total of 31 planes. Thus, inclusion of cross planes increases axial sampling by factor of 2.
The Michelogram is used to illustrate the amount of axial data combined (3). The detector rings on one side of the scanner are plotted on the x-axis, and the detector rings on the opposite side of the scanner are plotted on the y-axis. In PET, detectors in one ring may be allowed to be in coincidence with only certain rings on the opposite side of the scanner. For example, maybe only direct coincidences are allowed, or possibly both direct and cross coincidences. Allowable coincidences are marked by an asterisk in the cell that represents the intersection of the row and the column associated with those particular detector rings. For example, consider the PET scanner in Figure 6A that has 16 detector rings. Figure 6C shows the Michelogram created if only direct coincidences are allowed for a particular scanner. There are asterisks only in the cells along the diagonal. This configuration leads to data acquired into 16 transverse planes with axial sampling equal to the axial width of a detector. Now consider increasing the axial sampling by including cross coincidences as shown in Figure 6B. When data from cells in the Michelogram are combined into a single plane, it is indicated by connecting the 2 cells with a line segment. The Michelogram for a scanner that uses direct and cross coincidences is shown in Figure 6D. This leads to the acquisition of 31 transverse planes (i.e., 2n − 1) with axial sampling equal to half a detector width (i.e., x/2). Note that if the scanner is exposed to a uniform source of activity, the cross planes will contain twice as many counts as a direct plane, since it combines the data from 2 cells in the Michelogram. This is strictly true only if the sensitivity of each cell in the sinogram is equal. There may be small differences in the cell sensitivities due to the presence of the interplane septa. This interplane difference in sensitivity will not be evident in the final reconstructed data because a plane efficiency correction is applied to correct for this effect. However, odd-numbered (direct) planes will be noisier than even-numbered (cross) planes since they contain only half as many counts. The term “span” is used to describe the extent of axial data combined. The span is the sum of the number of cells in the Michelogram combined into an odd-numbered plane added to the number of cells combined into an even-numbered plane. For example, using direct and cross planes as discussed above is a span of “3” because 1 cell is combined into an odd-numbered plane and 2 cells are combined into an even-numbered plane.
The acquisition of direct and cross coincidences provides axial sampling that is equal to half the axial width of the detectors. Many scanners use detectors with small axial widths to provide fine axial sampling. On the other hand, using small detector widths leads to low, in-slice sensitivity and thereby noisy reconstructed images. For this reason, axial data may be combined into a single reconstructed image beyond the direct and cross planes. Consider an odd-numbered plane (excluding the first and last ones, e.g., Plane 3, 5, … 27, or 29) as illustrated in Figure 7A. In addition to the direct plane (e.g., Ring 2 to 2), it also combines the crossed planes on either side of this (Ring 1 to 3, and Ring 3 to 1). The even-numbered planes (excluding the second and second-to-last) not only include the cross planes (Ring 2 to 3, and Ring 3 to 2) but extended cross planes (Ring 1 to 4, and Ring 4 to 1). The axial LORs and Michelogram for this configuration are shown in Figures 7A and 7B, respectively. Since odd- and even-numbered planes combine data from 3 and 4 cells, respectively, this configuration is said to have a span of 7 (i.e., 3 + 4). Note in Figure 7B that the first and last slice still contain only one cell in the Michelogram and that the second and second-to-last have 2 cells combined, whereas the odd- and even-numbered planes thereafter have 3 and 4 cells, respectively. Thus, Planes 1 and 31 have only one third as many counts as the other odd-numbered planes, and Planes 2 and 30 have only half as many counts as other even-numbered planes. In addition, odd-numbered planes (excluding the first and last) have three fourths as many counts as the even-numbered planes. Again, this difference in interplane sensitivity is corrected in the final data by the plane efficiency correction. Figure 7C shows a set of sinograms that were acquired with a span of 7 and have not been corrected for detector or plane efficiency differences. Note that the first and last 2 sinograms in the set have substantially fewer counts than the others. Also note that the even-numbered planes have slightly more counts than the odd-numbered planes. Lastly, note that odd- and even-numbered planes acquired with a span of 7 have 3 and 2 times as many counts, respectively, as the odd- and even-numbered planes acquired with a span of 3. However, combining axial data in this manner leads to only a small loss in axial resolution. For these reasons, some vendors refer to the use of a span of 3 and 7 as “high resolution” and “high sensitivity” modes, respectively.
2D PET with span of 7. (A) Top of figure shows configuration for odd-numbered slices. Not only is direct LOR used but also 2 cross LORs on either side of it. For example, Ring 2 in coincidence with Ring 2, Ring 3 with Ring 1 and Ring 1 with Ring 3. For even-numbered slices, 2 sets of cross LORs are used (e.g., Ring 2 to Ring 3, Ring 3 to Ring 2, as well as Ring 1 to Ring 4, and Ring 4 to Ring 1). Since odd-numbered planes contain 3 LORs and even ones contain 4, this is referred to as span of 7. (B) Michelogram for 16-ring scanner using span of 7. (C) Set of sinograms corresponding to Michelogram in (B) that have not been corrected for detector sensitivity or plane efficiency is shown. Note that first and last 2 sinograms have substantially fewer counts than others and that even-numbered sinograms have slightly more counts than odd-numbered ones.
An alternative method of increasing the number of counts in each sinogram pixel is to combine angular rather than axial samples. In most cases, the size of the detectors within the scanner is selected to achieve the desired transverse spatial resolution, that is the spatial resolution that will be realized in the reconstructed slice. However, using small detectors also increases the number of detectors per ring and thereby the number of angular samples. More angular samples mean more rows in the sinogram and thus more data to be stored. In some cases, the number of angular samples can be reduced without adversely affecting the reconstructed image quality. To reduce the number of angular samples by a factor of 2, one would add every other row in the sinogram to the previous row and assume the resultant data were acquired half way between the 2 samples. This manner of reducing the angular sampling is referred to as “sinogram mashing.” The resultant sinogram would go from approximately 256 rows to 128 rows, and the resultant raw data would only take up half as much disk space. Sinogram mashing is applied in factors of one half, and the “mashing factor” indicates how many such factors have been applied. Thus a mashing factor of 1 reduces the data by a factor of 2, a mashing factor of 2 reduces the data by a factor of 4, and so on.
2D and 3D PET
Even in those cases where data are combined either axially (larger spans) or angularly (sinogram mashing), the resultant data are still acquired in a series of sinograms that represents a set of parallel, 2D transverse planes that can be reconstructed independently of each other. For this reason, these methods of acquiring and reconstructing PET data are referred to collectively as 2D PET. With 2D PET, septa are often placed between the detector rings to reduce the interplane scatter. These septa are thin rings (∼1 mm thick) of lead or tungsten. The outer diameter of the septal rings is equal to the ring diameter of the scanner, and the difference between the inner and outer diameters of the septa varies from 7 to 10 cm, depending on the vendor. A scanner using septa is illustrated in Figure 8. These septa should not be considered “collimators,” as used with a gamma camera, but more like the “antiscatter grids” used in radiography. They do not provide spatial definition but simply reduce the amount of interplane scatter incorporated into the data acquisition. The use of septa reduces the fraction of detected photons that have been scattered from 30%−40% to 10%−15%. Axial data can still be combined when using septa. Data with spans of 7 or 11 may be possible when using septa.
Interplane septa. In many 2D-PET scanners, septa are placed between detector rings to reduce amount of interplane scatter. In modern scanners, one can mechanically retract septa so that scanner can be operated in either 2D or 3D mode.
Retracting the septa allows coincidences from any detector ring with any other detector ring. For example, detectors in the first and last detector rings in the scanner could be in coincidence. The advantage of not using septa is that the sensitivity of the scanner is substantially improved by a factor of between 4 and 6. The disadvantages are the increase in the amount of scatter (from 10%−15% to 30%−40%), the increase in the random coincidences from activity that is out of the field of view, and the necessity of using some form of 3D reconstruction technique. Typically, 3D reconstruction algorithms are substantially more complicated and time consuming than 2D methods. Several methods have been developed for rebinning 3D data such that they can be reconstructed with 2D algorithms (3,7). When PET data are acquired in a manner such that they are NOT inherently organized into a series of parallel 2D-transverse slices, this is referred to as 3D PET (7). Most current scanners with septa have a mechanism for retracting the septa from the field of view, and thus refer to the acquisition of data with and without septa as 2D and 3D modes, respectively. Some older scanners may have fixed septa that only allow data to be acquired in 2D mode. There are also some scanners that do not have septa and thereby can only acquire data in 3D mode.
Even when acquiring in 3D mode, one may limit the range of allowable coincidences. The axial extent of the coincidences allowable in 3D PET is characterized by the “maximum ring difference” (RD). Consider the scanner with 16 detector rings. If all possible coincidences are allowed (i.e., Ring 1 is allowed to be in coincidence with Ring 16), then RD = 16 − 1 = 15. Note that RD defines the maximum ring difference since all rings except Rings 1 and 16 would have possible ring-difference values smaller than this. For example, the highest ring difference for Ring 5 would be 11 (16 – 5). Figure 9A shows the axial LORs for acquiring data with RD = 11. Michelograms for RD = 11 and 15 are shown in Figures 9B and 9C, respectively. The RD = 15 case, leads to 152 or 225 allowable cells in the Michelogram. The orientation of reconstructed transverse planes will be parallel to the direction of the arrow indicated in Figures 9B and 9C. By comparing the number of Michelogram cells along each reconstructed plane, one can see that planes in the center of the gantry have the highest plane sensitivity whereas the planes on the axial periphery have the lowest. In fact, Planes 1, 2, 30, and 31 have the same plane sensitivity as they did in the 2D case. In the RD = 11 case, there is a central plateau over which the plane sensitivity does not drastically change. Figure 10A plots the plane sensitivity for RD = 15 and RD = 11 as a function of axial position or plane number. For comparison, the case of the 2D with span of 7 is also included. In all cases, the plane sensitivity ramps up to a maximum value toward the axial center of the gantry and eventually the ramps down. For RD = 15, the plane sensitivity curve is a triangular function with the maximum in the middle of the gantry. The other 2 cases define trapezoids with a central plateau of maximum sensitivity. 3D PET provides a substantial increase in plane sensitivity, but that increase is limited to the axial center of the gantry. Note that in all 3 cases, the plane sensitivities in the first and last 4 planes are identical. An RD of 11 may be preferable to maintain a central region of uniform sensitivity. If one were to acquire a 2-bed position study in 3D and would like to maintain uniform sensitivity at the bed-position transition, the 2 studies would have to be overlapped a distance equal to half the sloped portion of the plane efficiency curve, as illustrated in Figure 10B. The RD = 15 case leads to 152 or 225 allowable cells in the Michelogram as opposed to 31 in the 2D case. Data in each cell can be represented by a sinogram. In this case, 3D data acquisition can lead to more than 7 times as much data being stored than in the 2D case. Thus another drawback of 3D PET is that it requires substantially more data-storage capacity.
3D PET. In 2D PET, data are organized in individual planes that can be reconstructed independently with 2D algorithm. In modern scanners, one can retract septa, allowing many more LORs to be acquired. Some scanners do not have septa and thereby acquire in 3D mode at all times. In 3D PET, one can define “maximum ring difference” (RD) that is allowed. If RD = 11, then Ring 1 is allowed to be in coincidence with Rings 1−12. (A) Acceptable LORs for RD = 11 are shown. (B) Michelogram for 3D acquisition with RD = 11 is shown. Reconstructed planes would be parallel and oriented as shown. (C) Michelogram for 3D acquisition with RD = 15.
Sensitivity and axial position. (A) Figure shows sensitivity for 16-ring scanner with 3 different data acquisitions: 2D with span of 7, 3D with RD = 11, and 3D with RD = 15. As one moves in from edge of scanner, sensitivity increases to maximum. For RD = 15, it peaks in middle, forming triangular function. For RD = 11, there is central plateau of maximum sensitivity. Note that all 3 acquisitions yield similar sensitivity at edges of axial field of view. (B) If multibed study using 3D, scans should be overlapped as shown here to yield relatively constant sensitivity over extended field of view.
In 3D mode, just as with 2D, several cells within the Michelogram can be combined to increase the counts in each sinogram and also reduce the amount of raw data that needs to be stored. One can characterize a particular 3D data acquisition approach by its span and RD value. If a particular span and RD value are defined, the cells in the Michelogram will divide into a series of segments, as shown in Figure 11A. For example, the acquisition with a span of 7 and RD of 15 can be divided into 5 segments. This configuration reduces the number of sinograms from 225 to 95 and the amount of raw data stored by a factor of 2.4. As discussed previously, the raw data acquired in PET can be presented as either sinograms or projection views. The use of the projection view instead of the sinogram can yield an insight into the 3D data acquisition. Consider an object being imaged in 3D with 5 segments as shown in Figure 11. Within each segment, a complete set of projection views will be acquired. For example, if the scanner acquires 256 angular samples, this would yield 256 projection views. The projections in each segment view the object at a different axial angle. The projections in Segment 0 (Fig. 11B) view the object as if it were acquired straight on, similarly to 2D mode. Segment 1 (Fig. 11C) views the object at an inclined angle, θ, whereas Segment −1 (Fig. 11D) views the object from a declined angle, −θ. Similarly, Segment 2 and −2 (Figs. 11Eand 11F) view the object from inclined and declined angles, 2θ and −2θ, respectively. Thus, each segment provides a complete set of 256 projection views at a certain axial angle. For the example in Figure 11, there would be 5 × 256, or 1280, different projection views. The segments with angled views provide a truncated view of the object. In the 3D Michelogram, these truncated views are demonstrated by the reduced number of slices in the inclined segments. Thus, these truncated views are smaller in the y direction, but the same width in the x direction.
3D acquisition. (A) Michelogram for 3D acquisition with 16-ring scanner using RD = 15 and span of 7. Note that Michelogram is organized into 5 segments. (B−F) LORs are shown for segments 1−5, respectively. Note that axially angled segments yield truncated view of object.
Summary
PET data are inherently acquired differently than single photon nuclear medicine data. To appreciate the nature of the acquired data, it is instructive to understand how the data are acquired, sorted, and processed before reconstruction. PET data can be acquired in either 2D or 3D mode. In 2D mode, the acquired data are organized in a series of parallel slices that can be reconstructed independently. Data for 3D PET must be rebinned to resemble 2D data before reconstruction, or a 3D reconstruction algorithm must be used. The raw data from 2D PET can be organized in either sinograms (one for each slice) or in projection views (one for each projection angle). The noise in the raw data as well as the amount of disk space necessary can be reduced by combining either axial (increasing the “span”) or angular (sinogram mashing) samples. Retracting the interplane septa in a PET scanner to acquire 3D PET data increases the sensitivity by a factor of 4−6 but also increases the scatter fraction from 10%−15% to 30%−40%. The Michelogram is useful to understand how 3D PET scans are acquired. In general, several axially angled views of the object are acquired at each projection angle in 3D PET. The sensitivity in 3D PET is highest in the axial center of the gantry and falls off toward the periphery. In fact, the sensitivity of the first and last few slices of a 3D acquisition is the same as the sensitivity of 2D.
Footnotes
For correspondence or reprints, contact: Frederic H. Fahey, DSc, PET Center, Wake Forest University School of Medicine, Medical Center Blvd, Winston-Salem, NC 27157-1061.
E-mail: ffahey{at}wfubmc.edu.