Abstract
Iterative maximum-likelihood expectation maximization and ordered-subset expectation maximization algorithms are excellent for image reconstruction and usually provide better images than filtered backprojection (FBP). Recently, an FBP algorithm able to incorporate noise weighting during reconstruction was developed. This paper compares the performance of the noise-weighted FBP algorithm and the iterative maximum-likelihood expectation maximization algorithm with Poisson noise–corrupted emission data generated by computer simulations and a SPECT experimental study. The results show comparable performance for these 2 algorithms.
Iterative maximum-likelihood expectation maximization (MLEM) (or its ordered-subset version) is the most widely used iterative image reconstruction algorithm in nuclear medicine (1). Many studies have compared MLEM with analytic filtered backprojection (FBP) (2–5). Except for some parametric imaging studies, the output is usually considered much better for MLEM than for FBP (6,7). One reason for the poor performance of FBP is that information about projection noise is not used during reconstruction.
Many researchers have developed preprocessing methods to denoise the projections before FBP is used for image reconstruction. Recently, a noise-weighted FBP algorithm was introduced (8,9), and this paper compares it with the state-of-the-art MLEM algorithm using Poisson noise–corrupted emission projections.
An expansion domain filtering method (10–12) effectively preprocesses projections before an analytic algorithm is applied for image reconstruction. The preprocessing procedure expands the projections into a set of, for example, Kharhunen–Lohve basis functions. Each Kharhunen–Lohve basis function is analogous to a sine wave, and each Kharhunen–Lohve coefficient is analogous to the Fourier series coefficient or frequency component. The optimum Kharhunen–Lohve domain filtering is analogous to the Fourier domain’s Wiener filtering. The noise model is shift-invariant and frequency-dependent. On the other hand, our proposed noise weighting is projection ray–based, resulting in a shift-variant noise model. The resultant reconstruction does not have a shift-invariant property.
It is well understood that image evaluation and comparison are always task-based and that there is no universal criterion. Algorithm A can be better than algorithm B using one criterion whereas algorithm B can be better than algorithm A using another criterion. If the task is lesion detection, an algorithm that can provide a smooth background and a high-contrast lesion wins (13). Some tasks rely on image variance and bias trade-off (14), and others rely on resolution and signal-to-noise trade-off.
In this paper, we adopt the criterion that the best image is that closest to the true image in the sense of the pixel-by-pixel least-squares error. Since the true image must be known in order to use this criterion, only computer simulations are applicable. It is impractical to use real data for the comparison studies because the true image is unknown. However, we can find a noise-weighted FBP reconstruction that is close to an MLEM reconstruction.
Since the emission data MLEM algorithm is well known, the next section describes only the noise-weighted FBP algorithm.
MATERIALS AND METHODS
Noise-Weighted FBP Algorithm
The noise-weighted FBP algorithm is almost the same as the conventional FBP algorithm except that the ramp filter is regulated by newly proposed window functions. The use of window functions in an FBP algorithm is not new. One popular window function is the rectangular function suggested by Ramachandran and Lakshminarayanan (15). Another popular window is smoother than the rectangular function and was proposed by Shepp and Logan (16). Many other low-pass filters, such as the Hamming window (17), the Hann window (which is the raised cosine function) (18), and the Butterworth window (19), are also widely used. These traditional window functions are shift-invariant. On the other hand, our proposed window function is determined by the noise variance of each projection ray (8,9), as Eq. 1where ω is the frequency variable, w(ray) is a weighting function of the projection ray, and k is the parameter that emulates the iteration number as if in an iterative algorithm. In Equation 1, α > 0 is a small prechosen constant that emulates the step size in an iterative algorithm. The main difference between Equation 1 and the formula given by Zeng and Zamyatin (9) is that their formula is more general and considers Bayesian regularization with a regularization parameter β. If β is set to zero, these 2 formulas are identical.
Eq. 1where ω is the frequency variable, w(ray) is a weighting function of the projection ray, and k is the parameter that emulates the iteration number as if in an iterative algorithm. In Equation 1, α > 0 is a small prechosen constant that emulates the step size in an iterative algorithm. The main difference between Equation 1 and the formula given by Zeng and Zamyatin (9) is that their formula is more general and considers Bayesian regularization with a regularization parameter β. If β is set to zero, these 2 formulas are identical.
For emission data’s Poisson noise model, noise variance can be approximated by the projection value, which is the photon count. If the projection value along a ray is p, then the weighting function w(ray) can be chosen as 1/p or a low-pass filtered version of 1/p. If p = 0, w(ray) can be chosen as 1.
Our strategy to implement the window function Equation 1 is to quantitate the weighting function w(ray) into N (e.g., N = 10) values:  , where pmax is the maximum projection value and n = 1, 2,…, 10. The efficient fast Fourier transform is used. The implementation steps of calculating filtered projection q(t,θ) are given below. Here, θ is the view angle and t is the projection bin coordinate along the detector in a parallel-beam imaging geometry.
, where pmax is the maximum projection value and n = 1, 2,…, 10. The efficient fast Fourier transform is used. The implementation steps of calculating filtered projection q(t,θ) are given below. Here, θ is the view angle and t is the projection bin coordinate along the detector in a parallel-beam imaging geometry.
Before the projection data p(t,θ) are ready to process, we form 10 Fourier domain filter transfer functions 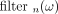 as defined in Equation 2:
as defined in Equation 2: Eq. 2with
Eq. 2with 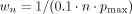 and n = 1, 2,…, 10, respectively. In implementation, ω is a discrete frequency index and takes the discrete values of 0, 1/M, 2/M,…, 1/2, where M is twice the projection array size. If the detector size is 128, then M is 256. When ω = 0, we always define filtern(0) as 0.
and n = 1, 2,…, 10, respectively. In implementation, ω is a discrete frequency index and takes the discrete values of 0, 1/M, 2/M,…, 1/2, where M is twice the projection array size. If the detector size is 128, then M is 256. When ω = 0, we always define filtern(0) as 0.
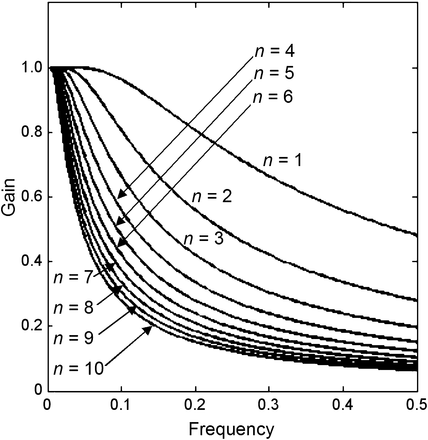
The frequency domain transfer function Equation 2 can be decomposed into the ramp filter |ω| and a window function. For the conventional FBP algorithm, the window function is a constant 1. For the noise-weighted FBP algorithm, the window functions are various low-pass filters as shown in Figures 1–3⇓⇓. Figure 1 shows 10 different window functions, n = 1, 2,..., 10, for k = 6,000. Figure 2 shows 10 different window functions, n = 1, 2,..., 10, for k = 1,868. Figure 3 shows 5 different window functions associated with n = 5 and 5 different k values. The actual implementation steps of the modified ramp filtering are given below:
Step 1: At each view angle θ, find the 1-dimensional Fourier transform of p(t,θ) with respect to t, obtaining P(ω, θ).
Step 2: Form 10 versions of Qn(ω,θ) = P(ω, θ)
 with n = 1,…, 10.
with n = 1,…, 10.Step 3: Take the 1-dimensional inverse Fourier transform of Qn(ω, θ) with respect to ω, obtaining qn(t,θ) with n = 1,…, 10.
Step 4: Construct q(t,θ) by letting q(t,θ) = qn(t,θ) if
 .
.
Window functions (gain vs. frequency) for k = 6,000 and n = 1, 2,…, 10.
Window functions (gain vs. frequency) for k = 1,868 and n = 1, 2,…, 10.
Window functions (gain vs. frequency) for n = 5 and 5 different k values.
A better result can be obtained if p(t,θ) in step 4 is replaced by a low-pass smoothed version of p(t,θ). In this paper, we use a 3-point-avarage filter to smooth p(t,θ) with respect to t and used this smoothed p(t,θ) in step 4 for the purpose of noise-weighting reinstallation. In other words, the weighting function is defined by the smoothed projections. The smoothed projections can be low-pass–filtered heavily or lightly, with respect to one variable or all variables, and they can also be normalized with a maximum value of 1. This smoothed version of p(t,θ) is never used in steps 1–3 for projection data’s ramp filtering and is only used for the design of a noise-weighting function.
In Equations 1 and 2, the parameter α should be chosen such that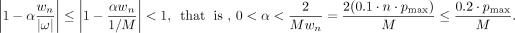 Eq. 3
Eq. 3
We used α = 0.001 for all our computer simulations and real SPECT studies. If one chooses to normalize the smoothed projections in step 4 so that the maximum value is 1, then α can be chosen as any positive value α < 0.2/M. As a matter of fact, in our computer simulations, all projection data are first normalized to a certain maximum value before they are used for image reconstruction. This value is the maximum projection value with the lowest count in a series of noisy phantom studies with the same phantom.
Since the MLEM algorithm has a nonnegativity constraint whereas the FBP algorithm does not have this constraint, after the image is reconstructed with the noise-weighted FBP algorithm all negative-valued pixels are set to zero to have a fair comparison. In fact, there exist better ways to process the negative reconstruction values as suggested by O’Sullivan et al. (20).
Computer Simulations
In this paper, the Poisson noise–weighted FBP algorithm is compared with the iterative MLEM algorithm by using computer simulations. The 2 computer-generated phantoms used in the studies had the same shape and dimension, containing an elliptic torso, the heart, a lung, and background tissues. The radioactivity ratios of heart:background:lung:air were 2.5:1.0:0.25:0 for phantom 1 and 1.75:1.0:0.5:0 for phantom 2.
The projection data were calculated analytically as line integrals of the phantoms (without pixelization of the phantom). Poisson noise was added to the projections; 5 different noise levels and 100 noise realizations for each noise level were used in the simulation studies.
The 1-dimensional detector array contained 128 bins. No scattering, attenuation, distance-dependent blurring, or motion was considered in data generation and reconstruction. The detector stopped at 120 views uniformly distributed over 180°. The images were reconstructed into a 2-dimensional 128 × 128 array using the MLEM algorithm and the noise-weighted FBP algorithm, respectively.
No modification was made to the conventional MLEM algorithm that models the emission Poisson noise. The number of iterations was chosen when the reconstructed image was closest to the true image, that is, when the pixel-by-pixel squared error Eq. 4reached a minimum. The mean squared error (MSE) is calculated for each reconstruction. For each simulation condition, we have 100 noise realizations. The average of the 100 squared errors is reported in the “Results” section as the MSE. In the noise-weighted FBP algorithm, the parameter k was chosen in the same manner, because it emulates the iteration number in an iterative algorithm.
Eq. 4reached a minimum. The mean squared error (MSE) is calculated for each reconstruction. For each simulation condition, we have 100 noise realizations. The average of the 100 squared errors is reported in the “Results” section as the MSE. In the noise-weighted FBP algorithm, the parameter k was chosen in the same manner, because it emulates the iteration number in an iterative algorithm.
In addition to MSE, the bias and SD are also calculated. The definition of the bias is almost the same as that in Equation 4, except that the square is removed. The average of the 100 biases is reported in the “Results” section. The variance is calculated as variance = MSE − (bias)2, and the square root of the variance is the SD.
Phantom Experiment
A Jaszczak torso/heart phantom was filled with 99mTc and scanned with a Siemens Signature SPECT system. Radioactivities in each organ/background (123 MBq [3.3 mCi] in the liver, 30 MBq [0.8 mCi] in the myocardium, and 93 MBq [2.5 mCi] in the background) and scan time (30 min) were similar to those in a routine clinical study. The data acquisition matrix was 128 × 128, and the phantom was scanned using 60 views over 180°. The images were reconstructed into a 128 × 128 array, using the MLEM algorithm and the noise-weighted FBP algorithm, respectively.
Three different numbers of iterations—3, 30, and 3,000—were used in the MLEM reconstructions. The parameter k in the noise-weighted FBP algorithm was chosen according to the minimum of Equation 4, where the true image was replaced by an MLEM reconstruction. In other words, a closest noise-weighted FBP reconstruction was obtained to match the MLEM reconstructions.
RESULTS
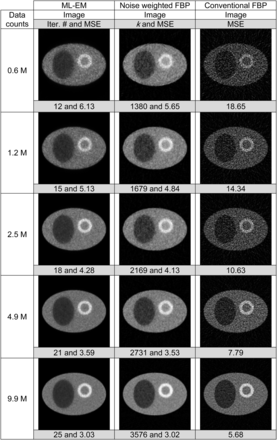
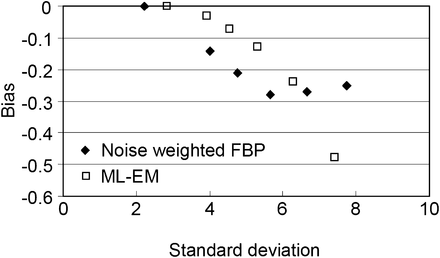
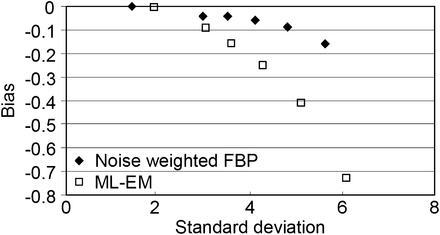
In Figure 4, the optimal MLEM images and the optimal noise-weighted FBP images are compared for phantom 1. The results for phantom 2 are summarized in Figure 5. By optimal, we mean that the images reach the least-squares difference from the true image, that is, the minimum MSE. In Figure 4, phantom 1 results with the MLEM algorithm are better than the noise-weighted FBP results for all noise levels, whereas in Figure 5, phantom 2 results with the MLEM algorithm are not as good as those noise-weighted FBP results for all noise levels. The only difference between phantoms 1 and 2 is the activity ratios for the organs. Phantom 2 has less contrast than phantom 1. This phenomenon suggests that these 2 algorithms exhibit comparable performance. As also shown in Figures 4 and 5, when the noise-weighted FBP algorithm is replaced by the conventional FBP algorithm the performance is dramatically degraded, and this observation implies that the noise weighting in FBP does make a difference. The conventional FBP reconstruction uses the ramp filter, and the window function is a constant 1. The bias-versus-SD curves for phantom studies 1 and 2 are shown in Figures 6 and 7, respectively.
Results of computer simulations using phantom 1.
Results of computer simulations using phantom 2.
Bias vs. SD for computer simulations with phantom 1. From right to left, each dot represents noise level case in Figure 4 from top to bottom. Leftmost dot is for noiseless case.
Bias vs. SD for computer simulations with phantom 2. From right to left, each dot represents noise level case in Figure 5 from top to bottom. Leftmost dot is for noiseless case.
Finally, Figure 8 presents the results of the experimental SPECT study with the torso/heart phantom. Three MLEM reconstructions and 3 corresponding noise-weighted FBP reconstructions are compared. The images from both reconstruction methods are similar, but the MLEM results seem noisier and sharper.
Results of real SPECT torso/heart phantom.
All images are displayed from 0 to the maximum value of each image with a linear gray scale.
DISCUSSION
In our proposed method, every projection ray is assigned to a weighting factor according to its noise variance. This noise weighting is relative from ray to ray and from view to view in the sense that if all weighting factors are scaled by a constant, the algorithm is essentially unchanged. This relative noise weighting emphasizes less-noisy projection rays while deemphasizing noisier rays. This ray-by-ray weighting scheme is different from (i.e., not equivalent to) the view-by-view weighting scheme in which the filter is the same for all projections in the same view.
In this work, we observe another interesting phenomenon: two algorithms are very close in performance. By using the same criterion, algorithm A is better than algorithm B for one object and algorithm B is better than algorithm A for a slightly modified object.
We understand that using the MSE as the figure of merit is problematic in practice and is not meaningful for many tasks (21). This paper merely presents a mathematic case: if the MSE is chosen as the figure of merit, the MLEM algorithm and the noise-weighted FBP can give similar results. Since the FBP algorithm is linear, a potential application of the noise-weighted FBP algorithm is in quantitative imaging—for example, in dynamic studies of compartment modeling.
Why not use one of the many existing window functions (e.g., the Hann window or Butterworth window)? Unlike so many existing window functions, which are specified by the cutoff frequencies, the new window functions are nonstationary and are specifically determined by the data noise.
The iterative MLEM algorithm is an excellent and widely used method for image reconstruction, especially in nuclear medicine imaging. Its projection and backprojection matrices can readily model the imaging geometry, system blurring, photon attenuation, photon scattering, and other effects. On the other hand, it is difficult for an FBP algorithm to model these effects. The distance-dependent blurring can be compensated for by using a postprocessing technique involving further blurring and then deconvolution (22). An FBP algorithm that can compensate for nonuniform attenuation in SPECT is available (23). Unfortunately, this algorithm has poor noise performance. It is interesting to apply the noise-weighting technique to this algorithm to see whether the noise performance can be improved. These open problems will be left for further investigation.
CONCLUSION
This paper suggests that a newly developed noise-weighted FBP algorithm can perform almost as well as the state-of-the-art MLEM algorithm when they are used to reconstruct emission images. The noise-weighted FBP algorithm has a parameter k that emulates the iteration number in an iterative algorithm and must be chosen by the user. The optimal parameters in both algorithms depend not only on the noise level but also on the object. Currently, we do not have a method to determine the parameter k by just looking at the projections.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Footnotes
Published online Oct. 24, 2013.
REFERENCES
- Received for publication June 9, 2013.
- Accepted for publication July 31, 2013.