The Effect of Renal Failure on ¹⁸F-FDG Uptake: A Theoretic Assessment

MATERIALS AND METHODS

The limiting case is defined by theoretic conditions that lead, after an arbitrary ¹⁸F-FDG injected activity, to the highest possible patient radiation dose and the longest possible time to peak tracer activity in the tissue. The first condition (highest possible dose) is fulfilled by assuming that the tracer plasma decay is the tracer physical decay (no biologic decay). The second condition (longest possible time to peak) is fulfilled with the first condition and by assuming that the tracer is trapped irreversibly.

In patients with normal renal function, a 2-compartment model (the blood pool is counted as 1 compartment) has been proposed to quantify the ¹⁸F-FDG uptake rate in tissues, assuming the tracer is trapped irreversibly (1). At the steady state, the rate of trapped tracer change per tissue volume unit dC_T/dt isEq. 1where K is the uptake rate constant, λ is the ¹⁸F physical decay constant (λ = Log2/110 min⁻¹), and C_p(t) is the tracer concentration in the plasma at any time t. For simplicity, let us assume that C_p(t) decays monoexponentially:Eq. 2with α = (Log2)/T_1/2. In patients with normal renal function, T_1/2 involves both the physical and the biologic decay of the tracer. Furthermore, C_p(t = 0) is usually assessed by the ratio of the injected activity to the patient's weight, assuming that the patient's weight is proportional to the patient's volume (C_p(t = 0) ≈ A_inj/W) (7). The solution of Equation 1 isEq. 3

Therefore, the equation of the time–activity curve of trapped ¹⁸F-FDG per tissue volume unit isEq. 4

Furthermore, let us note that dividing Equation 4 by λC_p(t) yields a ratio R, which reflects the tumor-to-background ratio.

In the limiting case, when only the physical decay of the tracer occurs, that is, T_1/2 = 110 min (α = λ), the equation of the time–activity curve of trapped ¹⁸F-FDG per tissue volume unit becomesEq. 5

Furthermore, dividing Equation 5 by λC_p(t) yields a ratio R that is quite simple:Eq. 6

RESULTS

Figure 1 shows the ¹⁸F-FDG blood time–activity curves for T_1/2 = 110 and 37 min, that is, in the limiting case and in patients without renal failure, respectively. The value of 37 min has been derived from α₃ = 0.0125 + 0.0063 min⁻¹ by Hunter et al., when the tracer physical decay is considered (8).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1. 

Theoretic ¹⁸F-FDG blood time–activity curve for T_1/2 = 37 min (patient with normal renal function) (1) and T_1/2 = 110 min (limiting case) (2). Value of λC_p(t = 0) has been arbitrarily set to 1. a.u. = arbitrary unit.

Figure 2 shows theoretic ¹⁸F-FDG tissue time–activity curves from Equation 4 (T_1/2 = 37 min) and Equation 5 (T_1/2 = 110 min). The value of K has been arbitrarily set to 0.05 min⁻¹ (9). The maximal tracer activity in the tissue occurs at about t = 85 and 160 min, for T_1/2 = 37 and 110 min, respectively. At t = 160 min, the value of C_T(t) for T_1/2 = 110 min is 2.3 times greater than that at t = 45 min for T_1/2 = 37 min. At the peak times, the value of C_T(t) for T_1/2 = 110 min is 1.9 times greater than that for T_1/2 = 37 min, respectively. At t = 60 min after ¹⁸F-FDG injection, the value of C_T(t) for T_1/2 = 110 min is 1.4 times greater than that for T_1/2 = 37 min. When a triexponential input function is used (patients with normal renal function), the tracer activity peak is near that obtained with a monoexponential input function (<5 min difference).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2. 

Theoretic ¹⁸F-FDG tissue time–activity curve from Equation 4 for T_1/2 = 37 min (1) and from Equation 5 for T_1/2 = 110 min (2). Values of λC_p(t = 0) and K have been arbitrarily set to 1 and 0.05 min⁻¹, respectively. a.u. = arbitrary unit.

The patient radiation dose depends on T_1/2 by way of the residence time; consequently, for the same amount of injected activity the factor of increase is about 3 (≈110/37) in the limiting case, compared with patients with normal renal function.

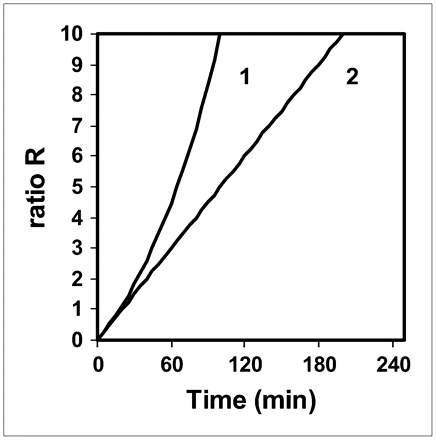
Figure 3 shows the ratio R versus the time delay between injection and acquisition for T_1/2 = 37 and 110 min: R is the ratio of the curves in Figure 2 to those in Figure 1. The values of R for T_1/2 = 37 min in the 45- to 60-min range are similar to those found for T_1/2 = 110 min in the 60- to 90-min range. The value of R for T_1/2 = 37 min at t = 45 min is 2.7 times lower than that for T_1/2 = 110 min at t = 160 min.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 3. 

Ratio R vs. time delay between ¹⁸F-FDG injection and PET acquisition for T_1/2 = 37 min (patient with normal renal function) (1) and T_1/2 = 110 min (limiting case) (2).

DISCUSSION

A 2-compartment model has allowed us to compare the time–activity curve of ¹⁸F-FDG tissue uptake in patients who have normal renal function with that of a theoretic limiting case that leads to the highest possible patient radiation dose (for an arbitrary injected activity) and the longest possible time to peak tracer activity in tissues. The conditions of this limiting case have been arbitrarily set to define extremes for tracer activities to be injected and acquisition times. The condition of the highest possible patient radiation dose is achieved when one assumes that the plasma decay of the tracer is the tracer physical decay. The second condition is fulfilled with the first condition since the tracer plasma decay is the longest one possible, and the second condition also requires the tracer to be trapped irreversibly because the occurrence of a release rate constant can lessen the time to peak tracer activity (2). An anuric patient might fulfill the first condition but would not fulfill the second condition. Indeed, the anuric-patient radiation dose is the highest possible, even if some tracer is taken up in whole-body tissues; however, this last feature is not exactly compatible with the second condition of the proposed framework, that is, the longest possible time to peak tracer activity in tissues (even if the tracer may be partly released back to the blood). Furthermore, the model presented here assumes that, in patients with normal renal function, the ¹⁸F-FDG blood time–activity curve monoexponentially decays after the injection, although it has been shown that the ¹⁸F-FDG plasma clearance was triexponential (8). It is suggested that, in a first approximation, the use of a monoexponential input function in this work may be justified: the third exponential function of a triexponential input function represents the major portion of the whole-blood ¹⁸F-FDG available to the tumor, 89% by Hunter (8); the ¹⁸F-FDG tissue time–activity curves using a tri- or monoexponential input function are similar; and this work emphasizes PET beyond 1 h after the tracer injection, when the third part of a triexponential input function plays the only role.

The comparison of the ¹⁸F-FDG tissue time–activity curve in the limiting case with that of a patient who has normal renal function (Fig. 2) shows that the more severe the renal failure is, the longer is the blood tracer availability to the tissue, the greater is ¹⁸F-FDG tissue uptake, and the later does tracer activity in the tissue maximize (with a limit of 160 min). This reasoning may be extended to the standardized uptake value (SUV) of a tissue, which includes trapped tracer, that is, C_T(t) (Eqs. 4 and 5), and free tracer in the blood and interstitial volumes. Consequently, in patients with renal failure, the tissue SUV should be overestimated (when comparing 2 similar patients with and without renal failure and using similar PET examination parameters). As an example, although free tracer in the blood and interstitial volumes is not considered in the present model, Figure 2 shows that at 60 min after ¹⁸F-FDG injection, the tissue SUV might be about 1.4 times greater in the limiting case than in a patient with normal renal function. However, the tissue SUV should be overestimated in patients with renal failure unless the failure indirectly impairs tissue sensitivity to insulin and hence glucose metabolism (10). Indeed, besides results in various tissues showing an SUV overestimation, Minamimoto et al. reported a small but significant decrease of ¹⁸F-FDG accumulation in the brains of patients with suspected renal failure, compared with healthy volunteers (11). Although the relationship between kidney disease and insulin resistance of the brain is not known, these authors discussed this particular result with the results of other investigators studying diabetes (12,13).

This work presents 2 extremes, that is, normal renal function and a theoretic limiting case, whereas real patients present a spectrum of renal function between these 2 extremes. Therefore, in current clinical practice, this work leads us to propose landmark injected activities and acquisition times for the use of ¹⁸F-FDG PET in patients with renal failure. To obtain a patient radiation dose and tissue ¹⁸F-FDG uptake similar to those of patients without renal failure, and to reduce the dose to the medical staff, we suggest that the injected activity be lowered and that the static PET acquisition be obtained later, depending on the severity of renal failure: the more severe the failure, the lower the injected activity and the later the imaging. Although the model does not allow us to accurately propose what activity should be injected and what imaging timing should be used in a patient with arbitrary renal failure (i.e., between the 2 extremes of normal function and the theoretic limiting case), the model nevertheless suggests that it is not necessary to divide the usually injected activity by a factor of more than 3 or to start the imaging beyond t = 160 min after injection. Indeed, the study of the limiting case shows that to obtain a similar radiation dose to that of patients without renal failure, the injected activity should be divided by a factor of 3 and that one cannot fully compensate for such a lowering factor by performing the acquisition at t = 160 min, since the value of C_T(t) for T_1/2 = 110 min is “only” 2.3 times greater than that at t = 45 min for patients with normal renal function (usual timing in current practice). However, the ratio R, reflecting the tumor-to-background ratio, for T_1/2 = 110 min at t = 160 min is 2.7 times greater than that for T_1/2 = 37 min at t = 45 min.

CONCLUSION

This work shows that ¹⁸F-FDG PET in patients with renal failure can be achieved with an optimized radiation dose, without reducing the tracer tissue uptake: the more severe the renal failure, the lower the injected activity (without exceeding a factor of 3) and the later the imaging (without necessarily beginning the acquisition beyond 160 min after injection). Furthermore, the model also shows that the more severe the renal failure is, the more overestimated is the SUV, unless the renal failure indirectly impairs tissue sensitivity to insulin and hence glucose metabolism.