Abstract
This article discusses CT radiation dose, the measurement of CT dose, and CT image quality. The most commonly used dose descriptor is CT dose index, which represents the dose to a location (e.g., depth) in a scanned volume from a complete series of slices. A weighted average of the CT dose index measured at the center and periphery of dose phantoms provides a convenient single-number estimate of patient dose for a procedure, and this value (or a related indicator that includes the scanned length) is often displayed on the operator's console. CT image quality, as in most imaging, is described in terms of contrast, spatial resolution, image noise, and artifacts. A strength of CT is its ability to visualize structures of low contrast in a subject, a task that is limited primarily by noise and is therefore closely associated with radiation dose: The higher the dose contributing to the image, the less apparent is image noise and the easier it is to perceive low-contrast structures. Spatial resolution is ultimately limited by sampling, but both image noise and resolution are strongly affected by the reconstruction filter. As a result, diagnostically acceptable image quality at acceptable doses of radiation requires appropriately designed clinical protocols, including appropriate kilovolt peaks, amperages, slice thicknesses, and reconstruction filters.
This article, the second in a series of continuing education articles on the principles of CT, focuses first on CT dosimetry and radiation dose and then on CT image quality.
CT DOSIMETRY AND RADIATION DOSE
Before CT came into use, planar radiography and fluoroscopy comprised all non–nuclear medicine uses of ionizing radiation in imaging. In those types of examinations, the radiation dose to the patient maximizes where the x-ray beam enters the surface of the skin. Therefore, it has been reasonable to use radiation exposure to the entry surface (referred to as entrance skin exposure) as an indicator of radiation risk when different techniques, receptors, and x-ray machines are compared. The calculation of entrance skin exposure is straightforward, using measurements of in-air ionization chamber exposure at several x-ray tube kilovoltages covering the clinical range. Such measurements are usually expressed as exposure per milliampere second (mR/mAs, or more properly today, mGy air kerma/mAs).
During scanning of a CT slice, on the other hand, the x-ray beam enters from all directions at some point during the scan. It is no longer clear where (on the surface of or inside the patient) the maximum dose occurs, nor is calculation of the dose at any point in or on the patient straightforward. For example, consider 2 points, A and B, which are, respectively, near the anterior surface and at the center of a cylindric patient. During a 360° rotation, point A receives much radiation when the x-ray tube is above the patient (anterior entry surface). However, point A also receives some (albeit less) radiation when the tube is at every point during its rotation, even when the tube is on the opposite side of the patient. For each tube location, different amounts of radiation reach point A, depending on the depth of A (i.e., how much tissue must be penetrated) and the amount of internal scatter. By comparison, point B inside a symmetric cylindric patient receives the same amount of radiation from all tube locations during the rotation.
Early attempts were made to estimate CT doses by using measurements of dose versus depth summed over all x-ray tube angles and positions. Though commonly used for high-energy beams in radiation therapy, such dose–depth data are too sensitive to differences in x-ray spectra and tissue attenuation to be of value in CT. A different approach was needed: one based on actual measurements inside patient-representative phantoms.
CT Phantoms, Thermoluminescent Dosimeters (TLDs), and CT Dose Profiles
During development of CT dosimetry procedures, 2 standard CT dosimetry phantoms were adopted by the Food and Drug Administration and still are used today (Fig. 1): a 32-cm-diameter cylindric acrylic phantom to represent an adult abdomen, and a 16-cm-diameter version to represent an adult head or small pediatric bodies (1). Both are 15 cm thick (in the z-axis direction) and contain several 1-cm-diameter holes for insertion of dosimeters. The holes are at the center of the phantom and at a 1-cm depth at the 3-, 6-, 9-, and 12-o'clock positions (referred to as the peripheral sites). Some models have holes at other locations at well.
Standard CT dosimetry phantoms consist of cylindric acrylic phantoms with holes for dosimeter insertion at various locations. The 2 sizes are 16 cm in diameter to represent heads and small pediatric bodies and 32 cm in diameter to represent adult bodies. (Courtesy of Lawrence Rothenberg.)
A first step is to understand the nature of the radiation inside the phantom and to investigate the shape of the radiation beam in the z-direction. The z-direction x-ray beam size (the “beam width”) is typically 10 mm or less (usually equivalent to the slice thickness). Because of practical difficulties in using ionization chambers, which were typically larger than the widths of the beams to be measured, TLDs were used for these investigations (1,2).
Each TLD is a small crystal (most commonly lithium fluoride) measuring 3 mm square by 1 mm thick. Special TLD inserts were designed to hold several TLDs, allowing closely spaced x-ray dose measurements within the x-ray beam and more widely spaced measurements outside the beam (Fig. 2). The covered insert would be placed into a phantom hole, and a single scan would be performed with the insert centered in the slice (special alignment inserts were scanned to accurately locate the center of the slice before scanning the TLDs). The exposed TLDs were then read, and the radiation dose for each TLD was plotted against its z-axis position.
Phantom insert to hold TLDs used to measure dose profiles. TLDs are close together within x-ray primary beam and are farther apart to measure profile tails.
An example of such a plot—or single-slice dose profile—for a 10-mm slice thickness is shown in Figure 3. Two observations are of note for this example dose profile: First, the profile width at the levels corresponding to 50% of the peak dose (referred to as the full width at half maximum) is approximately the same as the slice thickness; this observation makes sense in that a wider beam would needlessly expose adjacent tissue, whereas a narrower beam would miss some of the tissue within the slice. Second, a significant level of radiation still is outside the 10-mm-wide slice and deposits some of the dose into adjacent slices. In fact, a measurable amount of the dose (primarily from scatter) may extend several centimeters to either side of the irradiated slice.
Example of doses measured by TLDs inside phantom for a 10-mm slice thickness, plotted as function of TLD position along z-axis. This type of plot is referred to as a dose profile. Slice thickness for single-slice CT scanners is usually equivalent to full width at half maximum of dose profile.
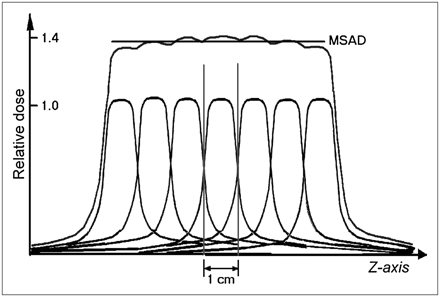
The conclusion is that each slice of tissue receives radiation not only when that slice is scanned but also when adjacent slices are scanned. The exact amounts of additional dose received by a slice from other slices in a series depend on several factors, including scanner geometry, collimator design, slice spacing, and the position of the slice within the series of slices. Axial (nonhelical) examinations generally consist of more than 10 slices with constant spacing. The spacing is usually equal to the slice thickness, in which case the slices are said to be contiguous. Figure 4 provides an example of the cumulative dose from a series of contiguous slices. The average cumulative dose to the central slices from such a series of slices with constant spacing is referred to as the multiple-slice average dose (MSAD). The MSAD may be 1.25–1.4 times the single-slice dose, depending on the factors described above. The cumulative dose to the end slices is somewhat lower than that to the central slices because of a lack of contribution from the one side.
Cumulative dose from a series of contiguous slices is known as multislice average dose (MSAD). Dose-profile tails extend quite far from center of x-ray beam and thus contribute radiation dose to nearby slices. Total dose for a procedure consists of several contiguous slices and is typically 25%–40% higher than single-slice dose.
Practical CT Dosimetry
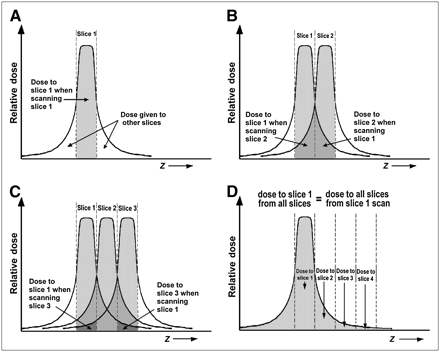
Although informative, routine dose-profile measurements with TLDs are not clinically practical: The measurements are highly time- and labor-intensive, demand careful handling and calibration techniques, and require specialized equipment. Other methods have been used but either also were time- and labor-intensive (film-based techniques) or used devices that were not commercially available (3,4). A practical procedure was needed, and one was soon developed that directly measures a value closely related to MSAD and requires only straightforward ionization chamber measurements (5–7). To understand how such a measurement is made, consider the geometric argument diagrammed in Figure 5.
(A) Dose to slice 1 from scanning of slice 1. (B) Dose to slice 1 from scanning of slice 2 equals dose to slice 2 from scanning of slice 1. (C) Dose to slice 1 from scanning of slice 3 equals dose to slice 3 from scanning of slice 1. (D) Dose to slice 1 from scanning of all slices equals dose to all slices from scanning of slice 1, or total area under dose profile, which is measured using long ionization chamber.
Figure 5A illustrates a single-slice profile when a slice is scanned (which we denote slice 1). The shaded region represents the dose that the tissue of slice 1 receives when slice 1 is actually scanned. As noted, however, the tails of the dose profile also deposit some of the dose in adjacent slices of tissue. Now, suppose we scan a contiguous slice (slice 2) (Fig. 5B). The darker shaded region to the right of slice 1 represents the dose that the scan of slice 1 gives to the tissue of slice 2. Note from symmetry that this dose equals that received by slice 1 when we scan slice 2. We restate this important relationship as follows: The dose that the scanning of slice 1 gives to slice 2 equals the dose that slice 1 gets from the scanning of slice 2.
Continuing in this manner, we scan a third contiguous slice (Fig. 5C). As before, the darkest shaded region to the right represents the dose deposited in slice 3 when slice 1 is scanned, which equals the dose that the scanning of slice 3 gives to slice 1. That is, the dose that the scanning of slice 1 gives to slice 3 equals the dose that slice 1 gets from the scanning of slice 3.
By iterating in this fashion for all slices on both sides of slice 1, we arrive at the following conclusion: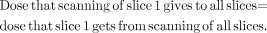
Eq. 1
Now, consider that the dose given by slice 1 to all slices is just the total dose (i.e., the total area) underneath the single-slice dose profile of Figure 5A (redrawn in Fig. 5D to emphasize the entire dose under the curve). Conceptually, it is easy to measure the total dose under the profile: Use an ionization chamber sufficiently long to intercept all dose in the tails of the profile (5,6). A commercially available CT ionization chamber 100 mm in active length is shown in Figure 6 (whether 100 mm is actually long enough to intercept the full profile is discussed in Appendix A). The chamber is inserted into one of the phantom holes and centered in the hole with respect to the z-direction thickness of the phantom, and a single scan is obtained around the center of the phantom. An appropriate f-factor (usually 0.87) and calibration factor are applied to the reading, which is then multiplied by the chamber length and divided by the slice thickness.
Example of 100-mm-long CT ionization chamber for measuring CTDI.
Although a chamber measurement is used to determine the left side of Equation 1, we interpret the result as the right side: that is, as the dose a slice gets from the scanning of all contiguous slices in the series. Such a measurement is called a CT dose index (CTDI). The complete formula, using a chamber of length L, a 0.87 f-factor, and a slice of thickness T, is as follows: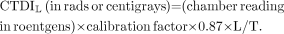
Eq. 2A CTDI obtained using a 100-mm chamber (the most commonly used type) is referred to as a CTDI100. Equation 2 is generalized for multislice CT (to be discussed in the third article of this series) by replacing T in the denominator with N × T, where N is the number of simultaneously acquired slices of thickness T (n = 1 for single-slice CT). Physically, N × T is the total z-direction beam width irradiating the N simultaneous slices. Applying the factor L/T (or L/[N × T] for multislice CT) in Equation 2 is physically equivalent to assuming that the entire radiation dose intercepted by the full chamber length L was actually deposited within the thickness T of the scanned slice. We reiterate the meaning of CTDI: It is the dose (to the phantom location at which it is measured) from a complete series of contiguous slices. When this definition is compared with the definition of MSAD, it seems that CTDI and MSAD are equivalent; in fact, the only practical difference is the length of the dose profile included. Other versions of CTDI (e.g., CTDIideal and CTDIregulatory) also differ only in the length of the dose profile included. These differences are discussed in Appendix A. For our purposes, we will refer to a CTDI measured over a 100-mm profile length (CTDI100), because that is the one most commonly measured.
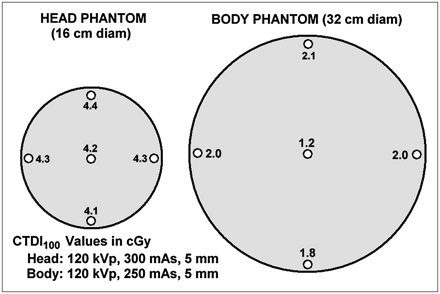
In general, CTDIs measured at different locations and depths in a dosimetry phantom will differ. Figure 7 shows typical CTDIs measured at 120 kVp on a single-slice CT scan of the head and body phantoms with 5-mm collimation (5-mm slice thickness) using clinical technique. Doses for the 4 peripheral (1-cm-deep) holes are nearly uniform, as might be expected from the symmetry of a 360° scan. The CTDI measured at the 6-o'clock position in the body phantom is often somewhat lower because of table attenuation. The CTDI at the center of the head phantom is nearly the same as that at the periphery, whereas the central CTDI in the body phantom is more than half the peripheral CTDI. A high peak kilovoltage (≥120) and symmetric (360°) scans apparently yield doses that vary with depth only moderately in the body phantom and hardly at all in the head phantom. This somewhat counterintuitive result is due to offsetting effects: The dose from primary radiation is higher at the periphery in both cases, but the dose from scatter increases significantly toward the center. Because the long-ionization-chamber measurement includes the tails of the dose profile (which are mostly scatter), CTDIs automatically include both primary and scatter contributions to dose.
Typical central and peripheral doses (CTDI) in head and body phantoms. Central dose is about equal to peripheral dose in head phantom and is more than half the peripheral dose in body phantom. Weighted sum of central and peripheral doses, known as CTDIw, is single-number estimate of patient radiation dose to scanned volume.
In light of the slight-to-moderate variation in CTDI with depth, it is reasonable to ask if there is an average CTDI in the phantom that can be used as a single-number indicator of radiation dose to the patient. A commonly used such indicator is weighted CTDI (CTDIW):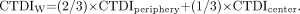
Eq. 3The CTDI measured at the 12-o'clock position is usually used for CTDIperiphery. CTDIW values for the head and body measurements in Figure 7 are 4.3 and 1.8 cGy, respectively. CTDIW, or a related indicator derived from it called CTDIvolume, is often displayed on the CT operator's console during setting of the scan parameters.
CTDI for Noncontiguous Slices and CTDI for Helical Scans
The CTDI defined above and in Appendix A assumes procedures consisting of contiguous slices: that is, slice spacing I equals slice thickness T (or N × T in the case of multislice CT). This is normally the case for axial scans. For helical CT, the parameter analogous to slice spacing is table movement per rotation, which is included in helical pitch, P. Pitch is defined as table movement per rotation I divided by slice thickness T (or more generally as I divided by N × T for multislice CT) (8).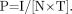
Eq. 4
Because helical scans with P equal to 1 are essentially equivalent to axial scans with contiguous slices, CTDIs for such scans are about the same as for contiguous-slice axial scans using equivalent technique (equivalent peak kilovoltages, amperages, scan times, and slice thicknesses). However, helical CT commonly uses pitches greater than 1 (corresponding to wider spacing between x-ray beams of adjacent rotations) and, in multislice CT, pitches less than 1 (narrower spacing with more overlap of x-ray beams from consecutive rotations).
To account for the effect of pitch on helical dose, and to account for axial scan doses when slice spacing I differs from slice thickness T (or N × T), the indicator CTDIvolume is introduced: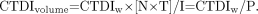
Eq. 5For example, if CTDIw for a helical scan with P equal to 1 is 3 cGy, then the CTDI for the same scan protocol but with P equal to 1.5 would be 3/1.5, or 2 cGy. In effect, CTDIvolume spreads the dose corresponding to CTDIw over a longer (P > 1) or shorter (P < 1) z-axis length of tissue (9).
Dose–Length Products and Effective Dose
A sensible concern about CT radiation dose and risk regards the amount and type of anatomy irradiated. To understand the concern about the amount of irradiated anatomy, consider the following scenario: Mr. Jones undergoes a CT procedure consisting of 20 contiguous slices 5 mm thick (or equivalently, a helical scan 100 mm long with a pitch of 1). Mr. Smith undergoes a scan that is identical except for the number of slices—40 rather than 20 (or an equivalent 200-mm helical scan with a pitch of 1). In each case, the CTDIw measured in the body phantom will be the same (e.g., 3 cGy). Conceptually, however, we believe that Mr. Smith is subjected to greater radiation risk than Mr. Jones, because his radiation burden is double that of Mr. Jones (twice as much tissue received the 3-cGy radiation dose).
CTDI in any form is an estimate of average radiation dose only in the irradiated volume. Risk from ionizing radiation, however, is more closely related to the total amount of the radiation dose (i.e., energy) deposited in the patient. Clearly, Mr. Smith received more total deposited energy than did Mr. Jones. One indicator that is proportional to total deposited energy is the dose–length product, defined as follows: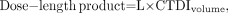
Eq. 6where L is the total z-direction length of the examination. Some CT scanners display dose–length product along with CTDI for each scan. Although proportional to total deposited energy, dose–length product is not in itself an appropriate risk indicator, because dose–length product takes no account of the radiosensitivity of the irradiated tissues. For that purpose, the concept of effective dose (DE) has been introduced (10).
DE is defined as the radiation dose that, if received by the entire body, provides the same radiation risk (i.e., of cancer) as does the higher dose received by the limited part of the body actually exposed (i.e., the scanned volume) (11). Formally, the calculation of DE is complicated: we must estimate the doses deposited in each type of organ and tissue, which then are weighted according to radiosensitivity and summed. The amount of anatomy irradiated and the weighting factors for the tissues involved dramatically affect the resulting DE. The American College of Radiology, as part of its CT accreditation program, uses head and body CTDIw measurements to estimate the effective dose for routine head and abdomen examinations. For head scans, the American College of Radiology assumes a 17.5-cm total scan length and an overall tissue weighting factor of 0.0023. For the abdomen, the scan length and weighting factor are 25 cm and 0.015, respectively. Using the CTDIw values calculated for Figure 7, and assuming contiguous slices (or a pitch of 1), DE for the head and abdomen scans are estimated to be 0.17 and 0.68 cGy, respectively. Although the CTDIw for the head is much higher than that for the body, the abdominal DE is much higher (4 times so) than the head DE, because the head scan irradiates a lesser amount of less radiosensitive tissue (neural tissue and bone).
Once calculated, DE is quite useful: It may be added to the dose the patient received from other x-ray examinations, or it may be compared with radiation doses from naturally occurring sources. Much work is actively under way to develop straightforward methods to estimate effective doses from CTDI measurements (12).
Scanner Design Factors Affecting CT Radiation Dose
Both scanner design factors and clinical protocol factors affect radiation dose to the patient. Some design factors that affect the radiation dose required to achieve a particular image quality have been previously discussed (8). Those are the factors that determine dose efficiency (9).
The ability of a scanner to visualize low-contrast structures is inherently limited by image noise (quantum mottle). For any given radiation dose, maximum sensitivity requires capturing and using as many primary x-rays exiting the patient as possible. Dose efficiency, defined as the fraction of primary x-rays exiting the patient that contribute to the image, has 2 components: geometric efficiency (fraction of transmitted x-rays interacting with active detector areas) and absorption efficiency (fraction of actually-captured x-rays interacting with active detector areas). Geometric efficiency is reduced if some x-rays are absorbed before detection (e.g., in the detector housing) or if some x-rays do not enter active detector areas (e.g., by passing between detectors or striking inactive dividers between individual detectors). Absorption efficiency is reduced if some x-rays that enter the detectors are not absorbed.
Geometric efficiency for modern third-generation single-slice scanners is relatively high (∼80%), with loss being due primarily to dead spaces between detector elements. Geometric efficiency is reduced in multislice CT relative to single-slice CT, because the separations between detector elements in the z-direction create more dead space and because more of the z-direction beam penumbra must be discarded (dose issues in multislice CT will be discussed in the third article of this series). Modern scanners generally use solid-state detectors, with absorption efficiency on the order of 99%.
Other design factors that may affect radiation dose include the distance of the x-ray tube from the isocenter (and thus from the patient), the design of the prepatient x-ray beam collimator, and the design of the bowtie filter and any other beam filtration.
Clinical Scanning Factors Affecting CT Radiation Dose
Radiation dose depends on tube current (amperage), slice scan time, and tube peak kilovoltage. As in radiography, tube current and slice scan time are taken together as mAs in relation to radiation dose and image quality. Increasing the mAs (by increasing tube current or slice scan time) increases the dose proportionally: 300 mAs deliver twice the dose of 150 mAs. Thus, CT radiation dose is often expressed as dose per mAs (or per 100 mAs).
Increasing peak kilovoltage (with all else held constant) also increases radiation dose, because the beam carries more energy. However, increasing peak kilovoltage significantly increases the intensity of the x-rays penetrating the patient to reach the detectors. Therefore, significantly lower mAs are needed to achieve similar image quality. Consequently, a higher peak kilovoltage does not necessarily mean an increased patient dose and, in fact, may allow the dose to be reduced.
CT, slice thickness, slice spacing, and helical pitch may affect dose as well. In single-slice CT with well-designed collimators, dose (as indicated by CTDI) is relatively independent of slice thickness for contiguous slices. Of course, the total length of the area scanned, as well as slice spacing, will determine how much total energy is deposited in the patient. For the same techniques, doses for helical scans with a pitch of 1.0 are equivalent to axial scans with contiguous slices. Pitches greater or less than 1 again affect CTDI values proportionally.
A relatively recent innovation allowing dose reduction in many cases is mA modulation. Before mA modulation came into use, a single mA value was specified (based on experience or the manufacturer recommendation) for the entire scan length, even though patient size or attenuation could change considerably along the scan length (e.g., compare attenuation through the thorax with that through the abdomen for a scan covering both areas). The result was often unnecessarily high mA values (and doses) for some slices, and a perhaps insufficient dose (and reduced image quality) for other slices. Using information from an initial scout view (a low-dose digital radiograph formed from a linear scan as the table moves through the gantry, with the x-ray tube stationary at, for example, 0° or 90°), the scan mA value is individually adjusted, depending on z-position, for each tube rotation. An enhanced version of mA modulation available on some scanners allows a mA adjustment not only for each rotation (z-position) but also as a function of angle during each rotation. Angle-dependent modulation is particularly valuable for anatomic regions in which a patient's anteroposterior and lateral thicknesses are quite different (e.g., the pelvis). In such cases, the preselected mA value is often insufficient to provide adequate x-ray intensity at the detectors for lateral angles or may provide excessive intensity at the detectors for anteroposterior/posteroanterior angles. Angular mA modulation optimizes mA selection for each angle to provide the least radiation dose for the required level of image quality (13).
Summary
CTDIs provide estimates of the radiation dose to the region scanned for the entire series of slices. Although CTDIs are generally much higher for head scans than for body scans, DE for the latter is generally much higher, because more tissue (and more radiosensitive tissue) is irradiated. Furthermore, unlike film/screen radiography, for which narrow ranges of exposure are required to avoid over- or underexposure, CT examinations can be performed with arbitrarily high doses (and the greater the dose, the better the image quality). To help offset trends toward higher doses, the American College of Radiology recommends CTDIW limits of 6 cGy (60 mGy) and 3.5 cGy (35 mGy) for routine head and abdomen scans, respectively. Whether one is considering CTDI or DE, CT radiation doses are considerably higher than the doses from the planar radiography examinations that CT replaced. However, this increase is more than offset by the vastly greater medical information usually provided.
CT IMAGE QUALITY
Fundamentally, image quality in CT, as in all medical imaging, depends on 4 basic factors: image contrast, spatial resolution, image noise, and artifacts. Depending on the diagnostic task, these factors interact to determine sensitivity (the ability to perceive low-contrast structures) and the visibility of details.
CT Image Contrast
CT image contrast depends on subject contrast and display contrast. Because CT display contrast is arbitrary (depending only on the window level and width selected), it will not be discussed further.
As in radiography, CT subject contrast is determined by differential attenuation: that is, differences in x-ray attenuation by absorption or scattering in different types of tissue and thus resulting in differences in the intensity of the x-rays ultimately reaching the detectors. Because of the high peak kilovoltage and relatively high beam filtration (beam hardness) used in CT, the x-ray/tissue interactions (except in bone) are overwhelmingly Compton-scattering events. Differential attenuation for Compton scatter arises from differences in tissue electron density (electrons/cm3), which in turn are due primarily to differences in physical density (14). Thus, subject soft-tissue contrast in CT comes mainly from differences in physical density. That the small differences in soft-tissue density can be visualized on CT is due to the nature of the image (a 2-dimensional image of a 2-dimensional slice), the ability to map small attenuation differences to large differences in gray level by windowing, the near-complete elimination of scatter, and the use of a sufficient x-ray intensity.
Related to CT image contrast is the CT contrast scale. We recall that CT numbers are derived from voxel attenuation coefficients calculated during image reconstruction using the following relationship: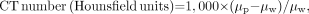
Eq. 7where μp and μw are linear attenuation coefficients for a given voxel and for water (μw is determined from calibration scans). Because CT number is a linear function of μp, a graph of expected CT numbers for materials with known attenuation coefficients should be linear over the clinical CT-number range (e.g., −1,000 to +1,000). For evaluation of the contrast scale of a scanner, various CT test phantoms are available that contain materials designed to provide certain CT numbers (e.g., the CT numbers for water, fat, soft tissue, bone, and air) (15).
CT Spatial Resolution and Sampling
Spatial resolution in CT, as in other modalities, is the ability to distinguish small, closely spaced objects on an image. A common test is an evaluation of limiting resolution, performed using line-pair test patterns. CT phantom line-pair patterns consist of bars of acrylic (or some denser plastic) separated by spaces containing a material that is less attenuating. The widths of the bars and spaces are equal and typically range from about 0.05 or smaller to 0.5 cm. Examples are shown in Figure 8. Bars of lead or other dense materials would cause severe artifacts on CT images and thus are not used. Resolving a line-pair test pattern requires that each bar and space be separately visible on the image. Each bar plus adjacent space is referred to as a line-pair. Rather than specifying bar width, bar pattern sizes are usually described by a spatial frequency in line-pairs per centimeter, defined as follows, where bar width is in centimeters: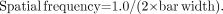
Eq. 8For example, a pattern with 0.1-cm bars and spaces has a spatial frequency of 1/(2 × 0.1), or 5 line-pairs per centimeter. In radiographic imaging, the x-ray tube focal-spot size and blur occurring in the image receptor are the primary causes of reduced resolution. Although focal-spot size does affect CT spatial resolution, CT resolution is generally limited by the size of the detector measurements (referred to as the aperture size) and by the spacing of detector measurements used to reconstruct the image. This concept, called sampling, is illustrated in Figure 9. In Figure 9A, consider a scan of a phantom containing a hypothetical test pattern: for example, 5 line-pairs per centimeter (0.1-cm bars) and detectors that are twice as wide (say, 0.2 cm and spaced by 0.2 mm). The aperture is approximately equal to the detector width—a width that in this case is clearly too large to resolve the smaller bars: All measurements (shown at the bottom of the figure as view data) include attenuation corresponding to half bar and half space. Suppose, instead, that the detector size is reduced to the size of the bars but the spacing is kept at 0.2 cm (5 samples per centimeter; Fig. 9B). Now, even though the aperture is sufficiently small, the bars still are not resolved because the samples are too far apart (in this case, the spaces between bars are missed). In addition to a small aperture, closely spaced measurements are required for good resolution (Fig. 9C). The general rule, known as the Nyquist criterion, states that resolving N line-pairs per centimeter requires measuring at least 2 × N samples per centimeter. For example, resolving 5 line-pairs per centimeter (0.010-cm bars) requires at least 10 measurements per centimeter. Some factors of scanner design associated with sampling were discussed earlier (8).
CT spatial resolution phantom, consisting of 4–12 line-pairs per centimeter (from American College of Radiology accreditation phantom), reconstructed using standard (A) and bone (B, high-resolution) filters.
CT resolution is limited by sampling—size and spacing of measurements (samples) used to form image. (A) Pattern is unresolved because sample size (aperture) is too large. (B) Pattern is unresolved because samples are too far apart. (C) Aperture size and sample spacing are adequate to resolve pattern. (D) “Effective” resolution may be lower than expected because of position of samples relative to pattern. (E) In aliasing, pattern seems to be resolved but with incorrect number of bars.
Two additional sampling-related issues are effective resolution and aliasing. The Nyquist criterion does not guarantee that a pattern will be resolved. For example, suppose that we take the arrangement of Fig. 9C but shift the detectors relative to the pattern (Fig. 9D). Once again, because of an unfortunate alignment of test object and samples causing each measurement to overlap both bar and space, the bars are not resolved. The implication is that a measurement of limiting resolution (using a line-pair test) will in general be lower than what one might expect on the basis of aperture size and sample spacing. This effective resolution is analogous to the Kell factor associated with the vertical resolution of a television screen.
Aliasing is illustrated Figure 9E. Although the bar pattern is too small to be resolved by the size and spacing of the detectors, the view data exhibit a sequence of higher and lower attenuations. However, the view data exhibit fewer highs and lows (bars and spaces) than are actually in the pattern. The image may exhibit bars and spaces that are separate but fewer than those actually in the test object. Such an image is said to be aliased: Because of insufficient sampling, the higher-spatial-frequency test pattern appears in the alias of a lower-frequency pattern and thus is not truly resolved.
Other CT Factors Affecting Spatial Resolution
Focal-spot size does affect CT resolution but to a lesser extent than in radiography. Motion can also introduce blurring, although the more important effect of motion is the potential creation of artifacts. Two additional factors—one potential and one common—are matrix size and reconstruction filter.
The displayed spatial resolution may be affected by reconstruction or by display pixels that are too large. A fundamental limitation is the size and spacing of detector measurements. Suppose that it ought to be possible, on the basis of sampling, to resolve 10 line-pairs per centimeter (0.05-cm bars). Now suppose that a 512 × 512 pixel matrix is reconstructed representing a 50-cm scan circle (i.e., the image represents a 50-cm-diameter area, which might be the case for a scan of a large body). The size of the pixels is approximately 0.1 × 0.1 cm (i.e., 50 cm/512 pixels), which is too large to resolve the 0.05-cm bars. It is often possible, if raw data are not yet overwritten, to reconstruct an image over a smaller circle, say 25 cm, to yield smaller pixels and higher resolution. Similarly, if the display pixels are larger than the reconstruction matrix pixels (uncommon in modern scanners), full resolution will not be displayed. If so, a graphic zoom (a function available on most scanners) will provide better resolution.
Although pixel size may affect resolution (e.g., for large scan circles), a reconstruction filter always affects resolution—often dramatically. A reconstruction filter is applied during filtered backprojection reconstruction to remove the blur from images (8). Usually, however, the filter is deliberately chosen to produce somewhat blurry images. The reason is that overly sharp CT images are usually too corrupted by image noise for most diagnostic tasks. A blurry filter also blurs noise and thus produces better diagnostic quality. For imaging tasks requiring more detail (e.g., to view bone), the operator may optionally select a sharper filter when setting the parameters for the scan. Commonly used filters are designed as compromises between acceptable spatial resolution and an acceptable level of noise. For example, a standard filter may produce images with a maximum resolution of, say, 6 line-pairs per centimeter, whereas a bone filter may image with a resolution of 10 line-pairs per millimeter or better. The test phantom is shown reconstructed with both a standard filter (Fig. 8A) and a high-resolution (bone) filter (Fig. 8B).
Image Noise
If a graphic cursor is used to display pixel CT numbers in an image of a uniform phantom (e.g., a phantom containing all water), it is seen that the CT numbers are not uniform but rather fluctuate around an average value (which should be approximately 0 for water): Some pixels are 0, some are +1, some +2, some −1, and so forth. These random fluctuations in the CT number of otherwise uniform materials appear as graininess on CT images. This graininess is the CT analog of—and is of the same nature as—radiographic quantum mottle: It is due to the use of a limited number of photons to form the image (16,17).
In radiography, image noise is related to the numbers of x-ray photons contributing to each small area of the image (e.g., to each pixel of a direct digital radiograph). In CT, x-rays contribute to detector measurements and not to individual pixels. CT image noise is thus associated with the number of x-rays contributing to each detector measurement. To understand how CT technique affects noise, one should imagine how each factor in the technique affects the number of detected x-rays. Examples are as follows:
X-ray tube amperage: Changing the mA value changes the beam intensity—and thus the number of x-rays—proportionally. For example, doubling the mA value will double the beam intensity and the number of x-rays detected by each measurement.
Scan (rotation) time: Changing the scan time changes the duration of each measurement—and thus the number of detected x-rays—proportionally. Because amperage and scan time similarly affect noise and patient dose, they are usually considered together as mA × s, or mAs.
Slice thickness: Changing the thickness changes the beam width entering each detector—and thus the number of detected x-rays—approximately proportionally. For example, compared with a slice thickness of 5 mm, a thickness of 10 mm approximately doubles the number of x-rays entering each detector.
Peak kilovoltage: Increasing the peak kilovoltage increases the number of x-rays penetrating the patient and reaching the detectors. Thus, increasing the kilovoltage reduces image noise but can (slightly) reduce subject contrast as well.
Although not affecting the numbers of detected x-rays, a reconstruction filter profoundly affects the appearance of noise in the image: Smooth filters blur the noise, reducing its visual impact, whereas sharp filters enhance the noise. In images of soft tissue, noise is generally more interfering than blur, and smoother filters are preferred. In images of structures with edges and small details, such as bone, blur is generally more interfering than noise, and sharper filters are preferred. For comparison, Figure 10 shows examples of noise in scans of uniform phantoms using standard and higher-resolution (bone) filters and with standard and very low values for mAs.
CT image noise depends on number of x-ray photons contributing to image. (A and B) Comparison of noise from scans using 270 mAs (typical clinical value) and 100 mAs. (C) Appearance of image noise is strongly affected by reconstruction filter; sharp filter such as bone also sharpens (enhances) appearance of noise.
Because CT noise appears as fluctuations in CT numbers, a measurement of image noise is a measurement of these fluctuations, and such a measurement can be made using regions of interest (ROIs) on a scan of a uniform phantom. A statistical ROI function (available on most CT scanners) allows users to place a rectangular or oval ROI on the image, within which is calculated the average and standard deviation (SD) of the CT numbers for the enclosed pixels. The SD indicates the magnitude of random fluctuations in the CT number and thus is related to noise: The larger the SD, the higher the image noise. A more complete discussion of image noise is presented in Appendix B.
Because noise is the most bothersome when one is viewing low-contrast soft-tissue structures, an important test of scanner performance is how well low-contrast test objects are seen in the presence of typical noise levels. Figure 11 is an example of a low-contrast test phantom, consisting of groups of rods embedded in material producing approximately 0.6% subject contrast (i.e., a nominal CT-number difference of 6 between the rods and the background). The rod groups range in diameter from 6 to 2 mm. In this example, the 5-mm rods are visible, whereas the smaller ones are lost in the noise.
Low-contrast phantom to test CT performance in presence of typical image noise levels (from American College of Radiology accreditation phantom). Five-millimeter rods are visible, but smaller ones are obscured by noise.
Image Artifacts
Artifacts may be defined as any structure that is seen on an image but is not representative of the actual anatomy. Most types of CT artifacts fall into 1 of 3 categories: shading artifacts, ring artifacts, or streak artifacts (18).
The most common type of shading artifact is beam-hardening effects. Beam-hardening artifacts are actually present on all CT images to some extent and are due to imperfect beam-hardening correction. They appear as nonuniformities in the CT numbers of a uniform material, such as CT numbers that are lower at the center of a uniform phantom than at the periphery. Such nonuniformities are generally quite small (<5 HU) and not apparent unless one is viewing a scan of a uniform phantom with a very narrow window. Occasionally, however, a larger amount of hardening occurs when the scan is passing through thick regions of bone or through contrast medium. In that case, regions of hypointensity (i.e., CT numbers that are lower than expected) may appear downstream along the paths of rays that have been overly hardened (Fig. 12). Scatter can also cause shading artifacts, although these are uncommon in most modern scanners.
Beam-hardening artifact caused by unusually severe hardening of x-rays passing though thick bone.
Ring or partial ring (arc) artifacts are associated with third-generation scan geometry and were discussed previously (8). Ring artifacts arise from errors, imbalances, calibration drifts, or other measurement inaccuracies in an element of a detector array relative to its neighbors. Each detector in a third-generation scanner always measures rays passing at a fixed distance d from the center of rotation, with d depending on the location of the detector within the array. Any such inaccuracies in measurements from a particular detector occurring during a scan (or part of a scan) are backprojected along the ray paths measured by that detector. These inaccuracies contribute only slightly to pixels over most of the image (because several hundred backprojected values contribute to each pixel) but tend to reinforce along a ring of radius d, where several such rays intersect.
Ring (or arc, if occurring during only part of the scan) artifacts are usually readily recognizable by software ring-correction algorithms and thus can be removed from the image. Small-radius rings (i.e., near the center of rotation) or arcs of small angular extent may not be recognized as artifacts and thus wind up in the image. In practice, third-generation scanners are sensitive to detector inaccuracies, which, without corrective algorithms, would be visible on most or all CT images.
Streak artifacts may occur in all scanners. Although arising for many reasons, most are due to inconsistent or bad detector measurements. Factors causing inconsistencies include motion (anatomy in different locations during different parts of the scan), partial-volume effects, metal (a measured intensity that is under the calibrated range of the detector, and possibly beam-hardening and partial-volume effects), insufficient x-ray intensity (leading to high random errors), and malfunctions (tube arcing or system misalignment). An inconsistency due to partial-volume effects is illustrated in Figure 13. During a 360° axial scan, the same ray (or nearly the same ray) is sampled twice, but with x-rays traveling in opposite directions. Because of beam divergence, however, the cone-shaped x-ray beam samples slightly different volumes in each direction. A small structure, such as the edge of a bone, may partially extend into the volume so as to attenuate the beam traveling in one direction (say, downward when the tube is above) but may be missed when the beam is coming from the opposite direction (upward, when the tube is underneath). The 2 measurements of the same ray path are thus inconsistent and will lead to an image streak.
Partial-volume streaks are caused by opposing x-ray beams, which nominally pass through the same voxels but actually sample slightly different cone-shaped tissue volumes as a result of beam divergence. Small structure, such as piece of bone, is detected by beam from one direction but is missed by opposing beam. Resulting inconsistency leads to streak artifact.
Regardless of the source, the effect of an inconsistency is the creation of a streak artifact because of the nature of backprojection reconstruction. In some cases, inconsistencies can be recognized and corrected by software algorithms. In other cases, streaks may be avoided or minimized through appropriate scan techniques, including scanning past 360°, known as overscanning (to reduce streaks due to some motion), or using thinner slices (to minimize partial-volume effects).
CONCLUSION
This article has discussed CT radiation dose, the measurement of CT dose, and CT image quality. The most commonly used dose descriptor is CTDI, which represents the dose to a location (e.g., depth) in a scanned volume from a complete series of slices. A weighted average of the CTDI measured at the center and periphery of dose phantoms, CTDIw, provides a convenient single-number estimate of patient dose for a procedure, and this value (or a related indicator that includes the scanned length, CTDIvolume) is often displayed on the operator's console.
CT image quality, as in most imaging, is described in terms of contrast, spatial resolution, image noise, and artifacts. A strength of CT is its ability to visualize structures of low contrast in a subject, a task that is limited primarily by noise and is therefore closely associated with radiation dose: The higher the dose contributing to the image, the less apparent is image noise and the easier it is to perceive low-contrast structures. Spatial resolution is ultimately limited by sampling, but both image noise and resolution are strongly affected by the reconstruction filter.
As a result, diagnostically acceptable image quality at acceptable doses of radiation requires appropriately designed clinical protocols, including appropriate kilovolt peaks, amperages, slice thicknesses, and reconstruction filters.
APPENDIX A
MSAD and Various Forms of CTDI
The dose indicators MSAD and CTDI represent dose to a particular location in a dosimetry phantom from a complete series of slices. The only practical difference between MSAD and various forms of CTDI is the length of the dose profile included. By definition, MSAD is the dose from all slices in a particular procedure, however many slices are done and however long the z-axis length covered by the procedure. The various forms of CTDI, on the other hand, refer to specific lengths of a dose profile included in the measurement. Ideally, the measured dose profile length should include the entire significant length of the profile, which we denote as CTDIideal. However, because the profile may extend far toward either side of the scanned slice, CTDIideal is difficult to measure in practice.
For regulatory purposes, the Food and Drug Administration defines CTDI as the measurement over a profile length corresponding to a specific number of contiguous slices (14 slices). This quantity, called CTDIregulatory, must be reported by manufacturers in sales literature. This definition creates difficulty for thin slices: For example, a 3-mm thickness requires a CTDI measured over a length of 14 × 3, or 42 mm. Because the dose profile may be (and generally is) quite significant beyond those limits, CTDIregulatory may significantly underestimate the dose for procedures consisting of more than 14 slices (usually the case for thin slices).
For practical purposes, a CTDI measured over 100 mm (the length of most commercially available CT ionization chambers) is the quantity reported by physicists and others who routinely measure CT dose in the field (including Food and Drug Administration inspectors). Because CT scans generally cover at least 100 mm, and assuming the dose profile tails beyond the 100-mm chamber length are minimal, the CTDI100 provides a useful estimate of patient dose in the scanned area for typical CT procedures. In reality, however, the profile may be significant well beyond the limits of the 100-mm chamber. In this case, CTDI100 misses significant fractions of the profile and thus underestimates the actual MSAD (perhaps significantly). These issues and associated solutions are still under investigation and discussion.
APPENDIX B
CT Image Noise
For a well-designed CT scanner, image noise (quantum mottle) should be statistical: that is, due to random variations in detected x-ray intensity (electronic and other noise sources should be minimal in comparison). Quantitatively, these statistical fluctuations are described by the Poisson distribution, which states that the size of random variations (referred to as the SD) associated with measuring N x-rays is given by the square root of N. For example, if we detect 10,000 x-rays and then repeat this measurement several times, the measurements will not be exactly 10,000 each time but will fluctuate around an average or mean value of 10,000. The size of the random fluctuations will be on the order of 100 (the square root of 10,000). We would thus say that our measurement was 10,000 ± 100.
Normally, these random fluctuations are expressed as a coefficient of variation, which for the Poisson distribution is 1/(square root of N). This expression tells us that increasing N (by increasing the dose) reduces the size of the random variations and thus the amount of noise. The square root relationship means that reducing noise (i.e., the size of the fluctuations) by half requires using 4 times as much radiation dose to the slice (by some combination of increased mAs, thicker slices, or other factors).
An estimate of CT-number fluctuations within a small area of an image of uniform material is provided by the SD calculated using a graphic ROI function. A way to verify that image noise is due to limited numbers of x-rays (and not to contamination by other sources) is to graph ROI measurements made at the same location on images obtained using different doses (e.g., using a range of mA values from low to high) versus the inverse square of the dose. The result for a quantum-limited system should be a straight line through the origin.
Footnotes
-
↵* NOTE: FOR CE CREDIT, YOU CAN ACCESS THIS ACTIVITY THROUGH THE SNM WEB SITE (http://www.snm.org/ce_online) THROUGH DECEMBER 2009.
-
COPYRIGHT © 2007 by the Society of Nuclear Medicine, Inc.
References
- Received for publication November 10, 2006.
- Accepted for publication May 15, 2007.
Jump to section
Related Articles
Cited By...
- Optimizing Contrast Resolution in Digital Chest Radiography by Varying Copper Filtration and kVp
- Assessment of Image Quality in Chest CT With Precision Matrix and Increased Framing Rate Using Single Source CT: A Phantom Study
- Micro-CT analyses of the lung in mice: Parameters influencing the radiation dose and acquisition quality
- Radiation Protection in Computed Tomography
- A comparative evaluation of cone beam CT and micro-CT on trabecular bone structures in the human mandible
- Influence of cone beam CT scanning parameters on grey value measurements at an implant site
- Influence of scan setting selections on root canal visibility with cone beam CT
- Adult patient radiation doses from non-cardiac CT examinations: a review of published results
- Assessment of Patient Exposure to X-Radiation from SPECT/CT Scanners
- Principles of CT: Multislice CT