Research ArticleContinuing Education

The MIRD Schema for Radiopharmaceutical Dosimetry: A Review

Pat Zanzonico
Journal of Nuclear Medicine Technology June 2024, 52 (2) 74-85; DOI: https://doi.org/10.2967/jnmt.123.265668

Abstract

Internal dosimetry evaluates the amount and spatial and temporal distributions of radiation energy deposited in tissue from radionuclides within the body. Historically, nuclear medicine had been largely a diagnostic specialty, and the implicitly performed risk–benefit analyses have been straightforward, with relatively low administered activities yielding important diagnostic information whose benefit far outweighs any potential risk associated with the attendant normal-tissue radiation doses. Although dose estimates based on anatomic models and population-average kinetics in this setting may deviate rather significantly from the actual normal-organ doses for individual patients, the large benefit-to-risk ratios are very forgiving of any such inaccuracies. It is in this context that the MIRD schema was originally developed and has been largely applied. The MIRD schema, created and maintained by the MIRD committee of the Society of Nuclear Medicine and Molecular Imaging, comprises the notation, terminology, mathematic formulas, and reference data for calculating tissue radiation doses from radiopharmaceuticals administered to patients. However, with the ongoing development of new radiopharmaceuticals and the increasing therapeutic application of such agents, internal dosimetry in nuclear medicine and the MIRD schema continue to evolve—from population-average and organ-level to patient-specific and suborgan to voxel-level to cell-level dose estimation. This article will review the basic MIRD schema, relevant quantities and units, reference anatomic models, and its adaptation to small-scale and patient-specific dosimetry.

Internal dosimetry evaluates the amount and spatial and temporal distributions of radiation energy deposited in tissue from radionuclides within the body. It has been applied to the determination of tissue-absorbed doses and related quantities for occupational exposures in radiation protection, environmental exposures in radiation epidemiology, and diagnostic and therapeutic radiopharmaceuticals in nuclear medicine. For diagnostic radiopharmaceuticals, dosimetry is generally based on reference, or standard, anatomic models and average human or, oftentimes, animal kinetic (i.e., time–activity) data. Historically, nuclear medicine had been largely a diagnostic specialty, and the associated risk–benefit analyses implicitly performed by the clinician have been straightforward: relatively low administered activities yield important diagnostic information whose benefit far outweighs any potential risk associated with the attendant normal-tissue radiation doses. Although the dose estimates based on anatomic models and population-average kinetics may deviate rather significantly from the actual normal-organ doses for individual patients, the large benefit-to-risk ratios for diagnostic nuclear medicine are very forgiving of any such inaccuracies. Such dose estimates are nonetheless useful for first-order assessment of the relatively low stochastic risk (probability of harm) associated with diagnostic agents as well as for dosimetric intercomparison of different radiopharmaceuticals and imaging procedures and methodologic refinement of such procedures to minimize patient doses. It is in this context that the MIRD schema was originally developed and has been largely applied. The MIRD schema refers, of course, to the formalism created and maintained by the MIRD committee of the Society of Nuclear Medicine and Molecular Imaging; it comprises the notation, terminology, mathematic formulas, and reference data for calculating tissue radiation doses from radiopharmaceuticals administered to patients (1–3).

By incorporation of appropriate radionuclides and appropriately large activities into target tissue–avid radiopharmaceuticals, a sufficiently high radiation dose may be delivered to produce a therapeutic response in tumor or other target tissue. With escalating administered activities and associated normal-tissue doses, serious radiation injury can ensue, however. To optimize radiopharmaceutical therapy, it is critical to establish patient-specific target-tissue and at-risk normal-tissue radiation doses with reasonable accuracy and precision and to develop and apply reliable dose–response relationships for target tissues and dose–toxicity relationships for normal tissues. With the ongoing development of new radiopharmaceuticals and the increasing therapeutic application of such agents, internal dosimetry in nuclear medicine and the MIRD schema continue to evolve—from population-average and organ-level to patient-specific and localized (or voxel-level) dose estimation (3,4).

This article will review the basic MIRD schema, relevant quantities and units, reference anatomic models, and, briefly, its adaptation to patient-specific dosimetry in the setting of radiopharmaceutical therapy. Multiple-choice questions and answers, with detailed explanations of the correct answers, are provided. Radiopharmaceutical absorbed doses and related dose metrics are determined largely by calculation, rather than by direct measurement, and internal dosimetry is, to some extent, unavoidably mathematic. However, the mathematics used are essentially arithmetic, and knowledge of calculus and other advanced topics is not required to read and understand this article.

QUANTITIES AND UNITS

Before addressing the computational engine of the MIRD schema—the actual dose-calculation formulas—one should first be conversant with its language, that is, the quantities, parameters, and symbols that populate the schema. These are detailed in Table 1. For completeness, additional important quantities encountered in radiation dosimetry (5–8) are presented next.

View this table:
TABLE 1.

Terminology and Nomenclature Used in MIRD Schema (1–3)

Absorbed Dose

Perhaps the most widely used and biologically meaningful quantity for expressing radiation dose, the absorbed dose, D, is defined as follows: Embedded ImageEq. 1 where Embedded Image is the mean energy imparted by ionizing radiation to matter and dm is the mass of matter to which the energy is imparted. The SI unit of absorbed dose is the gray (1 Gy = 1 J kg−1), and the older unit is the rad (1 rad = 100 erg g−1); 1 Gy equals 100 rad and 1 rad equals 1 cGy (or 10 mGy).

Linear Energy Transfer

The quality as well as the quantity of radiation are important determinants of the frequency or severity of radiogenic biological effects. The quality of a radiation is related to the characteristics of the microscopic spatial distribution of energy-deposition events. Sparsely ionizing radiations such as x- and γ-rays and intermediate- to high-energy electrons and β-particles are characterized as low-quality radiations, whereas densely ionizing radiations such as low-energy electrons (e.g., Auger electrons), protons, neutrons, and α-particles are typically characterized as high-quality radiations. For the same absorbed dose, the probability or severity of biological effects is generally less for sparsely ionizing than for densely ionizing radiations.

The quality of radiation is characterized by the linear energy transfer: Embedded ImageEq. 2 where dE is the energy deposited by a charged particle (or the secondary charged particle produced by the primary radiation) over a pathlength dl traversed in matter. The SI unit of linear energy transfer is the J m−1, and the older unit is the keV μm−1; 1 J m−1 equals 6.25 × 109 keV μm−1 and 1 keV μm−1 equals 1.60 × 10−10 J m−1. In practice, linear-energy-transfer values are most commonly expressed in the older unit of keV μm−1.

Relative Biological Effectiveness

The influence of linear energy transfer and other radiation properties on the probability or severity of biological effects is quantified by the relative biological effectiveness: Embedded ImageEq. 3 where Dreference is the absorbed dose of reference radiation (typically a widely available sparsely ionizing radiation such as 60Co γ-rays) required to produce a specific, quantitatively expressed biological effect under specific irradiation conditions and DA is the absorbed dose of radiation A (i.e., the radiation for which the relative biological effectiveness is being determined) required to produce the same probability or severity of the same specific biological effect under the same conditions as those for the reference-radiation irradiation.

Equivalent Dose

An important dosimetric quantity, defined by the International Commission on Radiological Protection (ICRP) and used in radiation protection, is the equivalent dose, which is derived from the absorbed dose. Specifically, equivalent dose is the product of an organ- or tissue-absorbed dose and a radiation weighting factor (wR), which ranges from unity for sparsely ionizing radiations such as x- and γ-rays and β-particles to 20 for densely ionizing radiations such as α-particles (9). The high weighting-factor value for α-particles reflects the greater potential per unit absorbed dose of high–linear-energy-transfer, densely ionizing radiations to induce stochastic effects in an organ or tissue (such as cancer and germ-cell, or hereditary, mutations) relative to that of a unit absorbed dose of sparsely ionizing radiations. The equivalent dose is thus defined as follows: Embedded ImageEq. 4 where Embedded Image is the radiation weighting factor for radiation R, and Embedded Image is the contribution of radiation R to the mean absorbed dose to tissue Embedded Image over a time interval τ. The SI unit for equivalent dose is the J kg−1, with the special named unit of sievert. The older unit is the erg g−1 or the special named unit of rem; 1 Sv equals 100 rem, and 1 rem equals 1 cSv (or 10 mSv). Current ICRP-recommended values of Embedded Image, which is a dimensionless quantity, are 1.0 for photons, electrons, positrons, and β-particles and 20 for α-particles (9).

Effective Dose

The effective dose is another radiation-protection quantity derived from the absorbed dose that accounts for both the radiation weighting factor wR and the relative stochastic risk for given organ equivalent doses, accounting for the differences among tissues of the age- and sex-averaged radiogenic risks of cancer induction (applicable to somatic tissues) and germ-cell mutation (applicable to gonadal tissues). Effective dose thus is not a dose metric for a specific individual but rather a population-averaged quantity that may be compared with a radiation protection standard or among different radiation exposures. Numerically, effective dose is the sum of all the weighted equivalent doses for all organs and tissues of the body of a reference anatomic model, whether the body is irradiated uniformly or nonuniformly: Embedded ImageEq. 5 where Embedded Image and Embedded Image are the dose equivalents to target tissue T in the reference male and reference female phantom, respectively, over the dose-integration time interval τ, and wT is a tissue weighting factor defined as the fraction of total stochastic risk associated with individual target tissue T. Values for the tissue weighting factor Embedded Image, a dimensionless quantity, are recommended in ICRP publication 103 (9).

It must be emphasized that assessment of an individual patient’s excess cancer risk associated with a nuclear medicine or other medical imaging procedure based on the effective dose for that procedure in combination with any available cancer risk factors is not appropriate, as the tissue weighting factors wT, as well as the risk factors, are average values not applicable to any individual.

THE COMPUTATIONAL ENGINE—THE DOSE-CALCULATION FORMULAS—OF THE MIRD SCHEMA

The fundamental equations of the MIRD schema, yielding the mean absorbed dose Embedded Image to a target region Embedded Image over an integration period τ (i.e., from time t = 0 to time t = τ) after administration of a radiopharmaceutical for a particular radionuclide in a particular anatomic model (1), are as follows (Table 1 defines the parameters in Eqs. 6–11): Embedded ImageEq. 6 Embedded ImageEq. 7 Embedded ImageEq. 8 whereEmbedded ImageEq. 9 Embedded ImageEq. 10 Embedded ImageEq. 11

As noted in Table 1, the integration time τ is commonly set to infinity (i.e., Embedded Image, yielding the total absorbed dose to target region Embedded Image for complete decay of the administered radiopharmaceutical. As applied to diagnostic radiopharmaceuticals, its traditional application, the MIRD schema implicitly assumes that activity and time-integrated activities are uniformly distributed within source organs and that radiation energy is uniformly deposited within target organs.

Although identical in terms of the calculation performed, Equations 6–8 are made progressively simpler in appearance by combining multiple parameters into various single parameters, particularly with the introduction of the S value (Eqs. 9–11). The ingenuity of the MIRD schema lies in reducing a challenging, seemingly intractable computational task—calculation of the absorbed dose to several irregular target regions (i.e., organs) from the nonuniform and time-varying distribution of a radionuclide among several irregular source regions (i.e., also organs)—to a series of more manageable components. More specifically, the MIRD schema separates the relevant biology from the relevant physics, as most clearly shown in Equation 8: all the biology is combined in the time-integrated activity, Embedded Image, and all the physics in the S value, Embedded Image The S values are, of course, radionuclide- and anatomic model–specific (10), as the energies and frequencies per decay Embedded Image of emitted radiations (11–13) depend on the radionuclide, and the absorbed fractions (Embedded Image depend on the anatomic model (i.e., the sizes, shapes, and separations of the organs) as well as the radionuclide and its emitted radiations (14). Conceptually, the S value Embedded Image is equivalent to the absorbed dose to target region Embedded Image per decay of the radionuclide in source region Embedded Image.

Although perhaps daunting in appearance, Equations 6–8 are conceptually quite simple, as shown when expressed in literal terms:

Figure

Summing the dose contributions above from each source organ rs to the target organ rT over all the source organs of the body then yields the total absorbed dose to target organ rT.

For any given dose calculation, time–activity data and time-integrated activities are typically available for only a limited number of source regions (15). It is important that these include the total body, so that the rest-of-body (also known as the remainder of body) time-integrated activity Embedded Image—and the potentially large rest-of-body dose contribution—may be calculated: Embedded ImageEq. 12 where the total-body time-integrated activity, Embedded Image, is not included in the summation term, Embedded Image The rest-of-body S values may be calculated using the formula provided by Coffey and Watson (16): 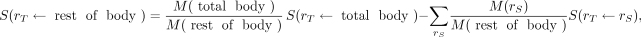Embedded ImageEq. 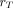13 where S(Embedded Image←rest of body) and S(Embedded Image←total body) are the rest-of-body–to–Embedded Image and total-body–to–Embedded Image S values, Embedded Image are the total-body and rest-of-body masses, respectively; andEmbedded ImageEq. 14

S VALUES AND ANATOMIC MODELS

As noted in the previous section, S values and related quantities (Eqs. 9–11) depend on the particular radionuclide and anatomic model. The relevant radionuclide decay data are available in any number of authoritative sources, such as the MIRD radionuclide data and decay schemes (11,12) and ICRP publication 107 (13); these publications are noteworthy in that they provide tabulations of decay data in a form specifically designed for internal dosimetry. Derivation of S values, on the other hand, is a challenging computational task. Ideally, S values would be computed by Monte Carlo radiation-transport simulations or other computational means using segmented organs in whole-body CT or MR images of each individual patient. Only then would one have truly patient-specific S values. Although this is generally impractical and not done for diagnostic radiopharmaceuticals, this approach is actually being pursued for radiopharmaceutical therapies using certain commercially available software packages (3,17). Even then, however, only a limited number of organs are imaged in a typical partial-body CT or MRI study and incorporated into a patient-specific dose calculation. More commonly, organ-level dosimetry is performed using precomputed tables of radionuclide S values for source-organ/target-organ pairs selected from a series of anatomic computerized models (or phantoms) of age-dependent average individuals. For illustrative purposes, a partial tabulation of S values for 131I in the ICRP voxel-based phantom of the reference adult male is presented in Table 2 (18,19). Such models, or phantoms, may be classified by their respective format type (i.e., mathematic representation) and morphometric fidelity (i.e., patient anatomic specificity), as outlined in Table 3.

View this table:
TABLE 2.

S Values for 131I-Derived from ICRP Voxel-Based Computational Phantom of Reference Adult Male (18)

View this table:
TABLE 3.

Classification of Computational Anatomic Phantoms by Format and Morphometric Category (3)

Average individuals are typically taken to be reference persons defined, for example, by the ICRP (20,21); these include males and females at roughly the 50th percentile for heights and weights at specified ages: the newborn, 1-y-old, 5-y-old, 10-y-old, 15-y-old, and adult. Historically, the MIRD schema has used S values computed using the age-specific stylized computational phantoms of reference individuals developed at the Oak Ridge National Laboratory (ORNL) (Fig. 1A) (22). These computational phantoms include models of organ and body contours based on regular 3-dimensional mathematic topologies (spheres, ellipsoids, cones, and tapered cylinders, for example). The ICRP subsequently developed a family of reference voxel-based phantoms (Fig. 1B) (18,23). These phantoms are ultimately derived from CT image sets of cadavers of actual individuals, and thus, the anatomy is more realistic than that of the ORNL stylized phantoms. Besides having greater anatomic fidelity, the voxel-based ICRP phantoms include a larger number of source and target regions (55 and 42, respectively) than the ORNL phantoms (20 and 20, respectively). A comparison of 131I S values—for selected source and target regions—for the ORNL stylized phantoms and the ICRP voxel-based phantoms of the reference adult male and female is presented graphically in Figure 2 (24). Although yielding reasonably accurate results overall, the modeling of anatomy with simplistic shapes in the ORNL stylized phantoms introduces some inaccuracies in S values as compared with the ICRP voxel-based phantoms. For several source–target pairs, in fact, the differences in S values are up to 10-fold. Modern implementations of the MIRD schema (including the MIRDcalc software (19,25)) generally use the S values for the family of ICRP voxel-based phantoms (18).

FIGURE 1.
FIGURE 1.

(A) Family of stylized reference phantoms from ORNL (22). Each phantom has both male and female sex organs. (B) Family of voxel-based reference phantoms from ICRP (18,23). Total of 12 phantoms are in ICRP reference series. In this figure, only male versions are shown for ages below 15 y. (Reprinted from (3).)

FIGURE 2.
FIGURE 2.

Ratio (median) of 131I S values for ICRP voxel-based phantoms to values for ORNL stylized phantoms for selected source-region/target-region pairs. (Reprinted from (24).)

Among the different format types, polygon mesh-based phantoms perhaps provide the greatest flexibility and anatomic fidelity. The ICRP recently developed mesh-type reference phantoms that address certain shortcomings of the voxel-based reference phantoms (26). Such phantoms can be used, for example, to create posture (e.g., standing, walking, kneeling)-specific anatomic models to elucidate the impact of posture on internal dose estimates (27).

Differences in body size and contour and internal organ anatomy between a reference phantom (regardless of how realistic such a phantom may appear) and an individual patient can potentially introduce sizable errors in estimates of mean organ doses to the patient, mainly because of errors in estimation of the self-dose. The self-dose typically accounts for most of the dose to an organ. To a first approximation, self-dose S values scale inversely with organ mass, consistent with the short range (typically about 1 mm or less in tissue) and the assumption of complete local (i.e., intraorgan) absorption of particulate radiations such as α-particles, β-particles (including positrons), and Auger and conversion electrons. Therefore, an individual’s self-dose S value for a particular organ may be obtained from the respective reference-phantom S value by scaling by the ratio of the phantom-to-individual organ mass (assuming the individual’s organ masses have been measured by, for example, CT or MRI). Recently, more accurate scaling approaches for the photon- as well as the particulate-radiation dose contributions have been developed (28).

TIME–ACTIVITY DATA AND TIME-INTEGRATED ACTIVITIES

Each radiopharmaceutical is, of course, characterized by its own time-dependent biodistribution (expressed, for example, as the activity or activity concentration in the different tissues of the body at different times after administration), and this varies not only across different species but also among different subjects of the same species. The biology-related aspects of internal dosimetry—measurement of time–activity data and their reduction to time-integrated activities—are thus particularly challenging.

Initial human absorbed dose estimates for new radiopharmaceuticals—to satisfy regulatory requirements as well as for ethical considerations—are derived from animal biodistribution studies, typically in mice or rats. Such small-animal models are relatively inexpensive, easy to maintain and handle, and available in sufficiently large numbers to achieve reasonable statistical reliability of measured time–activity data (the methodology for measuring biodistribution data for radiopharmaceuticals in small-animal models is beyond scope of this article). The translation of such data to human anatomic models is problematic, however, and no entirely satisfactory method for doing so has been developed thus far (29,30). The most widely used approach is based on the assumption that a radiopharmaceutical’s body mass–normalized activity concentration (equivalent to the SUV, routinely used to parameterize clinical PET scans) in a particular organ at a particular time after administration is the same among subjects of different body masses, whether subjects of the same species (e.g., patients) or subjects across species (e.g., mice vs. humans) This, in turn, is based on the implicit assumption that the biology of the radiopharmaceutical is identical (except, of course, for statistical variations) across subjects and species and that differences in organ activity concentrations are therefore related exclusively to differences in the radiopharmaceutical’s volume of distribution and therefore, in first order, the total-body mass. These considerations yield the following equation relating the organ activity concentration of a radiopharmaceutical in the human (h) anatomic model to that measured in the animal (a) model (in Eq. 15 and subsequent equations, square brackets are, as usual, used to indicate concentrations): Embedded ImageEq. 15 where [A(rS,t)]h and [A(rS,t)]a are the activity concentrations (in percentage of the injected activity per gram, for example) in source region (i.e., organ) rS at time t after administration in the animal model and the human anatomic model, respectively, and BMa and BMh are the total-body masses of the animal model and the human anatomic model, respectively (3).

After administration of a radiopharmaceutical, the radioactivity is distributed among the tissues of the body and eliminated from the body—simultaneously by a combination of physical decay and biologic processes. Physical decay corresponds to the radioactive decay of the radionuclide in the radiopharmaceutical and, of course, occurs at the same rate regardless of its chemical form and whether the radionuclide is in vivo or ex vivo. Biologic processes reflect the behavior of the radiopharmaceutical in vivo independent of radioactive decay. The combination of the simultaneous processes of physical (i.e., radioactive) decay and biologic clearance yields the so-called effective clearance, which is faster than either physical clearance or biologic clearance alone, as illustrated in Figure 3A. Biologic clearance data are often referred to as decay-corrected, since the time–activity data have been adjusted, or corrected, to eliminate the effect of radioactive decay on the clearance of the radionuclide in the radiopharmaceutical. Effective clearance data are sometimes referred to as non–decay-corrected, since these data include the effect of radioactive decay and thus correspond to the overall clearance of the radionuclide in the radiopharmaceutical. It is effective time–activity data that are ultimately required for radiation dose calculations.

FIGURE 3.
FIGURE 3.

(A) Idealized exponentially decreasing time–activity curves illustrating relationship among physical, biologic, and effective half-times in tissue or organ for administered radiopharmaceutical. Each curve is characterized by clearance constant and corresponding half-time, with effective clearance constant being greater than either physical or biologic clearance constant (Eq. 18) and effective half-time being shorter than either physical or biologic half-time (Eq. 23). (Reprinted from (3).) (B) Actual time–activity curve will be more complex, including rising component at early times after administration as radiopharmaceutical exits blood and enters tissue parenchyma of organ. In many cases, this rising portion of time–activity curve is brief compared with remainder of curve and is therefore ignored in fitting mathematic function to curve for purpose of estimating time-integrated activity. More specifically, although fitting of monotonically decreasing exponential function to organ’s time–activity data will overestimate total time-integrated activity to infinite time (i.e., corresponding to complete decay of administered radionuclide), magnitude of this overestimate will be small for small-molecule radiopharmaceuticals. However, for slowly localizing, large-molecule radiopharmaceuticals such as radiolabeled antibodies, this overestimate of time-integrated activity may be significant. Graphically, total time-integrated activity (i.e., area under curve) for actual time–activity curve (represented by upper left–to–lower right slant-line hatching) will be overestimated by amount corresponding to lower left–to–upper right slant-line hatching.

Once organ and total-body time–activity data have been measured, either preclinically in an animal model or clinically for an individual patient, these data must be reduced to time-integrated activities. This is generally accomplished by fitting a mathematic function to these data—most often, an exponential function—once the measured data have been corrected for radioactive decay to the time of administration of the radiopharmaceutical: Embedded ImageEq. 16 where [A(rS,t)]corrected is the activity concentration in source region (i.e., organ) rS at time t after administration corrected for radioactive decay to the time of administration of the radiopharmaceutical; Embedded Image and Embedded Image are the activity concentration in source region (i.e., organ) rS at time t = 0 (i.e., the time of administration of the radiopharmaceutical) and the biologic (b) clearance constant, respectively, of the jth exponential term; and n is the number of exponential terms (or components) in the fitted function. The corresponding version of this function for the data not corrected for radioactive decay is as follows: Embedded ImageEq. 17 where A(rS,t)]not corrected is the activity concentration in source region (i.e., organ) rS at time t after administration not corrected for radioactive decay to the time of administration of the radiopharmaceutical, and Embedded Image is the effective (e) clearance constant, reflecting the processes of both physical decay and biologic clearance such thatEmbedded ImageEq. 18 where Embedded Image is the physical (p) decay constant of the radionuclide. Integration of Equation 17 to infinite time (i.e., for complete decay of the administered radionuclide) then yields the total time-integrated activity, Embedded Image with mass Embedded Image: Embedded ImageEq. 19

The physical decay constant Embedded Image is related to the physical half-life Embedded Imageof the radionuclide by the following equation: Embedded ImageEq. 20

For the jth exponential component, the biologic clearance constant Embedded Image and effective clearance constant Embedded Image are likewise related to the biologic half-life Embedded Image and the effective half-life Embedded Image, respectively: Embedded ImageEq. 21 Embedded ImageEq. 22 and the effective half-time Embedded Image of the jth exponential component is related to the physical half-time Embedded Image and the biologic half-time Embedded Image of the jth exponential component as follows: Embedded ImageEq. 23

Rearranging Equation 22 to solve for Embedded Image in terms of Embedded Image and substituting that expression into Equation 19 yields a formula for the total time-integrated activity, Embedded Image in terms of Embedded Image: Embedded ImageEq. 24

Actual organ time–activity curves include a rising component at early times after administration as the radiopharmaceutical exits the blood and enters the parenchyma of the organ (as illustrated in Fig. 3B). A mathematic function more complex than a sum of exponential terms (Eqs. 16 and 17) is required for reliable fitting to such data, and the reader is referred to section 5.7.1. (analytic curve fitting) in the 2022 MIRD primer (3) for a review of curve fitting for radiopharmaceutical time–activity data. An alternative approach to curve fitting and analytic integration of complex time–activity data is a numeric approach: connecting consecutive data points by straight-line segments and integrating piecewise by the trapezoidal rule. However, integration by the trapezoidal rule extends only to the final data point. Beyond that point to infinity, the integral is indeterminate by the trapezoidal rule and must be estimated by other means (e.g., assuming, conservatively, elimination of activity beyond the final data point by physical decay only).

Curve-fitting computer programs are widely available. These include commercially available software packages such as Excel (part of the Office suite (Microsoft)), OLINDA/EXM (31) (part of the Hermes Hybrid Viewer Dosimetry Module (Hermes)), PMOD (PMOD Technologies Ltd.), and Prism (GraphPad Software), among many others. Recently, the MIRD committee has developed and will release MIRDfit, an Excel-based fitting and integration program that will be part of and freely downloadable from the MIRDsoft website.

BEYOND ORGAN DOSIMETRY: SUBORGAN, VOXEL-LEVEL, AND CELL-LEVEL DOSIMETRY

As noted, as it is applied to diagnostic radiopharmaceuticals, its traditional application, the MIRD schema implicitly assumes that activity and time-integrated activities are uniformly distributed within source organs and that radiation energy is uniformly deposited within target organs. However, a remarkable strength of the MIRD schema is its generality: by judicious selection of source and target regions, it can be used to calculate the dose to virtually any target region from virtually any source region, from microscopic to macroscopic to whole organs and whole body (32). For several organs, including brain and kidney, suborgan MIRD-schema dosimetry has been developed (33,34). MIRD pamphlet no. 17 (35) introduced voxel S values and extended the MIRD schema to arbitrary macroscopic activity distributions in 3 dimensions for calculation of the resulting macroscopic dose distribution; in this context, the term macroscopic refers to volume elements, or voxels, 3 mm or greater in dimension. And, with the publication of MIRD cellular S factors (36) and the release of the MIRDcell computer program (37–39), the MIRD schema has been extended to cellular and subcellular source and target regions. This applet, freely downloadable from the MIRDsoft website, models the cell-level distribution of radiopharmaceuticals, calculates the distribution of the radiation dose at the cellular and subcellular levels for both isolated cells and clusters of cells using cellular S values, and mathematically models the biologic responses of the radiolabeled and unlabeled cell populations.

ADAPTATION OF THE MIRD SCHEMA TO PATIENT-SPECIFIC AND TUMOR DOSIMETRY

With the ongoing emergence of new and effective radiopharmaceutical therapies such as 177Lu-DOTATATE (Lutathera; Novartis) and 177Lu-vipivotide tetraxetan (Pluvicto; Novartis), there is widespread, and growing, interest in the development of individualized (i.e., patient-specific) radiation dosimetry, including both normal-organ and tumor dosimetry. The tissue doses associated with radiopharmaceutical therapy are much higher than those for diagnostic applications of radiopharmaceuticals, and severe, potentially life-threatening deterministic effects may therefore result. Consequently, optimally balancing tumor (or other target-tissue) and normal-organ radiation doses requires patient-specific dosimetry. The practical implementation of patient-specific dosimetry, as outlined diagrammatically in Figure 4 (40), remains challenging, however. The patient-independent fixed-administered-activity approach (e.g., MBq, MBq/kg of body mass, and MBq/m2 of body surface area), which does not require any kinetic or other patient measurements, remains widely used, therefore. The fixed administered activity for a particular therapeutic radiopharmaceutical is typically established by chemotherapy-like dose-escalation phase 1 or 2 clinical trials. However, several commercial software packages are now available for patient-specific normal-organ and tumor dosimetry in the setting of radiopharmaceutical therapy (17).

FIGURE 4.
FIGURE 4.

General workflow for radiopharmaceutical therapy dosimetry. Test administration may be either pretherapy tracer administration or first cycle of multidose therapy regimen. Calculation of absorbed doses (in terms of either tumor and organ mean doses or dose distributions) or of dose rates D is performed using dose factors (e.g., S values), dose point kernels, or Monte Carlo analysis. Physical dosimetry yields absorbed dose, and bioeffect dosimetry yields dose metrics such as biologically effective dose, equieffective dose, or effective uniform dose (for bioeffect dosimetry). (Reprinted from (40).)

Given its generality, the MIRD schema is adaptable to specific patients, including patients with tumors. As previously noted, patient-specific S values can be computed by Monte Carlo radiation-transport simulations or other computational means using segmented organs in whole-body CT or MR images of each individual patient to yield patient-specific S values. This is being pursued in the setting of radiopharmaceutical therapy. Alternatively, various mathematic formulas may be applied to estimate, approximately, patient-specific organ S values from those of reference anatomic models. A first-order approach for such estimation has been implemented in MIRDcalc (19,25). The OLINDA/EXM computer program also includes an adjustment for organ size for organ-level dosimetry (31). S values for organ sizes that deviate from those of the relevant reference anatomic model (i.e., the closest in total-body mass to that of the reference model) may be adjusted by scaling each organ’s self-dose by the ratio of the patient–to–reference phantom organ mass raised to a constant power. The value of the power was set to −Embedded Image for photon self-dose scaling and −1 for particulate-radiation self-dose scaling. Estimations of cross-dose (i.e., nonself-dose) contributions are unchanged when using adjusted organ masses. MIRDcalc also supports approximate tumor dosimetry by calculating the self-dose to a sphere from time-integrated activity uniformly distributed within the sphere. MIRDcalc allows user selection not only of the spheric and nonspheric volumes but also of composition (i.e., the relative amounts of bone and soft-tissue composing the tumor). Calculation of tumor self-doses is based on S values provided by Olguin et al. (41), with interpolation (i.e., log–log interpolation) or extrapolation of published data points for user-specified volumes.

CONCLUDING REMARKS

The MIRD schema, which originated in the 1960s, has withstood the test of time, and established itself as a worldwide standard for radiopharmaceutical dosimetry. The schema has evolved, and it continues to do so as technology and the field of nuclear medicine have advanced. Stylized reference anatomic models (22) have been replaced by more anatomically realistic voxel-based models (18,23), with a greater number of source and target regions (Fig. 1). Even more anatomically realistic models are becoming available as well (Table 2). Three-dimensional suborgan dosimetry is doable using voxel S values (35), as is cellular and subcellular dosimetry using cell S values and the MIRDcell software (38,39). With ongoing advances in radiopharmaceutical therapy, adaptation of the MIRD schema to patient-specific dosimetry, including tumor dosimetry (41), is well under way, with scaling of reference anatomic-model organ S values to individualized S values and first-order calculation of tumor self-doses (19,25). Further, the MIRD committee is now addressing the radiation biology of radiopharmaceutical therapy (3) (including α-particle therapy (42)) and the methodologies for acquisition of the relevant time–activity data for patient-specific dosimetry (43–45).

Importantly, in addition to its traditional hard-copy resources—the peer-reviewed MIRD pamphlets and associated publications—the MIRD committee has created and is expanding the MIRDsoft website for providing a suite of freely downloadable software tools for radiopharmaceutical dosimetry. MIRDsoft currently hosts MIRDcalc (for organ-level and tumor dosimetry, including such novel features as error propagation) (19,25) and MIRDcell (for not only cellular and subcellular dosimetry but also bioeffect modeling) (38,39). Near-term additions to MIRDsoft will include MIRDfit (for curve fitting, with error propagation, of radiopharmaceutical time–activity data), MIRDy90 (for 90Y-microsphere dosimetry for radioembolic therapy of liver tumors), MIRDrelease (for assessment of the releasability of radiopharmaceutical therapy patients and of the duration of postrelease precautions), and MIRDct (for individualized CT dosimetry).

Like fine wine, the MIRD schema has aged well indeed!

DISCLOSURE

Pat Zanzonico receives, on behalf of the MIRD committee, royalties on sales of the 2022 MIRD primer. No other potential conflict of interest relevant to this article was reported.

Footnotes

  • CE credit: For CE credit, you can access the test for this article, as well as additional JNMT CE tests, online at https://www.snmmilearningcenter.org. Complete the test online no later than June 2027. Your online test will be scored immediately. You may make 3 attempts to pass the test and must answer 80% of the questions correctly to receive 1.0 CEH (Continuing Education Hour) credit. SNMMI members will have their CEH credit added to their VOICE transcript automatically; nonmembers will be able to print out a CE certificate upon successfully completing the test. The online test is free to SNMMI members; nonmembers must pay $15.00 by credit card when logging onto the website to take the test.

  • Published online Mar. 12, 2024.

REFERENCES

  1. 1.↵
    1. Bolch WE,
    2. Eckerman KF,
    3. Sgouros G,
    4. Thomas SR
    . MIRD pamphlet no. 21: a generalized schema for radiopharmaceutical dosimetry—standardization of nomenclature. J Nucl Med. 2009;50:477–484.
    OpenUrlAbstract/FREE Full Text
  2. 2.
    1. Loevinger R,
    2. Budinger T,
    3. Watson E,
    4. et al
    . MIRD Primer for Absorbed Dose Calculations. Revised ed. Society of Nuclear Medicine and Molecular Imaging; 1991.
  3. 3.↵
    MIRD Committee. MIRD Primer 2022: A Complete Guide to Radiopharmaceutical Dosimetry. Society of Nuclear Medicine and Molecular Imaging; 2022.
  4. 4.↵
    1. Zanzonico PB
    . Internal radionuclide radiation dosimetry: a review of basic concepts and recent developments. J Nucl Med. 2000;41:297–308.
    OpenUrlAbstract/FREE Full Text
  5. 5.↵
    Radiation Quantities and Units. International Commission on Radiation Units and Measurements (ICRU) Report 33. International Commission on Radiation Units and Measurements; 1980.
  6. 6.
    SI Units in Radiation Protection and Measurements. National Council on Radiation Protection and Measurements (NCRP) Report 82. National Council on Radiation Protection and Measurements; 1985.
  7. 7.
    1. Harrison JD,
    2. Streffer C
    . The ICRP protection quantities, equivalent and effective dose: their basis and application. Radiat Prot Dosimetry. 2007;127:12–18.
    OpenUrlCrossRefPubMed
  8. 8.↵
    Measurements. Report 85: fundamental quantities and units for ionizing radiation. J ICRU. 2011;11:1–31.
    OpenUrlCrossRefPubMed
  9. 9.↵
    2007 recommendations of the International Commission on Radiological Protection. International Commission on Radiological Protection (ICRP) publication 103. Ann ICRP. 2007;37:1–332.
    OpenUrlCrossRefPubMed
  10. 10.↵
    1. Snyder W,
    2. Ford M,
    3. Warner G,
    4. Watson S
    . “S,” Absorbed Dose Per Unit Cumulated Activity for Selected Radionuclides and Organs. Medical Internal Radiation Dose (MIRD) Pamphlet No 11. Society of Nuclear Medicine and molecular imaging; 1975.
  11. 11.↵
    1. Eckerman KF,
    2. Endo A
    . MIRD: Radionuclide Data and Decay Schemes. 2nd ed. Society of Nuclear Medicine and Molecular Imaging; 1989.
  12. 12.↵
    1. Weber D,
    2. Eckerman K,
    3. Dillman L,
    4. Ryman J
    . MIRD: Radionuclide Data and Decay Schemes. Society of Nuclear Medicine and Molecular Imaging; 1989.
  13. 13.↵
    1. Eckerman K,
    2. Endo A
    . ICRP publication 107. Nuclear decay data for dosimetric calculations. Ann ICRP. 2008;38:7–96.
    OpenUrlPubMed
  14. 14.↵
    1. Snyder WS,
    2. Fisher HL Jr.,
    3. Ford MR,
    4. Warner GG
    . Estimates of absorbed fractions for monoenergetic photon sources uniformly distributed in various organs of a heterogeneous phantom. MIRD pamphlet no 5. J Nucl Med. 1969;10(suppl 3):5–52.
    OpenUrl
  15. 15.↵
    1. Josefsson A,
    2. Siritantikorn K,
    3. Ranka S,
    4. et al
    . Accuracy in dosimetry of diagnostic agents: impact of the number of source tissues used in whole organ S value-based calculations. EJNMMI Res. 2020;10:26.
    OpenUrl
  16. 16.↵
    1. Coffey JL,
    2. Watson EE
    . Calculating dose from remaining body activity: a comparison of two methods. Med Phys. 1979;6:307–308.
    OpenUrlCrossRefPubMed
  17. 17.↵
    1. Capala J,
    2. Graves SA,
    3. Scott A,
    4. et al
    . Dosimetry for radiopharmaceutical therapy: current practices and commercial resources. J Nucl Med. 2021;62(suppl 3):3S–11S.
    OpenUrlAbstract/FREE Full Text
  18. 18.↵
    1. Menzel HG,
    2. Clement C,
    3. DeLuca P
    . ICRP publication 110. Realistic reference phantoms: an ICRP/ICRU joint effort. A report of adult reference computational phantoms. Ann ICRP. 2009;39:1–164.
    OpenUrlPubMed
  19. 19.↵
    1. Kesner AL,
    2. Carter LM,
    3. Ramos JCO,
    4. et al
    . MIRD pamphlet no. 28, part 1: MIRDcalc-A software tool for medical internal radiation dosimetry. J Nucl Med. 2023;64:1117–1124.
    OpenUrlAbstract/FREE Full Text
  20. 20.↵
    Basic anatomical and physiological data for use in radiological protection: the skeleton. A report of a Task Group of Committee 2 of the International Commission on Radiological Protection. Ann ICRP. 1995;25:1–80.
    OpenUrlCrossRefPubMed
  21. 21.↵
    Basic anatomical and physiological data for use in radiological protection: reference values. A report of age- and gender-related differences in the anatomical and physiological characteristics of reference individuals. ICRP publication 89. Ann ICRP. 2002;32:5–265.
    OpenUrlCrossRefPubMed
  22. 22.↵
    1. Cristy M,
    2. Eckerman K
    . Specific Absorbed Fractions of Energy at Various Ages from Internal Photon Sources (I-VII). Oak Ridge National Laboratory Report ORNL/TM-8381/V1-7. National Technical Information Service, Department of Commerce; 1987.
  23. 23.↵
    Bolch WE, Eckerman K, Endo A, et al. ICRP publication 143: paediatric reference computational phantoms. Ann ICRP. 2020;49:5–297.
  24. 24.↵
    1. Lamart S,
    2. Simon SL,
    3. Bouville A,
    4. Moroz BE,
    5. Lee C
    . S values for 131I based on the ICRP adult voxel phantoms. Radiat Prot Dosimetry. 2016;168:92–110.
    OpenUrlCrossRefPubMed
  25. 25.↵
    1. Carter LM,
    2. Ocampo Ramos JC,
    3. Olguin EA,
    4. et al
    . MIRD pamphlet no. 28, part 2: comparative evaluation of MIRDcalc dosimetry software across a compendium of diagnostic radiopharmaceuticals. J Nucl Med. 2023;64:1295–1303.
    OpenUrlAbstract/FREE Full Text
  26. 26.↵
    Kim CH, Yeom YS, Petoussi-Henss N, et al. ICRP publication 143: adult mesh-type reference computational phantoms. Ann ICRP. 2020;49:13–201.
  27. 27.↵
    1. Carter LM,
    2. Bellamy MB,
    3. Choi C,
    4. et al
    . Influence of body posture on internal organ dosimetry: radiocesium exposure modeling using novel posture-dependent mesh computational phantoms. Health Phys. 2023;125:137–146.
    OpenUrl
  28. 28.↵
    1. Wayson MB,
    2. Bolch WE
    . Individualized adjustments to reference phantom internal organ dosimetry-scaling factors given knowledge of patient internal anatomy. Phys Med Biol. 2018;63:085006.
    OpenUrl
  29. 29.↵
    1. Watson E,
    2. Schlafke-Stelson A,
    3. Coffey J,
    4. Cloutier R
    1. Thomas J,
    2. Eberhardt L
    . Can results from animal studies be used to estimate dose or low dose effects in humans? In: Watson E, Schlafke-Stelson A, Coffey J, Cloutier R, eds. Proceedings of the Third International Radiopharmaceutical Dosimetry Symposium. U.S. Department of Health and Human Services; 1981:259–282.
  30. 30.↵
    1. Watson E,
    2. Schlafke-Stelson A,
    3. Coffey J,
    4. Cloutier R
    1. Crawford D,
    2. Richmond C
    . Epistemological considerations in the extrapolation of metabolic data from non-human to humans. In: Watson E, Schlafke-Stelson A, Coffey J, Cloutier R, eds. Proceedings of the Third International Radiopharmaceutical Dosimetry Symposium. U.S. Department of Health and Human Services; 1981:181–197.
  31. 31.↵
    1. Stabin MG,
    2. Sparks RB,
    3. Crowe E
    . OLINDA/EXM: the second-generation personal computer software for internal dose assessment in nuclear medicine. J Nucl Med. 2005;46:1023–1027.
    OpenUrlAbstract/FREE Full Text
  32. 32.↵
    1. Howell RW
    . The MIRD schema: from organ to cellular dimensions. J Nucl Med. 1994;35:531–533.
    OpenUrlFREE Full Text
  33. 33.↵
    1. Bouchet LG,
    2. Bolch WE,
    3. Weber DA,
    4. Atkins HL,
    5. Poston JW Sr.
    . MIRD pamphlet no. 15: radionuclide S values in a revised dosimetric model of the adult head and brain. Medical internal radiation dose. J Nucl Med. 1999;40:62S–101S.
    OpenUrlAbstract/FREE Full Text
  34. 34.↵
    1. Wessels BW,
    2. Konijnenberg MW,
    3. Dale RG,
    4. et al
    . MIRD pamphlet no. 20: the effect of model assumptions on kidney dosimetry and response—implications for radionuclide therapy. J Nucl Med. 2008;49:1884–1899.
    OpenUrlAbstract/FREE Full Text
  35. 35.↵
    1. Bolch WE,
    2. Bouchet LG,
    3. Robertson JS,
    4. et al
    . MIRD pamphlet no. 17: the dosimetry of nonuniform activity distributions—radionuclide S values at the voxel level. Medical Internal Radiation Dose Committee. J Nucl Med. 1999;40:11S–36S.
    OpenUrlAbstract/FREE Full Text
  36. 36.↵
    1. Goddu S,
    2. Howell R,
    3. Bouchet L,
    4. et al
    . MIRD Cellular S Factors: Self-Absorbed Dose per Unit Cumulated Activity for Selected Radionuclides and Monoenergetic Electrons and Alpha Particle Emitters Incorporated into Different Cell Compartments. Society of Nuclear Medicine and Molecular Imaging; 1997.
  37. 37.↵
    1. Katugampola S,
    2. Wang J,
    3. Prasad A,
    4. Sofou S,
    5. Howell RW
    . Predicting response of micrometastases with MIRDcell V3: proof of principle with 225Ac-DOTA encapsulating liposomes that produce different activity distributions in tumor spheroids. Eur J Nucl Med Mol Imaging. 2022;49:3989–3999.
    OpenUrl
  38. 38.↵
    1. Katugampola S,
    2. Wang J,
    3. Rosen A,
    4. Howell RW
    ; SNMMI MIRD committee. MIRD pamphlet no. 27: MIRDcell V3, a revised software tool for multicellular dosimetry and bioeffect modeling. J Nucl Med. 2022;63:1441–1449.
    OpenUrlAbstract/FREE Full Text
  39. 39.↵
    1. Vaziri B,
    2. Wu H,
    3. Dhawan AP,
    4. Du P,
    5. Howell RW
    ; SNMMI MIRD committee. MIRD pamphlet no. 25: MIRDcell V2.0 software tool for dosimetric analysis of biologic response of multicellular populations. J Nucl Med. 2014;55:1557–1564.
    OpenUrlAbstract/FREE Full Text
  40. 40.↵
    1. O’Donoghue J,
    2. Zanzonico P,
    3. Humm J,
    4. Kesner A
    . Dosimetry in radiopharmaceutical therapy. J Nucl Med. 2022;63:1467–1474.
    OpenUrlAbstract/FREE Full Text
  41. 41.↵
    1. Olguin E,
    2. President B,
    3. Ghaly M,
    4. Frey E,
    5. Sgouros G,
    6. Bolch WE
    . Specific absorbed fractions and radionuclide S-values for tumors of varying size and composition. Phys Med Biol. 2020;65:235015.
    OpenUrl
  42. 42.↵
    1. Sgouros G,
    2. Roeske JC,
    3. McDevitt MR,
    4. et al
    . MIRD pamphlet no. 22 (abridged): radiobiology and dosimetry of alpha-particle emitters for targeted radionuclide therapy. J Nucl Med. 2010;51:311–328.
    OpenUrlAbstract/FREE Full Text
  43. 43.↵
    1. Dewaraja YK,
    2. Frey EC,
    3. Sgouros G,
    4. et al
    . MIRD pamphlet no. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy. J Nucl Med. 2012;53:1310–1325.
    OpenUrlAbstract/FREE Full Text
  44. 44.
    1. Dewaraja YK,
    2. Ljungberg M,
    3. Green AJ,
    4. et al
    . MIRD pamphlet no. 24: guidelines for quantitative 131I SPECT in dosimetry applications. J Nucl Med. 2013;54:2182–2188.
    OpenUrlAbstract/FREE Full Text
  45. 45.↵
    1. Ljungberg M,
    2. Celler A,
    3. Konijnenberg MW,
    4. et al
    . MIRD pamphlet no. 26: joint EANM/MIRD guidelines for quantitative 177Lu SPECT applied for dosimetry of radiopharmaceutical therapy. J Nucl Med. 2016;57:151–162.
    OpenUrlAbstract/FREE Full Text
  • Received for publication September 20, 2023.
  • Revision received January 20, 2024.
View Abstract
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Keywords